Skip to main content
Springer Nature Link
Log in

Operator Splittings, Bregman Methods and Frame Shrinkage in Image Processing

  • Published:
International Journal of Computer Vision Aims and scope Submit manuscript

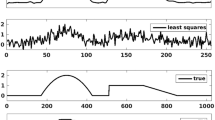
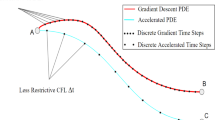
Abstract

We examine the underlying structure of popular algorithms for variational methods used in image processing. We focus here on operator splittings and Bregman methods based on a unified approach via fixed point iterations and averaged operators. In particular, the recently proposed alternating split Bregman method can be interpreted from different points of view—as a Bregman, as an augmented Lagrangian and as a Douglas-Rachford splitting algorithm which is a classical operator splitting method. We also study similarities between this method and the forward-backward splitting method when applied to two frequently used models for image denoising which employ a Besov-norm and a total variation regularization term, respectively. In the first setting, we show that for a discretization based on Parseval frames the gradient descent reprojection and the alternating split Bregman algorithm are equivalent and turn out to be a frame shrinkage method. For the total variation regularizer, we also present a numerical comparison with multistep methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Aubin, J. P., & Frankowska, H. (2009). Set-valued analysis. Boston: Birkhäuser.

    MATH  Google Scholar 

  • Aujol, J. F. (2009). Some first-order algorithms for total variation based image restoration. Journal of Mathematical Imaging and Vision, 34(3), 307–327.

    Article  MathSciNet  Google Scholar 

  • Barzilai, J., & Borwein, J. M. (1988). Two-point step size gradient methods. IMA Journal of Numerical Analysis, 8, 141–148.

    Article  MathSciNet  MATH  Google Scholar 

  • Bauschke, H. H., & Borwein, J. M. (1996). On projection algorithms for solving convex feasibility problems. SIAM Review, 38(3), 367–426.

    Article  MathSciNet  MATH  Google Scholar 

  • Bechler, P., DeVore, R., Kamont, A., Petrova, G., & Wojtaszczyk, P. (2006). Greedy wavelet projections are bounded on BV. Transactions of the American Mathematical Society, 359(2), 619–635.

    Article  MathSciNet  Google Scholar 

  • Beck, A., & Teboulle, M. (2009a). Fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2(1), 183–202.

    Article  MathSciNet  MATH  Google Scholar 

  • Beck, A., & Teboulle, M. (2009b). Fast gradient-based algorithms for constrained total variation image denoising and deblurring. IEEE Transactions on Image Processing, 18(11), 2419–2434.

    Article  MathSciNet  Google Scholar 

  • Bioucas-Dias, J., & Figueiredo, M. (2009). Total variation restoration of speckled images using a split-Bregman algorithm. In Proceedings of the international conference on image processing, ICIP 2009, Cairo, Egypt (pp. 3717–3720). New York: IEEE.

    Google Scholar 

  • Bonnans, J. F., & Shapiro, A. (2000). Springer series in operations research : Vol. 7. Perturbation analysis of optimization problems. Berlin: Springer.

    MATH  Google Scholar 

  • Borwein, J. M., & Zhu, Q. J. (2005). Techniques of variational analysis. New York: Springer.

    MATH  Google Scholar 

  • Borwein, J. M., & Zhu, Q. J. (2006). Variational methods in convex analysis. Journal of Global Optimization, 35(2), 197–213.

    Article  MathSciNet  MATH  Google Scholar 

  • Bregman, L. M. (1967). The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Computational Mathematics and Mathematical Physics, 7(3), 200–217.

    Article  Google Scholar 

  • Browder, F. E., & Petryshyn, W. V. (1966). The solution by iteration of nonlinear functional equations in Banach spaces. Bulletin of the American Mathematical Society, 72, 571–575.

    Article  MathSciNet  MATH  Google Scholar 

  • Buades, A., Coll, B., & Morel, J. M. (2008). Nonlocal image and movie denoising. International Journal of Computer Vision, 76(2), 123–139.

    Article  Google Scholar 

  • Byrne, C. (2004). A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Problems, 20, 103–120.

    Article  MathSciNet  MATH  Google Scholar 

  • Cai, J. F., Chan, R. H., & Shen, Z. (2008). A framelet-based image inpainting algorithm. Applied and Computational Harmonic Analysis, 24, 131–149.

    Article  MathSciNet  MATH  Google Scholar 

  • Cai, J. F., Osher, S., & Shen, Z. (2009). Split Bregman methods and frame based image restoration (Technical report). UCLA Computational and Applied Mathematics.

  • Censor, Y., & Lent, A. (1981). An iterative row-action method for interval convex programming. Journal of Optimization Theory and Applications, 34(3), 321–353.

    Article  MathSciNet  MATH  Google Scholar 

  • Censor, Y., & Zenios, S. A. (1992). Proximal minimization algorithm with D-functions. Journal of Optimization Theory and Applications, 73(3), 451–464.

    Article  MathSciNet  MATH  Google Scholar 

  • Censor, Y., & Zenios, S. A. (1997). Parallel optimization: Theory, algorithms, and applications. New York: Oxford University Press.

    MATH  Google Scholar 

  • Chambolle, A. (2004). An algorithm for total variation minimization and applications. Journal of Mathematical Imaging and Vision, 20(1–2), 89–97.

    MathSciNet  Google Scholar 

  • Chambolle, A. (2005). Total variation minimization and a class of binary MRF models. In A. Rangarajan, B. C. Vemuri, & A. L. Yuille (Eds.), Lecture notes in computer science : Vol. 3757. Energy minimization methods in computer vision and pattern recognition, EMMCVPR (pp. 136–152). Berlin: Springer.

    Chapter  Google Scholar 

  • Chan, R. H., Setzer, S., & Steidl, G. (2008). Inpainting by flexible Haar-wavelet shrinkage. SIAM Journal on Imaging Science, 1, 273–293.

    Article  MathSciNet  MATH  Google Scholar 

  • Cohen, A., DeVore, R., Petrushev, P., & Xu, H. (1999). Nonlinear approximation and the space BV(ℝ2). American Journal of Mathematics, 121, 587–628.

    Article  MathSciNet  MATH  Google Scholar 

  • Combettes, P. L. (2004). Solving monotone inclusions via compositions of nonexpansive averaged operators. Optimization, 53(5–6), 475–504.

    Article  MathSciNet  MATH  Google Scholar 

  • Combettes, P. L., & Pesquet, J. C. (2007). A Douglas-Rachford splitting approach to nonsmooth convex variational signal recovery. IEEE Journal of Selected Topics in Signal Processing, 1(4), 564–574.

    Article  Google Scholar 

  • Combettes, P. L., & Wajs, V. R. (2005). Signal recovery by proximal forward-backward splitting. Multiscale Modelling & Simulation, 4, 1168–1200.

    Article  MathSciNet  MATH  Google Scholar 

  • Daubechies, I., Han, B., Ron, A., & Shen, Z. (2003). Framelets: MRA-based construction of wavelet frames. Applied and Computational Harmonic Analysis, 14, 1–46.

    Article  MathSciNet  MATH  Google Scholar 

  • DeVore, R. A., & Lucier B. J. (1992). Fast wavelet techniques for near-optimal image processing. In IEEE MILCOM ’92 conf. rec. (Vol. 3, pp. 1129–1135). San Diego: IEEE Press.

    Chapter  Google Scholar 

  • Dong, B., & Shen, Z. (2007). Pseudo-splines, wavelets and framelets. Applied and Computational Harmonic Analysis, 22, 78–104.

    Article  MathSciNet  MATH  Google Scholar 

  • Douglas, J., & Rachford, H. H. (1956). On the numerical solution of heat conduction problems in two and three space variables. Transactions of the American Mathematical Society, 82(2), 421–439.

    MathSciNet  MATH  Google Scholar 

  • Eckstein, J. (1989). Splitting methods for monotone operators with applications to parallel optimization. PhD thesis, Massachusetts Institute of Technology.

  • Eckstein, J. (1993). Nonlinear proximal point algorithms using Bregman functions, with applications to convex programming. Mathematics of Operations Research, 18(1), 202–226.

    Article  MathSciNet  MATH  Google Scholar 

  • Eckstein, J., & Bertsekas, D. P. (1992). On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming, 55, 293–318.

    Article  MathSciNet  MATH  Google Scholar 

  • Ekeland, I., & Temam, R. (1976). Convex analysis and variational problems. Amsterdam: North-Holland.

    MATH  Google Scholar 

  • Esser, E. (2009). Applications of Lagrangian-based alternating direction methods and connections to split Bregman (Technical report). UCLA Computational and Applied Mathematics.

  • Esser, E., Zhang, X., & Chan, T. F. (2009). A general framework for a class of first order primal-dual algorithms for TV minimization (Technical report). UCLA Computational and Applied Mathematics.

  • Figueiredo, M., & Bioucas-Dias, J. (2009). Deconvolution of Poissonian images using variable splitting and augmented Lagrangian optimization. In IEEE workshop on statistical signal processing. Cardiff.

  • Frick, K. (2008). The augmented Lagrangian method and associated evolution equations. PhD thesis.

  • Gabay, D. (1983). Applications of the method of multipliers to variational inequalities. In M. Fortin & R. Glowinski (Eds.), Studies in mathematics and its applications : Vol. 15. Augmented Lagrangian methods: Applications to the numerical solution of boundary-value problems (pp. 299–331). Amsterdam: North-Holland. Chap. 9.

    Chapter  Google Scholar 

  • Gabay, D., & Mercier, B. (1976). A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Computers & Mathematics with Applications, 2, 17–40.

    Article  MATH  Google Scholar 

  • Gilboa, G., & Osher, S. (2008). Nonlocal operators with applications to image processing. Multiscale Modelling & Simulation, 7(3), 1005–1028.

    Article  MathSciNet  MATH  Google Scholar 

  • Gilboa, G., Darbon, J., Osher, S., & Chan, T. F. (2006). Nonlocal convex functionals for image regularization (UCLA CAM Report 06-57).

  • Glowinski, R., & Marroco, A. (1975). Sur l’approximation par éléments finis d’ordre un, et la résolution, par pénalisation-dualité d’une classe de problèmes de Dirichlet non linéaires. Revue Française d’Automatique, Informatique, Recherche Opérationnelle Analyse Numérique, 9(2), 41–76.

    Google Scholar 

  • Goldstein, T., & Osher, S. (2009). The split Bregman method for L1-regularized problems. SIAM Journal on Imaging Sciences, 2(2), 323–343.

    Article  MathSciNet  MATH  Google Scholar 

  • Goldstein, T., Bresson, X., & Osher, S. (2009). Geometric applications of the split Bregman method: Segmentation and surface reconstruction (Technical report). UCLA Computational and Applied Mathematics.

  • Hestenes, M. R. (1969). Multiplier and gradient methods. Journal of Optimization Theory and Applications, 4, 303–320.

    Article  MathSciNet  MATH  Google Scholar 

  • Iusem, A. N. (1999). Augmented Lagrangian methods and proximal point methods for convex optimization. Investigación Operativa, 8, 11–49.

    Google Scholar 

  • Kindermann, S., Osher, S., & Jones, P. W. (2005). Deblurring and denoising of images by nonlocal functionals. Multiscale Modelling & Simulation, 4(4), 1091–1115.

    Article  MathSciNet  MATH  Google Scholar 

  • Kiwiel, K. C. (1997). Proximal minimization methods with generalized Bregman functions. SIAM Journal on Control and Optimization, 35(4), 1142–1168.

    Article  MathSciNet  MATH  Google Scholar 

  • Krasnoselskii, M. A. (1955). Two observations about the method of successive approximations. Uspekhi Matematicheskikh Nauk, 10, 123–127 (in Russian).

    MathSciNet  Google Scholar 

  • Levenberg, K. (1944). A method for the solution of certain problems in least squares. Quarterly of Applied Mathematics, 2, 164–168.

    MathSciNet  MATH  Google Scholar 

  • Lions, P. L., & Mercier, B. (1979). Splitting algorithms for the sum of two nonlinear operators. SIAM Journal on Numerical Analysis, 16(6), 964–979.

    Article  MathSciNet  MATH  Google Scholar 

  • Mann, W. R. (1953). Mean value methods in iteration. Proceedings of the American Mathematical Society, 16(4), 506–510.

    Article  Google Scholar 

  • Marquardt, D. (1963). An algorithm for least-squares estimation of nonlinear parameters. SIAM Journal of Applied Mathematics, 11, 431–441.

    Article  MathSciNet  MATH  Google Scholar 

  • Moreau, J. J. (1965). Proximité et dualité dans un espace hilbertien. Bulletin de la Societé Mathématique de France, 93, 273–299.

    MathSciNet  MATH  Google Scholar 

  • Mrázek, P., & Weickert, J. (2003). Rotationally invariant wavelet shrinkage. In B. Michaelis & G. Krell (Eds.), Pattern recognition (Vol. 2781, pp. 156–163). Berlin: Springer.

    Chapter  Google Scholar 

  • Nesterov, Y. E. (1983). A method of solving a convex programming problem with convergence rate O(1/k 2). Soviet Mathematics Doklady, 27(2), 372–376.

    MATH  Google Scholar 

  • Nesterov, Y. E. (2005). Smooth minimization of non-smooth functions. Mathematical Programming, 103, 127–152.

    Article  MathSciNet  MATH  Google Scholar 

  • Opial, Z. (1967). Weak convergence of a sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society, 73, 591–597.

    Article  MathSciNet  MATH  Google Scholar 

  • Osher, S., Burger, M., Goldfarb, D., Xu, J., & Yin, W. (2005). An iterative regularization method for the total variation based image restoration. Multiscale Modeling & Simulation, 4, 460–489.

    Article  MathSciNet  MATH  Google Scholar 

  • Passty, G. B. (1979). Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. Journal of Mathematical Analysis and Applications, 72, 383–390.

    Article  MathSciNet  MATH  Google Scholar 

  • Powell, M. J. D. (1969). A method for nonlinear constraints in minimization problems. London: Academic Press.

    Google Scholar 

  • Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.

    MATH  Google Scholar 

  • Rockafellar, R. T. (1976). Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Mathematics of Operations Research, 1(2), 97–116.

    Article  MathSciNet  MATH  Google Scholar 

  • Ron, A., & Shen, Z. (1997). Affine systems in L 2(ℝd): The analysis of the analysis operator. Journal of Functional Analysis, 148, 408–447.

    Article  MathSciNet  MATH  Google Scholar 

  • Rudin, L. I., Osher, S., & Fatemi, E. (1992). Nonlinear total variation based noise removal algorithms. Physica D, 60, 259–268.

    Article  MATH  Google Scholar 

  • Schäfer, H. (1957). Über die Methode sukzessiver Approximationen. Jahresbericht der Deutschen Mathematiker-Vereinigung, 59, 131–140.

    MathSciNet  MATH  Google Scholar 

  • Setzer, S. (2009a). Split Bregman algorithm, Douglas-Rachford splitting and frame shrinkage. In A. Lie, M. Lysaker, K. Morken, & X. C. Tai (Eds.), Lecture notes in computer science : Vol. 5567. Second international conference on scale space methods and variational methods in computer vision, SSVM 2009, Proceedings (pp. 464–476). Voss, Norway, June 1–5, 2009. Berlin: Springer.

    Chapter  Google Scholar 

  • Setzer, S. (2009b). Splitting methods in image processing. PhD thesis, University of Mannheim.

  • Setzer, S., Steidl, G., & Teuber, T. (2010). Deblurring Poissonian images by split Bregman methods. Journal of Visual Communication and Image Representation, 21(3), 193–199.

    Article  MathSciNet  Google Scholar 

  • Steidl, G., & Teuber, T. (2010). Removing multiplicative noise by Douglas-Rachford splitting methods. International Journal of Mathematical Imaging and Vision, 36(2), 168–184.

    Article  Google Scholar 

  • Tai, X. C., & Wu, C. (2009). Augmented Lagrangian method, dual methods and split Bregman iteration for ROF model. In A. Lie, M. Lysaker, K. Morken, & X. C. Tai (Eds.), Lecture notes in computer science : Vol. 5567. Second international conference on scale space methods and variational methods in computer vision, SSVM 2009, Proceedings (pp. 502–513). Voss, Norway, June 1–5, 2009. Berlin: Springer.

    Chapter  Google Scholar 

  • Tseng, P. (1991). Applications of a splitting algorithm to decomposition in convex programming and variational inequalities. SIAM Journal on Control and Optimization, 29, 119–138.

    Article  MathSciNet  MATH  Google Scholar 

  • Wang, Y., Yang, J., Yin, W., & Zhang, Y. (2008). A new alternating minimization algorithm for total variation image reconstruction. SIAM Journal on Imaging Sciences, 1(3), 248–272.

    Article  MathSciNet  MATH  Google Scholar 

  • Weiss, P., Blanc-Féraud, L., & Aubert, G. (2009). Efficient schemes for total variation minimization under constraints in image processing. SIAM Journal on Scientific Computing, 31(3), 2047–2080.

    Article  MathSciNet  MATH  Google Scholar 

  • Welk, M., Steidl, G., & Weickert, J. (2008). Locally analytic schemes: A link between diffusion filtering and wavelet shrinkage. Applied and Computational Harmonic Analysis, 24, 195–224.

    Article  MathSciNet  MATH  Google Scholar 

  • Yin, W., Osher, S., Goldfarb, D., & Darbon, J. (2008). Bregman iterative algorithms for ℓ 1-minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences, 1(1), 143–168.

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu, M. (2008). Fast numerical algorithms for total variation based image restoration. PhD thesis, University of California, Los Angeles, USA.

  • Zhu, M., & Chan, T. F. (2008). An efficient primal-dual hybrid gradient algorithm for total variation image restauration (Technical report). UCLA Computational and Applied Mathematics.

Download references

Author information

Authors and Affiliations

  1. University of Mannheim, Mannheim, Germany

    Simon Setzer

Authors
  1. Simon Setzer
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Simon Setzer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Setzer, S. Operator Splittings, Bregman Methods and Frame Shrinkage in Image Processing. Int J Comput Vis 92, 265–280 (2011). https://doi.org/10.1007/s11263-010-0357-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11263-010-0357-3

Keywords