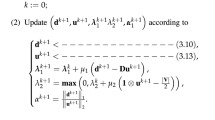Enhanced Balanced Min Cut

Abstract

Spectral clustering is a hot topic and many spectral clustering algorithms have been proposed. These algorithms usually solve the discrete cluster indicator matrix by relaxing the original problems, obtaining the continuous solution and finally obtaining a discrete solution that is close to the continuous solution. However, such methods often result in a non-optimal solution to the original problem since the different steps solve different problems. In this paper, we propose a novel spectral clustering method, named as Enhanced Balanced Min Cut (EBMC). In the new method, a new normalized cut model is proposed, in which a set of balance parameters are learned to capture the differences among different clusters. An iterative method with proved convergence is used to effectively solve the new model without eigendecomposition. Theoretical analysis reveals the connection between EBMC and the classical normalized cut. Extensive experimental results show the effectiveness and efficiency of our approach in comparison with the state-of-the-art methods.

Appendices

A Proof of Theorem 1

Proof

Let $\mathbf {u}\in \mathbb {R}^{c\times 1}$ be a column vector where $u_j=\sum _{i=1}^{n}y_{ij}$ and $\sum _{j=1}^{c}u_j=n$. Let $\mathbf {v}\in \mathbb {R}^{\times 1}$ be a constant column vector where $v_j=\frac{1}{c}$. According to the Cauchy-Schwarz inequality, we have $|<\mathbf {u},\mathbf {v}>|^2\le \left\| {\mathbf {u}}\right\| _{2}^{2}\left\| {\mathbf {v}}\right\| _{2}^{2}$ which indicates that

$$\begin{aligned} \sum _{j=1}^{c}u_j^2\ge \frac{n^2}{c} \end{aligned}$$

(30)

and the inequality hold when $u_j=\frac{n}{c}$ for $\forall j\in [1,c]$. Therefore, $\left\| {\mathbf {Y}}\right\| _b$ arrives its minimum when $\sum _{i=1}^{n}f_{il}=\frac{n}{c}$ if $\frac{n}{c}$ is an integer, or $\sum _{i=1}^{n}f_{il}=\{\lfloor \frac{n}{c}\rfloor ,\lceil \frac{n}{c}\rceil \}$ otherwise ($l\in [1,c]$). Therefore, solving $min_{\mathbf {Y}}\left\| {\mathbf {Y}}\right\| _b$ results in the most balanced partition. $\square$

B Proof of Theorem 2

Proof

Problem (12) can be rewritten as

$$\begin{aligned} \min _{\mathbf {Y}\in \Psi ^{n\times c}, {\mathbf {S}}}\Vert \mathbf {A}-\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\Vert ^{2}_{F}\Leftrightarrow & {} \max _{\mathbf {Y}\in \Psi ^{n\times c},{\mathbf {S}}}2Tr\left( {\mathbf {S}}\mathbf {Y}^{T}\mathbf {A}\mathbf {Y}\right) \nonumber \\&-Tr\left( \mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\right) \end{aligned}$$

(31)

$Tr(\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T})$ can be rewritten as

$$\begin{aligned} \begin{aligned} Tr\left( \mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\right) =\sum _{i=1}^{n}\sum _{j=1}^{n}\sum _{l=1}^{c}\sum _{t=1}^{c}y_{il}s_{ll}y_{jl}y_{jt}s_{tt}y_{it} \end{aligned} \end{aligned}$$

(32)

Since $\mathbf {Y}\in \Psi ^{n\times c}$ is a cluster indicator matrix, we know that $y_{il}y_{it}=1$ if and only if $l=t$, $y^{2}_{il}=y_{il}$, and $y^{2}_{jl}=y_{jl}$. Thus, Eq. (32) can be rewritten as

$$\begin{aligned} Tr\left( \mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\right)= & {} \sum _{i=1}^{n}\sum _{j=1}^{n}\sum _{l=1}^{c}y_{il}s^{2}_{ll}y_{jl}\nonumber \\= & {} \sum _{l=1}^{c}s^{2}_{ll}\left( \sum _{j=1}^{n}y_{il}\right) ^{2}\nonumber \\= & {} Tr\left( {\mathbf {S}}^{2}\mathbf {Y}^{T}{\mathbf {1}}{\mathbf {1}}^{T}\mathbf {Y}\right) \end{aligned}$$

(33)

Therefore, we have

$$\begin{aligned} \begin{aligned}&\max _{\mathbf {Y}\in \Psi ^{n\times c},{\mathbf {S}}}2Tr({\mathbf {S}}\mathbf {Y}^{T}\mathbf {A}\mathbf {Y})-Tr(\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T}\mathbf {Y}{\mathbf {S}}\mathbf {Y}^{T})\\&\quad \Leftrightarrow \max _{\mathbf {Y}\in \Psi ^{n\times c},{\mathbf {S}}}2Tr({\mathbf {S}}\mathbf {Y}^{T}\mathbf {A}\mathbf {Y})-Tr({\mathbf {S}}^{2}\mathbf {Y}^{T}{\mathbf {1}}{\mathbf {1}}^{T}\mathbf {Y})\\&\quad \Leftrightarrow \max _{\mathbf {Y}\in \Psi ^{n\times c},{\mathbf {S}}}\sum _{l=1}^{c}{\mathbf {y}}_{l}^{T}(2s_{ll}\mathbf {A}-s_{ll}^{2}{\mathbf {1}}{\mathbf {1}}^{T}){\mathbf {y}}_{l} \end{aligned} \end{aligned}$$

(34)

which completes the proof. $\square$

C Proof of Theorem 3

Denote the objective function of EBMC in Eq. (13) as $\mathcal {P}({\mathbf {S}},\mathbf {Y})$, and the optimal solution of ${\mathbf {S}}$ and $\mathbf {Y}$ in the t-th and $(t+1)$-th iteration as ${\mathbf {S}}_{t}$, $\mathbf {Y}_{t}$ and ${\mathbf {S}}_{t+1}$, $\mathbf {Y}_{t+1}$. Before giving the proof of Theorem 3, we first give the following lemmas.

Lemma 1

If $\{{\mathbf {M}}^{(1)},\ldots ,{\mathbf {M}}^{(c)}\}$ are all positive semi-definite matrices in the t-th iteration, the following inequation holds

$$\begin{aligned} \begin{aligned} \mathcal {P}({\mathbf {S}}_{t},\mathbf {Y}_{t+1})\ge \mathcal {P}({\mathbf {S}}_{t},\mathbf {Y}_{t})+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{2}^{2} \end{aligned} \end{aligned}$$

(35)

Proof

Denote $\mathbf {Y}$ in the t-th and $(t+1)$-th iterations as $\mathbf {Y}_{t}$ and $\mathbf {Y}_{t+1}$ and ${\mathbf {S}}.$ in the t-th and $(t+1)$-th iterations as ${\mathbf {S}}_{t}$ and ${\mathbf {S}}_{t+1}$, respectively. Since $\mathbf {Y}_{t+1}$ is the optimal solution to problem (16), we have

$$\begin{aligned} \begin{aligned}&\sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {M}}^{(l)})_{t}({\mathbf {y}}_{l})_{t}-\frac{\eta }{2}\left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2}\\&\quad \ge \sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t}({\mathbf {M}}^{(l)})_{t}({\mathbf {y}}_{l})_{t} \end{aligned} \end{aligned}$$

(36)

Since the matrix $({\mathbf {M}}^{(l)})_{t}$ is positive semi-definite, we can rewrite $({\mathbf {M}}^{(l)})_{t}=({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}$ via Cholesky factorization. Then Eq. (36) can be rewritten as

$$\begin{aligned} \begin{aligned}&\sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t+1}-\frac{\eta }{2}\left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2}\\&\quad \ge \sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})^{T}_{t} \end{aligned} \end{aligned}$$

(37)

The inequation $\left\| {{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t+1}-{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t}}\right\| _{F}^{2}\ge 0$ can be rewritten as

$$\begin{aligned} \begin{aligned}&({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t+1}-2({\mathbf {y}}_{l})_{t+1}^{T}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t}\\&\quad +({\mathbf {y}}_{l})^{T}_{t}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t}\ge 0 \end{aligned} \end{aligned}$$

(38)

Summarizing Eq. (38) over all l gives

$$\begin{aligned}&\sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t+1}\nonumber \\&\quad -\,2\sum _{l=1}^{c}({\mathbf {y}}_{l})_{t+1}^{T}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t}\nonumber \\&\quad +\sum _{l=1}^{c}({\mathbf {y}}_{l})_{t}^{T}({\mathbf {Q}}^{(l)}_{B})^{T}{\mathbf {Q}}^{(l)}_{B}({\mathbf {y}}_{l})_{t}\ge 0 \end{aligned}$$

(39)

Multiplying Eq. (37) by 2 and summing over it and Eq. (39) gives

$$\begin{aligned} \begin{aligned}&\sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {Q}}^{(l)}_{B})^{T}({\mathbf {Q}}^{(l)}_{B})({\mathbf {y}}_{l})_{t+1}\\&\quad \ge \sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t}({\mathbf {Q}}^{(l)}_{B})^{T}({\mathbf {Q}}^{(l)}_{B})({\mathbf {y}}_{l})_{t}+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2} \end{aligned} \end{aligned}$$

(40)

which equals to

$$\begin{aligned} \begin{aligned}&\sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t+1}({\mathbf {M}}^{(l)})_{t}({\mathbf {y}}_{l})_{t+1}\\&\quad \ge \sum _{l=1}^{c}({\mathbf {y}}_{l})^{T}_{t}({\mathbf {M}}^{(l)})_{t}({\mathbf {y}}_{t})_{l}+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2} \end{aligned} \end{aligned}$$

(41)

According to the definition of ${\mathbf {M}}^{(l)}$ in Eq. (17), Eq. (41) can be further rewritten as

$$\begin{aligned} \begin{aligned}&2Tr({\mathbf {S}}_{t}(\mathbf {Y})_{t+1}^{T}\mathbf {A}\mathbf {Y}_{t+1})-Tr(({\mathbf {S}})_{t}^{2}(\mathbf {Y})_{t+1}^{T}{\mathbf {1}}{\mathbf {1}}^{T}\mathbf {Y}_{t+1})\\&\quad \ge 2Tr({\mathbf {S}}_{t}(\mathbf {Y})_{t}^{T}\mathbf {A}\mathbf {Y}_{t})\\&\qquad -Tr(({\mathbf {S}})_{t}^{2}(\mathbf {Y})_{t}^{T}{\mathbf {1}}{\mathbf {1}}^{T}\mathbf {Y}_{t})+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2} \end{aligned} \end{aligned}$$

(42)

which equals to

$$\begin{aligned} \begin{aligned} \mathcal {P}({\mathbf {S}}_{t},\mathbf {Y}_{t+1})\ge \mathcal {P}({\mathbf {S}}_{t},\mathbf {Y}_{t})+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{F}^{2} \end{aligned} \end{aligned}$$

(43)

$\square$

Since ${\mathbf {S}}$ is the optimal solution to problem (19) and according to Theorem 1, we can verify the following lemma:

Lemma 2

If $\{{\mathbf {M}}^{(1)},\ldots ,{\mathbf {M}}^{(c)}\}$ are all positive semi-definite matrices in the t-th iteration, $\mathcal {P}({\mathbf {S}}_{t+1},\mathbf {Y}_{t+1})\ge \mathcal {P}({\mathbf {S}}_{t},\mathbf {Y}_{t})+\eta \left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| _{2}^{2}$.

In the following analysis, we omit ${\mathbf {S}}_{t+1}$ in $\mathcal {P}({\mathbf {S}}_{t+1},\mathbf {Y}_{t+1})$ for simplification and give the following important lemma.

Lemma 3

Suppose that $\{{\mathbf {M}}^{(1)},\ldots ,{\mathbf {M}}^{(c)}\}$ are all positive semi-definite matrices after the r-th iteration. If we take $\mathbf {Y}$ as random variable and $\mathbb {E}[\left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| ]$ is the expectation of $\mathbf {Y}_{t+1}-\mathbf {Y}_{t}$ where t is the number of iterations, it holds that $\lim _{t\rightarrow \infty }\mathbb {E}[\left\| {\mathbf {Y}_{t+1}-\mathbf {Y}_{t}}\right\| ]=0$.

Proof

According to Lemma 1, the following inequation holds for $i\ge r$

$$\begin{aligned} \begin{aligned} \mathcal {P}(\mathbf {Y}_{i+1})-\mathcal {P}(\mathbf {Y}_{i})\ge \eta \left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{2}^{2} \end{aligned} \end{aligned}$$

(44)

which equals to

$$\begin{aligned} \begin{aligned} \left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}\le \frac{1}{\eta }\left[ \mathcal {P}(\mathbf {Y}_{i+1})-\mathcal {P}(\mathbf {Y}_{i}))\right] \end{aligned} \end{aligned}$$

(45)

Given $t>r$, summing the above inequality over $i=r,\ldots ,t-1$ gives

$$\begin{aligned} \begin{aligned} \sum _{i=r}^{t-1}\left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}\le \frac{1}{\eta }\left[ \mathcal {P}(\mathbf {Y}_{t})-\mathcal {P}(\mathbf {Y}_{r})\right] \end{aligned} \end{aligned}$$

(46)

It can be verified that

$$\begin{aligned} \begin{aligned} \min _{i=r,\ldots ,t-1}\left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}&\le \frac{1}{t-r}\sum _{i=r}^{t}\left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}\\&\le \frac{\mathcal {P}(\mathbf {Y}_{t})-\mathcal {P}(\mathbf {Y}_{r})}{(t-r)\eta } \end{aligned} \end{aligned}$$

(47)

indicating that

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\min _{i=r,\ldots ,t-1}\left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}=0 \end{aligned} \end{aligned}$$

(48)

which indicates that $\left\| {\mathbf {Y}_{i+1}-\mathbf {Y}_{i}}\right\| _{F}^{2}\rightarrow 0$ at some iteration t. Therefore, we have

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }[\left\| {\mathbf {Y}_{t}-\mathbf {Y}_{t-1}}\right\| _{F}^{2}]=0 \end{aligned} \end{aligned}$$

(49)

$\square$

Finally, we prove Theorem 3 as follow:

Proof

We first note that problem (13) has a finite number of $n^c$ possible solutions since $\mathbf {Y}$ is a cluster indicator matrix. According to Lemma 3, we know that Algorithm 2 monotonically increases the objective function value of problem (13) in each iteration. Hence, the result follows. $\square$

D Determination of $\eta ^{u}$

Denote $\eta ^{u}=\eta ^{u}_1+\eta ^{u}_2$ and rewrite ${\mathbf {M}}^{l}$ as ${\mathbf {M}}^{l}={\mathbf {M}}^{l}_1+{\mathbf {M}}^{l}_2$. where

$$\begin{aligned} {\mathbf {M}}^{l}_1=2s_{ll}\mathbf {A}+\eta ^{u}_1\mathbf {I}_n \end{aligned}$$

(50)

and

$$\begin{aligned} {\mathbf {M}}^{l}_2=\eta ^{u}_{2}\mathbf {I}_n-s_{ll}^{2}{\mathbf {1}}{\mathbf {1}}^{T} \end{aligned}$$

(51)

It can verified that ${\mathbf {M}}^{l}$ is positive semi-definite if ${\mathbf {M}}^{l}_1$ and ${\mathbf {M}}^{l}_2$ are positive semi-definite.

Suppose the eigendecomposition of $\mathbf {A}$ is $\mathbf {A}=\mathbf {U}_{A}\Sigma _{A}\mathbf {U}^{-1}_{A}$, we have

$$\begin{aligned} {\mathbf {M}}^{l}_1=\mathbf {U}_{A}(2s_{ll}\Sigma _{A}+\lambda _1\mathbf {I}_n)\mathbf {U}^{-1}_{A} \end{aligned}$$

(52)

We know that the diagonal elements in the diagonal matrix $2s_{ll}\Sigma _{A}+\lambda _1\mathbf {I}_n$ are eigenvalues of ${\mathbf {M}}^{l}_1$. To make ${\mathbf {M}}^{l}_1$ positive semi-definite, we only need to make all of its eigenvalues non-negative. Therefore, we can set $\lambda _1$ such that the following inequation holds for $\forall i$

$$\begin{aligned} \eta ^{u}_1\ge -2s_{ll}\sigma _{i}(\Sigma _{A}) \end{aligned}$$

(53)

where $\sigma _{i}(\Sigma _{A})$ is the i-th eigenvalue of $\Sigma _{A}$. The proper $\eta ^{u}_1$ can be set to the maximal value of $-2s_{ll}\sigma _{i}(\Sigma _{A})$. Since $\mathbf {A}$ is normalized and $a_{ii}=0$, we know that $|\sigma (\Sigma _{A})|\le 1$ according to the Gershgorin circle theorem. Therefore, we can set $\eta ^{u}_1=2 \max _{l}s_{ll}$ in order to make ${\mathbf {M}}_1$ positive semi-definite.

On the other hand, ${\mathbf {M}}^{l}_2$ can be rewritten as

$$\begin{aligned} {\mathbf {M}}^{l}_2={\mathbf {V}}\left( \eta ^{u}_{2}\mathbf {I}_n-s_{ll}^{2} \left[ \begin{array}{lll} n &{}\quad \cdots &{}\quad \cdots \\ \cdots &{}\quad \cdots &{}\quad \cdots \\ \cdots &{}\quad \cdots &{}\quad 0\\ \end{array} \right] \right) {\mathbf {V}}^{-1} \end{aligned}$$

(54)

where ${\mathbf {V}}$ consists of the eigenvectors of ${\mathbf {1}}{\mathbf {1}}^{T}$. Since ${\mathbf {M}}^{l}_2$ is positive semi-definite if and only if all of its eigenvalues are non-negative, which leads to $\eta ^{u}_2-ns_{ll}^{2}\ge 0$ and $\eta ^{u}_2-0\ge 0$. Therefore, we can set $\eta ^{u}_2=\max _{l}ns_{ll}^{2}$ to make ${\mathbf {M}}_2$ positive semi-definite.

Finally, we reach the upper bound of $\eta$ as follow

$$\begin{aligned} \eta ^{u}=\max _{l}(2 s_{ll}+ns_{ll}^{2}) \end{aligned}$$

(55)

$\eta ^{u}$ can be updated after updating ${\mathbf {S}}$ in each iteration.