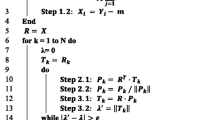Abstract
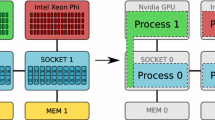
In this paper we consider the l 1-compressive sensing problem. We propose an algorithm specifically designed to take advantage of shared memory, vectorized, parallel and many-core microprocessors such as the Cell processor, new generation Graphics Processing Units (GPUs) and standard vectorized multi-core processors (e.g. quad-core CPUs). Besides its implementation is easy. We also give evidence of the efficiency of our approach and compare the algorithm on the three platforms, thus exhibiting pros and cons for each of them.








Similar content being viewed by others
Notes
More informations can be found on the website: http://www.nvidia.com/object/cuda_home.html.
References
Al-Kiswany, S., Gharaibeh, A., Santos-Neto, E., Yuan, G., & Ripeanu, M. (2008). StoreGPU: Exploiting graphics processing units to accelerate distributed storage systems. In: Proceedings of the 17th international symposium on high performance distributed computing (HPDC) (pp. 165–174).
Andrecut, M. (2009). Fast GPU implementation of sparse signal recovery from random projections. Engineering Letters, 17(3), 151–158.
Bader, D. A., & Agarwal, V. (2007). FFTC: Fastest fourier transform for the IBM cell broadband engine. In: S. Aluru, M. Parashar, R. Badrinath, & V. K. Prasanna (Eds.), HiPC, Lecture of Notes in Computer Science (Vol. 4873, pp. 172–184). Springer.
Bajwa, W. U., Haupt, J. D., Raz, G. M., Wright, S. J., & Nowak, R. D. (2007). Toeplitz-structured compressed sensing matrices. In: Proceedings of the 14th IEEE/SP workshop on Statistical Signal Processing (SSP) (pp. 294–298).
Bernstein, D. J. (2007). The tangent FFT. In: S. Boztas & H. Feng Lu (Eds.), Lecture notes in computer science, applied algebra, algebraic algorithms and error-correcting codes (Vol. 4851, pp. 291–300). Springer.
Bertsekas, D. (1996). Constrained optimization and lagrange multiplier methods. Athena Scientific.
Bioucas-Dias, J., & Figueiredo, M. (2007). A new TwIST: Two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Transactions on Image Processing, 16(12), 2992–3004.
Bredies, K., & Lorenz, D. A. (2008). Iterated hard shrinkage for minimization problems with sparsity constraints. SIAM Journal on Scientific Computing, 30(2), 657–683.
Candès, E., & Romberg, J. (2006). Quantitative robust uncertainty principles and optimally sparse decompositions. Foundations of Computational Mathematics, 6, 227–254.
Candès, E., Romberg, J., & Tao, T. (2006). Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory, 52(2), 489–509.
Candès, E., & Tao, T. (2006). Near optimal signal recovery from random projections: universal encoding strategies?. IEEE Transactions on Information Theory, 52(12), 5406–5426.
Cevher, V., Sankaranarayanan, A., Duarte, M. F., Reddy, D., Baraniuk, R. G., & Chellappa, R. (2008). Compressive sensing for background subtraction. In: Proceedings of the 10th European Conference on Computer Vision (ECCV) (Vol. 5303, pp. 155–168).
Chambolle, A., DeVore, R. A., Lee, N.-Y., & Lucier, B. J. (1998). Nonlinear wavelet image processing: variational problems, compression, and noise removal through wavelet shrinkage. IEEE Transactions on Image Processing, 7, 319–335.
Combettes, P., & Pesquet, J.-C. (2007). Proximal thresholding algorithm for minimization over orthonormal bases. SIAM Journal on Optimization, 18(4), 1351–1376.
Dagum, L., & Menon, R. (1998). OpenMP: An industry standard API for shared-memory programming. IEEE Computational Science and Engineering, 5(1), 46–55.
Daubechies, I., Defrise, M., & Mol, C. D. (2004). An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications in Pure and Applied Mathematics, 57(11), 1413–1457.
DeVore, R. A. (2007). Deterministic constructions of compressed sensing matrices. Journal of Complexity, 4–6(23), 918–925.
Diefendorff, K., Dubey, P., Hochsprung, R., & Scale, H. (2000). Altivec extension to PowerPC accelerates media processing. IEEE Micro, 20(2), 85–95.
Donoho, D., Tsaig, Y., Drori, I., & Starck, J.-L. (2006). Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit. Tech. rep.
Donoho, D. L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289–1306.
Dupe, F.-X., Fadili, J., & Starck, J.-L. (2008). A proximal iteration for deconvolving poisson noisy images using sparse representations. IEEE Transactions on Image Processing, 16(12), 2992–3004.
Hale, W. Y. E. T., & Zhang, Y. (2007). A fixed-point continuation method for l1-regularized minimization with applications to compressed sensing. Tech. rep., Rice University.
Elad, M. (2006). Why simple shrinkage is still relevant for redundant representation? IEEE Transactions on Information Theory, 52, 5559–5569.
Fabritiis, G. D. (2007). Performance of the cell processor for biomolecular simulations. Computer Physics Communications, 176(11–12), 660–664.
Figueiredo, M., & Nowak, R. (2003). An EM algorithm for wavelet-based image restoration. IEEE Transactions on Image Processing, 12(8), 906–916.
Figueiredo, M., Nowak, R., & Wright, S. (2007). Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE Journal of Selected Topics in Signal Processing, 1(3), 586–598.
Frigo, M., & Johnson, S. (1998). FFTW: an adaptive software architecture for the FFT. In: Proceedings of the IEEE international conference on acoustics, speech and signal processing (Vol. 3, pp. 1381–1384).
Gilbert, A. C., Strauss, M. J., Tropp, J. A., & Vershynin, R. (2006). Algorithmic linear dimension reduction in the l 1 norm for sparse vectors. In: Proceedings of the 44th Annual Allerton Conference on Communication, Control and Computing (pp. 1411–1418).
Goldstein, T., & Osher, S. (2008). The split Bregman method for l1 regularized problems. Tech. Rep. CAM 08-29, UCLA.
Griesse, R., & Lorenz, D. A. (2008). A semismooth Newton method for Tikhonov functionals with sparsity constraints. Inverse Problems, 24(3).
Hegde, C., Wakin, M., & Baraniuk, R. (2007). Random projections for manifold learning. In: Neural Information Processing Systems (NIPS).
Hiriart-Urruty, J.-B., & Lemaréchal, C. (1996). Convex analysis and minimization algorithms. Springer, Heidelberg, two volumes—2nd printing.
Kim, S.-J., Koh, K., Lustig, M., Boyd, S., & Gorinevsky, D. (2007). An interior-point method for large-scale l 1-regularized least squares. IEEE Journal of Selected Topics in Signal Processing, 1(4), 606–617.
Kurzak, J., & Dongarra, J. (2007). Implementation of mixed-precision in solving systems of linear equations on the CELL processor. Concurrency and Computation: Practice and Experience, 19(10), 1371–1385.
Lemaréchal, C., & Sagastizábal, C. (1997). Practical aspects of the Moreau-Yosida regularization: theoretical preliminaries. SIAM Journal on Optimization, 7(2), 367–385.
Lieberman, M. D., Sankaranarayanan, J., & Samet, H. (2008). A fast similarity join algorithm using graphics processing units. In: Proceedings of the IEEE international conference on data engineering (ICDE) (pp. 1111–1120).
Lustig, M., Donoho, D., & Pauly, J. M. (2007). Sparse MRI: the application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 58(6), 1182–1195.
Mairal, J., Bach, F., Ponce, J., Sapiro, G., & Zisserman, A. (2008). Discriminative learned dictionaries for local image analysis. In: IEEE Conf. on computer vision and pattern recognition (CVPR) (pp. 23–28).
Moreau, J. (1965). Proximité et dualité dans un espace hilbertien. Bulletin de la S.M.F., 93, 273–299.
Nickolls, J., Buck, I., Garland, M., & Skadron, K. (2008). Scalable parallel programming with CUDA. Queue, 6(2), 40–53.
Nikolova, M. (1999). Markovian reconstruction using a GNC approach. IEEE Transactions on Image Processing, 8(9), 1204–1220.
Nikolova, M., Idier, J., & Mohammad-Djafari, A. (1998). Inversion of large-support ill-posed linear operators using a piecewise Gaussian MRF. IEEE Transactions on Image Processing, 8(4), 571–585.
Nikolova, M., Ng, M. K., Zhang, S. Q., & Ching, W. K. (2008). Efficient reconstruction of piecewise constant images using nonsmooth nonconvex minimization. SIAM Journal on Imaging Sciences, 1(1), 2–25.
Nowak, R., & Figueiredo, M. (2001). Fast wavelet-based image deconvolution using the em algorithm. In: Proceedings of the 35th Asilomar conference on signals, systems, and computers (pp. 371–275).
O’Brien, K., O’Brien, K. M., Sura, Z., Chen, T., & Zhang, T. (2008). Supporting OpenMP on cell. International Journal of Parallel Programming, 36(3), 289–311.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M., Kruger, J., Lefohn, A. E., et al. (2007). A survey of general-purpose computation on graphics hardware. Computer Graphics Forum, 26(1), 80–113.
Pham, D., Asano, S., Bolliger, M., Day, M. N., Hofstee, H. P., Johns, C., et al. (2005). The design and implementation of a first-generation CELL processor. In: Proceedings of the solid-state circuits conference (pp. 184–185).
Seiler, L., Carmean, D., Sprangle, E., Forsyth, T., Abrash, M., Dubey, P., et al. (2008). Larrabee: a many-core x86 architecture for visual computing. In: ACM SIGGRAPH 2008 papers (pp. 1–15). New York, NY, USA: ACM.
Tibshirani, R. (2006). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B, 58, 267–288.
Tropp, J. (2006). Just relax: Convex programming methods for identifying sparse signals. IEEE Transactions on Information Theory, 51(3), 1030–1051.
Tropp, J. A. (2004). Greed is good: algorithmic results for sparse approximation. IEEE Transactions on Information Theory, 50(10), 2231–2242.
Williams, S., Carter, J., Oliker, L., Shalf, J., & Yelick, K. (2008). Lattice Boltzmann simulation optimization on leading multicore platforms. In IEEE international parallel and distributed processing symposium (pp. 1–14).
Williams, S., Shalf, J., Oliker, L., Kamil, S., Husbands, P., & Yelick, K. (2006). The potential of the cell processor for scientific computing. In: Proceedings of the 3rd conference on computing frontiers (CF) (pp. 9–20). New York, NY, USA: ACM.
Wright, J., Yang, A., Ganesh, A., Sastry, S., & Ma, Y. (2009). Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(2), 210–227.
Yin, W., Osher, S., Goldfarb, D., & Darbon, J. (2008). Bregman iterative algorithms for l1-minimization with applications to compressed sensing. SIAM Journal on Imaging Sciences, 1(1), 143–168.
Yosida, K. (1965). Functional analysis. Springer.
Acknowledgements
The research of A. Borghi on this work has been done while being at the mathematics department of UCLA and being supported by the ONR grant N000140710810. The research of J. Darbon and S. Osher was supported by ONR grant N000140710810. The research of T. Chan was supported by DMS-0610079 and ONR N00014-06-1-0345. This works has been supported in part by French National Research Agency (ANR) through COSINUS program project (MIDAS no. ANR-09-COSI-009).
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of Convergence
Appendix: Proof of Convergence
We briefly show the standard elements of the proof of the convergence of the proximal iterations. Recall that the approach is quite standard and some proof can be adapted for [32, 35] for instance.
First, let us note that the series \(\{E_\mu\left(p(u^{(k)})\right)\}\) is clearly non-increasing and bounded by below, and thus converges toward some value referred to as η.
Then, let us recall a standard convex optimality result. Assume that \(g:\mathbb{\bf{R}}^N\rightarrow \mathbb{\bf{R}}\) is convex and differentiable and \(h:\mathbb{\bf{R}}^N \rightarrow \mathbb{\bf{R}}\) is convex, then u ⋆ is a global minimizer of (g + h) if and only if the following holds:
For our case, let us have \(g(\cdot) = \frac{1}{2}\| \cdot - u ^{(k)}\|_M^2\) and h(·) = E μ (·) and recall that \(p_\mu(u ^{(k)})\) is the global minimum of the inf-convolution when it is fed with u (k):
Now, we consider this inequality for the two points \(\hat{u}\) and \(\bar{u}\) with associated proximal points \(p(\hat{u})\) and \(p(\bar{u})\), respectively. Some simple calculus lead to:
and thus we get:
The latter is equivalent to:
Now, let us set \(\bar{u}\) to a global minimizer of R μ , i.e., \(\bar{u} = u^\star\), and \(\hat{u} = u^{(k)}\), in the previous inequality. Note that \(p\left(u^\star\right) = u^\star\), and recall that \(u^{(k+1)} = p\left(u^{(k)}\right)\). The following inequality holds:
With this inequality we can conclude using the following points.
The series \(\| u^{(k)} - u^\star\|_M^2\) is non-increasing and bounded by below (by \(E_\mu(u ^\star))\)) and thus does converge. Thus, we deduce that \(\lim_{k \rightarrow \infty} \left( \| u^{(k+1)} - u^\star \|_M^2 - \| u^{(k)} -\right.\) \( \left.u^\star \|_M^2 \right) = 0\,.\) Using this result and Eq. 7 we get that \(\lim_{k\rightarrow \infty} \| u^{(k+1)} - u^{(k)}\|_M^2 = 0\,.\)
Note that by the convexity of the energy E μ , we have:
Since u (k + 1) is the global minimizer of F μ , we have that:
Recall that, as it has been shown above, \(\lim_{k\rightarrow + \infty} \| u^{(k+1)} - u^{(k)}\|^2 = 0\), and since ||u (k + 1) − u ⋆ ||2 is bounded we have that \(\lim \inf_{k\rightarrow + \infty} \left\langle \partial E_\mu(u ^{(k+1)}),{\kern-4.5pt} \right.\) \(\left.u^{\star} - u^{(k+1)}\right\rangle \geq 0\,.\) Injecting this information into Eq. 8, we obtain that \(\lim_{k \rightarrow + \infty} E_\mu\left(u^{(k)}\right) \leq \eta\), and thus we conclude that \(\lim_{k\rightarrow + \infty} E_\mu(u^{(k)}) = \eta\,.\)
Rights and permissions
About this article
Cite this article
Borghi, A., Darbon, J., Peyronnet, S. et al. A Simple Compressive Sensing Algorithm for Parallel Many-Core Architectures. J Sign Process Syst 71, 1–20 (2013). https://doi.org/10.1007/s11265-012-0671-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11265-012-0671-9