Skip to main content

Advertisement

Springer Nature Link
Log in

A New Variable-Regularized Transform-Domain NLMS Algorithm with Automatic Step-Size Selection for Adaptive System Identification/ Filtering

  • Published:
Journal of Signal Processing Systems Aims and scope Submit manuscript

Abstract

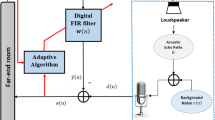
A new variable-regularized (VR) switch-mode noise-constrained (SNC) transform-domain normalized least mean squares (VR-SNC-TDNLMS) algorithm for adaptive system identification and filtering is proposed. It exploits prior knowledge of the additive noise variance and results in a generalized VR-TDNLMS algorithm with a variable step-size (VSS) for improving convergence speed. It also reduces estimation variance, sensitivity to input signal level and eigenvalue spread by means of variable-regularization and decorrelation transformation. To select the variable step-size online, the convergence behavior of the proposed algorithm is analyzed. From the mean convergence analysis, the maximum step-size (MSS) for convergence is first determined. The theoretical results suggest that improved performance can be obtained if the MSS is employed initially while the NC adaptation is adopted near convergence to reduce steady- state misadjustment. Therefore, a switch-mode scheme which employs a MSS mode together with a NC mode is incorporated to further improve its convergence speed. The mean square convergence behavior is also studied by means of a Lyapunov stability-based method to characterize its convergence condition and steady-state misadjustment. Based on the theoretical results, a new automatic threshold selection method for mode switching is developed. General recommendations for choosing other algorithmic parameters are also proposed to facilitate its online and practical usage. The proposed method is expected to find a wide range of applications in areas related to instrumentation and measurement involving low-complexity and recursive linear estimation. In particular, its potential application and effectiveness in system identification problems and several acoustic applications are demonstrated by computer simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7

Similar content being viewed by others

Notes

  1. Though the concept of using two or more step-sizes for adaptation is simple intuitively, it is somewhat difficult to be fully utilized in practice as the switching threshold between the operating modes is difficult to be determined.

  2. The measurement noise may result from quantization errors, modeling errors, etc. and is usually assumed to be white Gaussian distributed. In many practical situations, some prior knowledge on noise variances is also available.

References

  1. Chan, S.C., Chu, Y.J, Tsui, K.M., & Zhang, Z.G. (2011). A new switch- mode noise-constrained transform domain NLMS adaptive filtering algorithm. in Proceedings IEEE International Conference Circuits and System, Rio de Janeiro, Brazil, May 15–18.

  2. Haykin, S. Adaptive filter theory. 4th edition, Prentice Hall, 2001.

  3. Nagumo, J. I., & Noda, A. (1967). A learning method for system identification. IEEE Transaction on Automatic Control, AC-12(3), 282–287.

    Article  Google Scholar 

  4. Liu, S. J., Qi, P. P., Wang, J. S., Zhang, M. H., & Jiang, W. S. (2012). Adaptive calibration of channel mismatches in time-interleaved ADCs based on equivalent signal recombination. IEEE Transactions on Instrumentation and Measurement, 63(2), 277–286.

    Article  Google Scholar 

  5. Saha, M., Ghosh, R., & Goswami, B. (2012). Robustness and sensitivity metrics for tuning the extended Kalman filter. IEEE Transactions on Instrumentation and Measurement, 63(4), 964–971.

    Article  Google Scholar 

  6. Kuo, S. M., & Morgan, D. R. (1996). Active noise control systems – Algorithms and DSP implementations. New York: Wiley.

    Google Scholar 

  7. Zhang, Z. G., Chan, S. C., & Wang, C. (2012). A new regularized adaptive windowed lomb periodogram for time-frequency analysis of nonstationary signals with impulsive components. IEEE Transactions on Instrumentation and Measurement, 61(8), 2283–2304.

    Article  Google Scholar 

  8. Narayan, S., Peterson, A. M., & Narasimha, M. J. (1983). Transform domain LMS algorithm. IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-31, 609–615.

    Article  Google Scholar 

  9. Chan, S.C., & Zhou, Y. (2008). On the convergence analysis of the transform domain normalized LMS and related M-estimate algorithms,” in Proceedings of IEEE APCCAS 2008, Macao, Nov 30-Dec 3.

  10. Beaufays, F. (1995). Transform-domain adaptive filters: an analytical approach. IEEE Transactions on Signal Processing, 43(2), 422–431.

    Article  Google Scholar 

  11. Chan, S.C., Chu, Y.J, & Zhang, Z.G. (2010). A new regularized transform-domain NLMS adaptive filtering algorithm. in Proceeding of APCCAS 2010, Kuala Lumpur, Malaysia, Dec. 6–9.

  12. Wei, Y., Gelfand, S. B., & Krogmeier, J. V. (2001). Noise-constrained least mean squares algorithm. IEEE Transactions on Signal Processing, 49(9), 1961–1970.

    Article  Google Scholar 

  13. Kwong, R. H., & Johnston, E. W. (1992). A variable step size LMS algorithm. IEEE Transactions on Signal Processing, 40(7), 1633–1642.

    Article  MATH  Google Scholar 

  14. Aboulnasr, T., & Mayyas, K. (1997). A robust variable step-size LMS-type algorithm: analysis and simulations. IEEE Transactions on Signal Processing, 45(3), 631–639.

    Article  Google Scholar 

  15. Koike, S. (2002). A class of adaptive step-size control algorithms for adaptive filters. IEEE Transactions on Signal Processing, 50(6), 1315–1326.

    Article  MathSciNet  Google Scholar 

  16. Mathews, V. J., & Xie, Z. (1993). A stochastic gradient adaptive filter with gradient adaptive stepsize. IEEE Transactions on Signal Processing, 41(6), 2075–2087.

    Article  MATH  Google Scholar 

  17. Vega, L. R., Rey, H., Benesty, J., & Tressens, S. (2008). A new robust variable step-size NLMS algorithm. IEEE Transactions on Signal Processing, 56(5), 1878–1893.

    Article  MathSciNet  Google Scholar 

  18. Chan, S.C., Zhang, Z.G., Zhou, Y, & Hu, Y. (2008). A new noise-constrained normalized least mean squares adaptive filtering algorithm in Proceedings of 9 th IEEE Asia Pacific Conference Circuits and System, Macao, China, Dec. 2008.

  19. Chan, S.C., Chu, Y.J., Zhang, Z.G, & Zhou, Y. (2009). On the convergence behavior of the noise-constrained NLMS algorithm in Procedings of IEEE International Conference Circuits and System, Taipei, May 24–27.

  20. Mayyas, K. (2005). A new variable step size control method for the transform domain LMS adaptive algorithm. Journal of Circulation System and Signal Process, 24(6), 703–721.

    Article  MathSciNet  MATH  Google Scholar 

  21. Harris, R., et al. (1986). A variable step size (VSS) algorithm. IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-34, 499–510.

    Google Scholar 

  22. Evans, J. B., Xue, P., & Liu, B. (1993). Analysis and implementation of variable step size adaptive algorithms. IEEE Transactions on Signal Processing, 41(8), 2517–2535.

    Article  MATH  Google Scholar 

  23. Fan, J., & Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association, 96(456), 1348–1360.

    Article  MathSciNet  MATH  Google Scholar 

  24. Chen, Y., Gu, Y., & Hero, A.O. (2009). Sparse LMS for system identification. in Proceedings of ICASSP 2009, pp. 3125–3128, Taipei, Taiwan, April 19–24.

  25. Chan, S. C., Chu, Y. J., & Zhang, Z. G. (2013). A new variable regularized transform domain NLMS adaptive filtering algorithm – acoustic applications and performance analysis. IEEE Transactions on Audio, Speech and Language Processing, 21(4), 868–878.

    Article  Google Scholar 

  26. Gelfand, S. B., Wei, Y., & Krogmeier, J. V. (1999). The stability of variable step-size LMS algorithms. IEEE Transactions on Signal Processing, 47(12), 3277–3288.

    Article  MATH  Google Scholar 

  27. Chan, S. C., Zhang, Z. G., & Chu, Y. J. (2011). A new transform-domain regularized recursive least M-estimate algorithm for robust linear estimation. IEEE Transaction on Circuits System II, 58(2), 120–128.

    Article  Google Scholar 

  28. Zhang, Z.G., Chan, S.C., Zhou, Y., & Hu, Y. (2009). Robust linear estimation using M-estimation and weighted L1 regularization: Model selection and recursive implementation. in Proceedings of IEEE ISCAS 2009, Taipei, May 24–27.

  29. Kamenetsky, M., & Widrow, B. (2004). A variable leaky LMS adaptive algorithm. Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, 1, 125–128.

    Google Scholar 

  30. Widrow, B., McCool, J. M., Larimore, M. G., & Johnson, C. R. (1976). Stationary and nonstationary learning characteritic of the LMS adaptive filter. Proceedings of the IEEE, 64, 1151–1162.

    Article  MathSciNet  Google Scholar 

  31. Feuer, A., & Weinstein, E. (1985). Convergence analysis of LMS filters with uncorrelated Gaussian data. IEEE Transaction on Acoustic Speech and Signal Process, ASSP-33(1), 222–230.

    Article  Google Scholar 

  32. Quatieri, T. (2001). Discrete-time speech signal processing, Prentice Hall.

Download references

Author information

Authors and Affiliations

  1. Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, Hong Kong

    S. C. Chan & Y. J. Chu

Authors
  1. S. C. Chan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Y. J. Chu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. C. Chan.

Additional information

A preliminary version of the SNC-TDNLMS algorithm was presented in IEEE ISCAS’2011 [1]. An improved version using a maximum step-size mode and variable regularization is proposed in the paper. Moreover, a detailed performance analysis using Lyapunov function for step size selection is presented.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chan, S.C., Chu, Y.J. A New Variable-Regularized Transform-Domain NLMS Algorithm with Automatic Step-Size Selection for Adaptive System Identification/ Filtering. J Sign Process Syst 84, 181–196 (2016). https://doi.org/10.1007/s11265-015-1036-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11265-015-1036-y

Keywords