Deep Unfolded Extended Conjugate Gradient Method for Massive MIMO Processing with Application to Reciprocity Calibration

Abstract

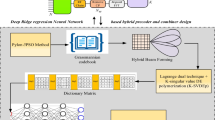
In this paper, we consider deep unfolding the standard iterative conjugate gradient (CG) algorithm to solve a linear system of equations. Instead of being adjusted with known rules, the parameters are learned via backpropagation to yield the optimal results. However, the proposed unfolded CG (UCG) is extended wherein a scalar parameter is substituted by a matrix-parameter to augment the degrees of freedom per layer. Once the training is completed, the UCG has revealed to require far a smaller number of layers than the number of iterations needed using the standard iterative CG. It is also shown to be very robust to noise and outperforms the standard CG in low signal to noise ratio (SNR) region. A key merit of the proposed approach is the fact that no explicit training data is dedicated to the learning phase as the optimization process relies on the residual error which is not explicitly expressed as a function of the desired data. As an example, the proposed UCG is applied to solve the reciprocity calibration problem encountered in massive MIMO (Multiple-Input Multiple-Output) systems.

Appendix 1

The reader must refer to the dependence tree shown in Fig. 1 and to Eqs. (19), (20) and (21) to understand the following derivations. The explicit forms of the gradient of the loss function e with respect to α_k and λ_kare

$$ \overline{\frac{\partial e}{\partial {\alpha}_k}}=2{r}_{n+1}^T\overline{\frac{\partial {r}_{n+1}}{\partial {\alpha}_k}} $$

(A.1)

$$ \overline{\frac{\partial e}{\partial {\lambda}_k}}=2\sum \limits_{z=1}^{2M}{r}_{n+1}^{(z)}\overline{\frac{\partial {r}_{n+1}^{(z)}}{\partial {\lambda}_k}} $$

(A.2)

where $\overline{\frac{\partial \left(\cdot \right)}{\partial \left(\cdot \right)}}$ indicates the total derivative and $\overline{\frac{\partial {r}_{n+1}^{(z)}}{\partial {\lambda}_k}}$ represents the total derivative of the z^th element of r_n + 1 with respect to λ_k where k ∈ [1 : n] for Eq. (A.1) and k ∈ [1 : n − 1] for Eq. (A.2). The formulas for the total derivative of r_n + 1 with respect to α_k and λ_k use

$$ \overline{\frac{\partial {r}_{n+1}}{\partial {\alpha}_n}}=\frac{\partial {r}_{n+1}}{\partial {\alpha}_n} $$

(A.3)

where the total derivative of r_n + 1 with respect to α_n corresponds to the only possible path on Fig. 1 that goes from r_n + 1 to α_n. Before going further, it is important to notice that the allowed paths are those following the same direction as the arrows in Fig. 1. Therefore, we have

$$ \overline{\frac{\partial {r}_{n+1}}{\partial {\alpha}_k}}=\overline{\frac{\partial {r}_{n+1}}{\partial {r}_{k+1}}}\frac{\partial {r}_{k+1}}{\partial {\alpha}_k} $$

(A.4)

where the chain rule is applied between the total derivative of r_n + 1 with respect to r_k + 1, which depends on every possible path on Fig. 1 between r_n + 1 and r_k + 1, and the straight unique path derivative between r_k + 1 and α_k with k ∈ [1 : n − 1]. In a similar way, we derive

$$ \overline{\frac{\partial {r}_{n+1}^{(z)}}{\partial {\lambda}_k}}\left(i,j\right)=\overline{\frac{\partial {r}_{n+1}}{\partial {p}_{k+1}}}\left(i,z\right)\frac{\partial {p}_{k+1}}{\partial {\lambda}_k}\left(i,j\right) $$

(A.5)

where the two indices in parenthesis next to every term represent the row and the column of the resulting matrix with i, j, z ∈ [1 : 2M] and k ∈ [1 : n − 1]. The left-hand side of Eq. (A.5) shows that there is a distinct derivative for each element in the vector r_n + 1 with respect to each (i, j) element in the λ_k matrix. The reason why the form of Eq. (A.5) is slightly different from the one of Eq. (A.4) is due to the fact that λ_k is a matrix instead of being a scalar. We then continue with the total derivative of r_n + 1 with respect to p_n

$$ \overline{\frac{\partial {r}_{n+1}}{\partial {p}_n}}=\frac{\partial {r}_{n+1}}{\partial {p}_n} $$

(A.6)

which is simply the direct path in Fig. 1 between r_n + 1 and p_n. Things get slightly more complicated for the general form of the derivative of r_n + 1 with respect to p_k with k ∈ [2 : n − 1]

$$ \overline{\frac{\partial {r}_{n+1}}{\partial {p}_k}}=\overline{\frac{\partial {r}_{n+1}}{\partial {p}_{k+1}}}\left(\frac{\partial {p}_{k+1}}{\partial {p}_k}+\frac{\partial {p}_{k+1}}{\partial {s}_k}\frac{\partial {s}_k}{\partial {r}_{k+1}}\frac{\partial {r}_{k+1}}{\partial {p}_k}\right)+\overline{\frac{\partial {r}_{n+1}}{\partial {r}_{k+1}}}\frac{\partial {r}_{k+1}}{\partial {p}_k} $$

(A.7)

where the chain rule is first applied between the total derivative of r_n + 1 with respect to p_k + 1, which depends on every possible path on Fig. 1 between these two nodes, and the straight path derivative between p_k + 1 and p_k. In a similar way, the chain rule is applied between the total derivative of r_n + 1 with respect to p_k + 1 and the straight paths derivatives going through p_k + 1, s_k, r_k + 1 and p_k respectively. Finally, the same process is done between the total derivative of r_n + 1 with respect to r_k + 1 and the unique straight path derivative between r_k + 1 and p_k. At that point, the only unknown we are left with is the total derivative of r_n + 1 with respect to any other r. We begin with

$$ \overline{\frac{\partial {r}_{n+1}}{\partial {r}_n}}=\frac{\partial {r}_{n+1}}{\partial {r}_n}+\frac{\partial {r}_{n+1}}{\partial {p}_n}\frac{\partial {p}_n}{\partial {s}_{n-1}}\frac{\partial {s}_{n-1}}{\partial {r}_n} $$

(A.8)

where the first possible path is the direct one between r_n + 1 and r_n and the second possible path is the one that goes through r_n + 1, p_n, s_n − 1 and r_n respectively. We then continue with

$$ {\displaystyle \begin{array}{c}\overline{\frac{\partial {r}_{n+1}}{\partial {r}_{n-1}}}=\overline{\frac{\partial {r}_{n+1}}{\partial {r}_n}}\left(\frac{\partial {r}_n}{\partial {r}_{n-1}}+\frac{\partial {r}_n}{\partial {p}_{n-1}}\frac{\partial {p}_{n-1}}{\partial {s}_{n-2}}\frac{\partial {s}_{n-2}}{\partial {r}_{n-1}}\right)\\ {}\kern2.36em +\frac{\partial {r}_{n+1}}{\partial {p}_n}\frac{\partial {p}_n}{\partial {p}_{n-1}}\frac{\partial {p}_{n-1}}{\partial {s}_{n-2}}\frac{\partial {s}_{n-2}}{\partial {r}_{n-1}}\end{array}} $$

(A.9)

where the three possible paths between r_n + 1 and r_n − 1 are considered. Finally, we have the general case for k ∈ [2 : n − 2]

$$ {\displaystyle \begin{array}{c}\overline{\frac{\partial {r}_{n+1}}{\partial {r}_k}}=\overline{\frac{\partial {r}_{n+1}}{\partial {r}_{k+1}}}\left(\frac{\partial {r}_{k+1}}{\partial {r}_k}+\frac{\partial {r}_{k+1}}{\partial {p}_k}\frac{\partial {p}_k}{\partial {s}_{k-1}}\frac{\partial {s}_{k-1}}{\partial {r}_k}\right)\\ {}\kern2.24em +\frac{\partial {r}_{n+1}}{\partial {p}_n}\left(\prod \limits_{i=n}^{k+1}\frac{\partial {p}_i}{\partial {p}_{i-1}}\right)\frac{\partial {p}_k}{\partial {s}_{k-1}}\frac{\partial {s}_{k-1}}{\partial {r}_k}\\ {}\kern2.24em +\sum \limits_{j=1}^{n-k-1}\left(\overline{\frac{\partial {r}_{n+1}}{\partial {r}_{n-j+1}}}\frac{\partial {r}_{n-j+1}}{\partial {p}_{n-j}}\prod \limits_{z=n-j}^{k+1}\left(\frac{\partial {p}_z}{\partial {p}_{z-1}}\right)\right)\frac{\partial {p}_k}{\partial {s}_{k-1}}\frac{\partial {s}_{k-1}}{\partial {r}_k}\end{array}} $$

(A.10)

where all possible paths going from r_n + 1 to r_kare selected. By differentiating Eqs. (19), (20) and (21), every symbolic derivative can be replaced by its true value

$$ \Big\{{\displaystyle \begin{array}{c}\frac{\partial {r}_{k+1}}{\partial {r}_k}=I,\frac{\partial {r}_{k+1}}{\partial {p}_k}=-{\alpha}_kA\\ {}\frac{\partial {r}_{k+1}}{\partial {\alpha}_k}=-A{p}_k,\frac{\partial {s}_{k-1}}{\partial {r}_k}=A\\ {}\frac{\partial {p}_{k+1}}{\partial {p}_k}={\lambda}_k,\frac{\partial {p}_{k+1}}{\partial {s}_k}=I\\ {}\frac{\partial {p}_{k+1}}{\partial {\lambda}_k}=\left(\begin{array}{ccc}{p}_k^{(1)}& \dots & {p}_k^{(2M)}\\ {}\vdots & \vdots & \vdots \\ {}{p}_k^{(1)}& \cdots & {p}_k^{(2M)}\end{array}\right)\in {\mathbb{R}}^{2M\times 2M}\end{array}} $$

(A.11)

where I is a 2M × 2M identity matrix and $\frac{\partial {\mathbf{p}}_{k+1}}{\partial {\boldsymbol{\uplambda}}_k}$ is a matrix with the i^th column having a constant value corresponding to the i^th element of p_k.

To get better and faster results during the backpropagation process, the adaptation step for α_k and λ_k can be set to different values and a momentum technique is used on λ_k:

$$ {\lambda}_k\left(t+1\right)={\lambda}_k(t)-{\mu}_1\overline{\frac{\partial e}{\partial {\lambda}_k(t)}}+\beta \left({\lambda}_k(t)-{\lambda}_k\left(t-1\right)\right) $$

(A.12)

$$ {\alpha}_k\left(t+1\right)={\alpha}_k(t)-{\mu}_2\overline{\frac{\partial e}{\partial {\alpha}_k(t)}} $$

(A.13)

where μ₁ and μ₂ are the fixed adaptation step, β is the momentum coefficient between 0 and 1 and t represents the current iteration step (epoch) in the backpropagation process.