Skip to main content

Advertisement

Springer Nature Link
Log in

Hyperspectral Image Completion Via Tensor Factorization with a Bi-regularization Term

  • Published:
Journal of Signal Processing Systems Aims and scope Submit manuscript

Abstract

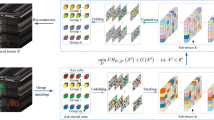
The main purpose of this article is to study a new model of low rank tensor completion. The goal is to predict missing values from a small set of observations. More particular, we present a model of hyperspectral images completion based on a tensor factorization guaranteeing the low rank property and a bi-regularization term promising the preservation of local details in the reconstruction. Such a factorization is used to decompose the tensor as the tensor-matrix mode-3 product of a low-dimensional tensor and a low-dimensional matrix. The bi-regularization term is given by the combination of the piecewise smoothing properties and the coherence constraint between the spectral bands of hyperspectral images. For the minimization process, we consider a Proximal Alternating Minimization (PAM) algorithm to solve the tensor completion model. Several numerical experiments were presented to demonstrate the performance of our proposed method compared to other tensor completion methods in terms of visual and quantitative measurements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6

Similar content being viewed by others

Notes

  1. http://lesun.weebly.com/hyperspectral-data-set.html

  2. http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes#Pavia_Centre_and_University

  3. http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensin_Scenes#Indian_Pines

References

  1. Chang, Y., Yan, L., & Zhong, S. (2017). Hyperspectral image denoising via spectral and spatial low-rank approximation. In 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) (pp. 4193–4196). IEEE.

  2. Yang, J.-H., Zhao, X.-L., Mei, J.-J., Wang, S., Ma, T.-H., & Huang, T.-Z. (2019). Total variation and high-order total variation adaptive model for restoring blurred images with cauchy noise. Computers & Mathematics with Applications, 77(5), 1255–1272.

    Article  MathSciNet  MATH  Google Scholar 

  3. Zhuang, L., & Bioucas-Dias, J. M. (2018). Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 11(3), 730–742.

    Article  Google Scholar 

  4. Li, F., Ng, M. K., & Plemmons, R. J. (2012). Coupled segmentation and denoising/deblurring models for hyperspectral material identification. Numerical Linear Algebra with Applications, 19(1), 153–173.

    Article  MathSciNet  MATH  Google Scholar 

  5. Zhao, X.-L., Wang, F., Huang, T.-Z., Ng, M. K., & Plemmons, R. J. (2013). Deblurring and sparse unmixing for hyperspectral images. IEEE Transactions on Geoscience and Remote Sensing, 51(7), 4045–4058.

    Article  Google Scholar 

  6. Chen, Y., Huang, T.-Z., Zhao, X.-L., & Deng, L.-J. (2018). Hyperspectral image restoration using framelet-regularized low-rank nonnegative matrix factorization. Applied Mathematical Modelling, 63, 128–147.

    Article  MathSciNet  MATH  Google Scholar 

  7. Zhao, Q., Zhang, L., & Cichocki, A. (2015). Bayesian cp factorization of incomplete tensors with automatic rank determination. IEEE transactions on pattern analysis and machine intelligence, 37(9), 1751–1763.

    Article  Google Scholar 

  8. Yokota, T., Lee, N., & Cichocki, A. (2016). Robust multilinear tensor rank estimation using higher order singular value decomposition and information criteria. IEEE Transactions on Signal Processing, 65(5), 1196–1206.

    Article  MathSciNet  MATH  Google Scholar 

  9. Korah, T., & Rasmussen, C. (2007). Spatiotemporal inpainting for recovering texture maps of occluded building facades. IEEE Transactions on Image Processing, 16(9), 2262–2271.

    Article  MathSciNet  Google Scholar 

  10. Ji, T.-Y., Huang, T.-Z., Zhao, X.-L., Ma, T.-H., & Deng, L.-J. (2017). A non-convex tensor rank approximation for tensor completion. Applied Mathematical Modelling, 48, 410–422.

    Article  MathSciNet  MATH  Google Scholar 

  11. Varghees, V. N., Manikandan, M. S., & Gini, R. (2012). Adaptive MRI image denoising using total-variation and local noise estimation. In IEEE-International Conference On Advances In Engineering, Science And Management (ICAESM-2012) (pp. 506–511). IEEE.

  12. Candès, E. J., & Recht, B. (2009). Exact matrix completion via convex optimization. Foundations of Computational mathematics, 9(6), 717–772.

    Article  MathSciNet  MATH  Google Scholar 

  13. Candes, E. J., & Plan, Y. (2010). Matrix completion with noise. Proceedings of the IEEE, 98(6), 925–936.

    Article  Google Scholar 

  14. Liu, J., Musialski, P., Wonka, P., & Ye, J. (2012). Tensor completion for estimating missing values in visual data. IEEE transactions on pattern analysis and machine intelligence, 35(1), 208–220.

    Article  Google Scholar 

  15. Xu, Y., Hao, R., Yin, W., & Su, Z. (2013). Parallel matrix factorization for low-rank tensor completion. Preprint retrieved from http://arxiv.org/abs/1312.1254

  16. Zheng, Y.-B., Huang, T.-Z., Ji, T.-Y., Zhao, X.-L., Jiang, T.-X., & Ma, T.-H. (2019). Low-rank tensor completion via smooth matrix factorization. Applied Mathematical Modelling, 70, 677–695.

    Article  MathSciNet  MATH  Google Scholar 

  17. Mohaoui, S., Hakim, A., & Raghay, S. (2021). Tensor completion via bilevel minimization with fixed-point constraint to estimate missing elements in noisy data. Advances in Computational Mathematics, 47(1), 1–27.

    Article  MathSciNet  MATH  Google Scholar 

  18. He, W., Yao, Q., Li, C., Yokoya, N., & Zhao, Q. (2019). Non-local meets global: An integrated paradigm for hyperspectral denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 6868–6877).

  19. Zheng, Y.-B., Huang, T.-Z., Zhao, X.-L., Chen, Y., & He, W. (2020). Double-factor-regularized low-rank tensor factorization for mixed noise removal in hyperspectral image. IEEE Transactions on Geoscience and Remote Sensing, 58(12), 8450–8464.

    Article  Google Scholar 

  20. Attouch, H., Bolte, J., Redont, P., & Soubeyran, A. (2010). Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the kurdyka-łojasiewicz inequality. Mathematics of operations research, 35(2), 438–457.

    Article  MathSciNet  MATH  Google Scholar 

  21. Attouch, H., Bolte, J., & Svaiter, B. F. (2013). Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized gauss-seidel methods. Mathematical Programming, 137(1), 91–129.

    Article  MathSciNet  MATH  Google Scholar 

  22. Moreau, J. J. (1962). Fonctions convexes duales et points proximaux dans un espace hilbertien. Comptes rendus hebdomadaires des séances de l’Académie des sciences, 255, 2897–2899.

    MathSciNet  MATH  Google Scholar 

  23. Boyd, S., Parikh, N., & Chu, E. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Now Publishers Inc.

  24. Ji, T.-Y., Huang, T.-Z., Zhao, X.-L., Ma, T.-H., & Liu, G. (2016). Tensor completion using total variation and low-rank matrix factorization. Information Sciences, 326, 243–257.

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, X., Ye, Y., & Xu, X. (2017). Low-rank tensor completion with total variation for visual data inpainting. In Proceedings of the AAAI Conference on Artificial Intelligence (vol. 31).

  26. Wang, Z., Bovik, A. C., Sheikh, H. R., & Simoncelli, E. P. (2004). Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing, 13(4), 600–612.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LAMAI, UCAM, FSTG,BP549, Marrakech, Morocco

    Karima EL Qate & Abdelilah Hakim

  2. Université de Toulon, Aix Marseille Université, CNRS, LIS, France, UMR 7020, F-83957 La Garde, Toulon, France

    Karima EL Qate, Eric Moreau & Nadège Thirion-Moreau

  3. MID@S (Math. Computer and D@ta Sciences) Unit, École Centrale Casablanca, R.S. 114, KM 9.5, Route de Nouasseur, Sidi Maârouf, Casablanca, Morocco

    Mohammed El Rhabi

  4. INTERACT Research Unit, UniLaSalle, 60000, Beauvais, France

    Mohammed El Rhabi

Authors
  1. Karima EL Qate
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohammed El Rhabi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Abdelilah Hakim
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Eric Moreau
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Nadège Thirion-Moreau
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Karima EL Qate.

Ethics declarations

Competing Interests

The authors declare that they have no competing interest.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

EL Qate, K., El Rhabi, M., Hakim, A. et al. Hyperspectral Image Completion Via Tensor Factorization with a Bi-regularization Term. J Sign Process Syst 94, 1545–1555 (2022). https://doi.org/10.1007/s11265-022-01817-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11265-022-01817-9

Keywords