Distributed power control algorithms for asynchronous CDMA systems in frequency-selective fading channels

Abstract

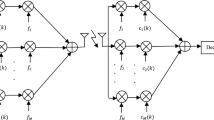
In Code Division Multiple Access (CDMA) radio environments, the maximum number of supportable users per cell is limited by multipath fading, shadowing, multiple access interference and near-far effects which cause fluctuations of the received power at the base station. In this context, power control and signal detection are essential to provide satisfactory Quality of Service (QoS) and to combat the near-far problem in CDMA systems. In this paper, we raised the uplink power control problem for a generalize asynchronous direct-sequence (DS) CDMA system that explicitly incorporate into the analysis: (1) the propagation delays in the network (generally neglected in the literature), (2) the adverse effect of multipath fading for wireless channels, and (3) the asynchronous transmissions in the uplink channels. This framework is used to propose a distributed power control strategy enhanced with linear multiuser receivers. It is shown that through a proper selection of an error function, the nonlinear coupling among active users is transformed into individual linear loops. A Linear-Quadratic-Gaussian (LQG) power control strategy is derived and compared with other approaches from the literature. Simulation results show that the uplink channel variations do not destroy the stability of these power control structures. However, delays in the closed-loop paths can severely affect the stability and performance of the resulting feedback schemes. It is also shown that the use of multiuser detection at the base station can bring significant improvements to the performance of power control.

Appendix

Proof of Proposition 1 by direct substitution of (6) into (19), we get

$$ \begin{aligned} e_i(k)&=p_i(k-n_m)- \gamma^{obj}_i \cdot \sum_{j=-1,j\neq 0}^{1}p_i(k-n_m){\frac{(\varvec{\chi}_i^T\user2{h}_{i,j})^2} {(\varvec{\chi}_i^T\user2{h}_{i,0})^2}}\\ &\quad + \gamma^{obj}_i \cdot \sum_{l=1, l\neq i}^{U}\sum_{j=-1}^{1}p_l(k-n_m){\frac{(\varvec{\chi}_i^T\user2{ h}_{l,j})^2} {(\varvec{\chi}_i^T\user2{h}_{i,0})^2}} + \gamma^{obj}_i\sigma_k^2 \cdot {\frac{\varvec{\chi}_i^T\varvec{\chi}_i} {(\varvec{\chi}_i^T\user2{ h}_{i,0})^2}} \end{aligned} $$

(43)

or equivalently

$$ \begin{aligned} e_i(k)&=\left[1 - \gamma^{obj}_i \cdot \sum_{j=-1,j\neq 0}^{1}{\frac{(\varvec{\chi}_i^T\user2{h}_{i,j})^2}{(\varvec{\chi}_i^T\user2{h}_{i,0})^2}} \right]p_i(k-n_m)\\ &\quad + \gamma^{obj}_i \cdot \sum_{l=1, l\neq i}^{U}\sum_{j=-1}^{1}p_l(k-n_m){\frac{(\varvec{\chi}_i^T\user2{ h}_{l,j})^2} {(\varvec{\chi}_i^T\user2{h}_{i,0})^2}} + \gamma^{obj}_i\sigma_k^2 \cdot {\frac{\varvec{\chi}_i^T\varvec{\chi}_i} {(\varvec{\chi}_i^T\user2{ h}_{i,0})^2}}. \end{aligned} $$

(44)

If we define

$$ \kappa_i \, \triangleq \, 1 - \gamma_i^{obj} \sum_{j=-1}^{1} {\frac{(\varvec{\chi}_i^T\user2{h}_{i,j})^2} {(\varvec{\chi}_i^T\user2{ h}_{i,0})^2}}. $$

(45)

and

$$ \hat{p}_i(k) \, \triangleq \, {\frac{\gamma_i^{obj}}{\kappa_i}} \left[ \sum_{l=1, l\neq i}^U \sum_{j=-1}^{1}p_l(k){\frac{(\varvec{\chi}_i^T\user2{h}_{l,j})^2} {(\varvec{\chi}_i^T\user2{h}_{i,0})^2}}+ \sigma_k^2{\frac{\varvec{\chi}_i^T\varvec{\chi}_i} {(\varvec{\chi}_i^T\user2{h}_{i,0})^2}} \right], $$

(46)

then (19) is obtained. Hence the tracking error e _i [k] in (19) is defined in a nonlinear way as a percentage error weighted by the power level. In fact, if e _i [k] → 0 then $\gamma_i[k] \rightarrow \gamma_i^{obj},$ since p _i [k] ≠ 0. Also, the error is always well-defined, since γ _i  ≠ 0 for an active user. Finally, without loss of generality, it is assumed that $|h_i[k]|^2 \neq 0\;\forall k$ and any active user. $\square$

Proof of Proposition 2 the Dead-Beat control law can be derived by observing the closed-loop relation between the output and reference:

$$ [(1-z^{-1})den_i(z)-z^{-n_{RT}}num_i(z)]P_i(z)=-z^{-n_{RT}}num_i(z) \hat{P}_i(z) $$

(47)

where $P_i(z)={\mathcal{Z}}\{p_i(k)\}$ and $\hat{P}_i(z)={\mathcal{Z}}\{\hat{p}_i(k)\}$ denote the z -transforms of the power signal and its reference. Note that for Dead-Beat response, it is needed $P_i(z)=z^{-n_{RT}}\hat{P}_i(z)$. Considering num _i (z) = b₀ and $den_i(z)=a_0+a_1z^{-1}+a_2z^{-2}+\cdots+a_{n_p+n_m}z^{-(n_p+n_m)},$ then it is concluded that:

$$ a_{n_p+n_m}=a_{n_p+n_m-1}=\cdots=a_1=a_0=-b_0. $$

Consequently, the controller $K^{DB}_i(z)$ in (28) is deduced. $\square$

Proof of Proposition 3 by a direct substitution of (29) into (30), the cost function J can be written as

$$ J \,\triangleq \, \sum_{k=0}^\infty \left \{ {\frac{q}{2}} \, a_i^2(k-1) +q \, a_i(k-1) u_i(k-n_{RT})+ {\frac{q+r}{2}}\, u_i^2(k-n_{RT}) \right\}. $$

(48)

The local stationary conditions for optimality are

$$ \begin{aligned} {\frac{\partial J}{\partial u_i(k-n_{RT})}}&=q a_i(k-1)+(q+r)u_i(k-n_{RT}) = 0\\ {\frac{\partial^2 J}{\partial u_i^2(k-n_{RT})}}&= (q+r)>0. \end{aligned} $$

(49)

Finally, from (49) and by arranging the time indices, the suboptimal control law in (31) is deduced. Next, the closed-loop stability is evaluated. The suboptimal control law $\hat{K}_{SLQ}$ and open-loop plant G can be expressed in z-domain using a transfer function notation

$$ \hat{K}_{SLQ}=-{\frac{q}{q+r}}z^{n_{RT}-1} \quad \& \quad G(z)={\frac{z^{-n_{RT}}}{1-z^{-1}}}. $$

(50)

The closed-loop characteristic equation $1-\hat{K}_{SLQ}G=0$ is given by

$$ 1 - {\frac{r}{q+r}} z^{-1}=0. $$

(51)

Therefore, the closed-loop pole is $0 < {\frac{r}{q+r}}<1,\;\forall q,r>0$. As a result, the feedback system is stable. $\square$

Proof of Proposition 4 the prediction error can be written using a vector notation:

$$ E \,\triangleq \, a_i(k+n_{RT}-1)- \hat{a}_i(k+n_{RT}-1)=({\bf 1}^T-\Uptheta^T){\bf Y}-\Uptheta^T {\bf W}, $$

(52)

where vectors ${\bf 1},{\bf Y},{\bf W}\in {\mathbb{R}}^{n_{RT}},$ and they are represented by

$$ {\bf 1} \, \triangleq \, [1 \ldots 1]^T $$

$$ {\bf Y} \, \triangleq \, \left[ \begin{array}{l} a_i(k)\\ u_i(k-1)\\ \vdots\\ u_i(k-n_{RT}+1) \end{array} \right],\quad\quad {\bf W} \, \triangleq \, \left[ \begin{array}{l} s_i(k)\\ g_i(k-1)\\ \vdots\\ g_i(k-n_{RT}+1) \end{array} \right]. $$

(53)

As a result, the prediction error can be written as

$$ E= {\mathcal{E}} \left \{ \left[{\bf Y}^T({\bf 1}-\Uptheta)-{\bf W}^T \Uptheta \right] \left[ ({\bf 1}^T-\Uptheta^T){\bf Y}-\Uptheta^T {\bf W} \right]\right\}. $$

(54)

This cost function E can be further simplified by applying the statistical properties ${\mathcal{E}} \{ a_i(k) u_i(k-d) \}=0\;\forall k,d$ and ${\mathcal{E}}\{a_i^2(k)\}=\sigma_a^2 {\mathcal{E}} \{ u_i^2(k) \} = \sigma_u^2\;\forall k$ to obtain

$$ E= {\bf 1}^T {\bf P} {\bf 1}+ \Uptheta^T {\bf P} \Uptheta+ \Uptheta^T {\bf Q} \Uptheta $$

(55)

where

$$ \begin{aligned} {\bf P} &= {\mathcal{E}}\{ {\bf Y}{\bf Y}^T \}= \left[ \begin{array}{llll} \chi_a^2 & & &\\ & \chi_u^2 & &\\ & & \ddots &\\ & & & \chi_u^2 \end{array} \right]\\ {\bf Q} &= {\mathcal{E}}\{ {\bf W}{\bf W}^T \}= \left[ \begin{array}{llll} \sigma_s^2 & & &\\ & \sigma_g^2 & &\\ & & \ddots &\\ & & & \sigma_g^2 \end{array} \right]. \end{aligned} $$

Finally, the optimal stationary conditions are derived

$$ {\frac{\partial E}{\partial \Uptheta}} = {\bf P} \Uptheta - {\bf P}\, {\bf 1}+{\bf Q} \Uptheta = {\bf 0} $$

(56)

$$ {\frac{\partial^2 E}{\partial \Uptheta^2}} = {\bf P}+{\bf Q} >0. $$

(57)

Therefore, the optimal solution is given by

$$ \hat{\Uptheta}=({\bf P}+{\bf Q})^{-1}{\bf P} \, {\bf 1} $$

(58)

which is equivalent to (36). $\square$

Proof of Proposition 5 the control law in (37) is readily constructed by using the results from Proposition 3 in (37), and the optimal parameters in the estimation problem of Proposition 4 in (36). $\square$