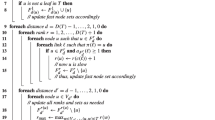The fundamental limits of broadcasting in dense wireless mobile networks

Abstract

In this paper, we investigate the fundamental properties of broadcasting in mobile wireless networks. In particular, we characterize broadcast capacity and latency of a mobile network, subject to the condition that the stationary node spatial distribution generated by the mobility model is uniform. We first study the intrinsic properties of broadcasting, and present the RippleCast broadcasting scheme that simultaneously achieves asymptotically optimal broadcast capacity and latency, subject to a weak upper bound on maximum node velocity and under the assumption of static broadcast source. We then extend RippleCast with the novel notion of center-casting, and prove that asymptotically optimal broadcast capacity and latency can be achieved also when the broadcast source is mobile. This study intendedly ignores the burden related to the selection of broadcast relay nodes within the mobile network, and shows that optimal broadcasting in mobile networks is, in principle, possible. We then investigate the broadcasting problem when the relay selection burden is taken into account, and present a combined distributed leader election and broadcasting scheme achieving a broadcast capacity and latency which is within a $\Uptheta((\log n)^{1+\frac{2}{\alpha}})$ factor from optimal, where n is the number of mobile nodes and α > 2 is the path loss exponent. However, this result holds only under the assumption that the upper bound on node velocity converges to zero (although with a very slow, poly-logarithmic rate) as n grows to infinity.

Appendix

Proof of Lemma 2.

Let us call the cells at cell distance i from the cell containing the source node the i-th ripple. We start showing that: a) for each cell A in the i-th ripple, the leader node of cell A transmits during round t + i the packet generated by the source node at round t. The proof is by induction on i. Property a) trivially holds when i = 0. Assume now property a) holds for each j < i. In order for a) to hold also for i, we need to show that, for any cell A in the i-th ripple, the node selected as leader for A during round t + i, which is going to transmit during round t + i, has received the packet generated by the source at round t before its transmission opportunity during round t + i. Given that a) is assumed to hold for j < i, we have that the leader node of cell B, where B is any of the cells in the (i − 1)-th ripple adjacent to A (note that at least one such cell always exists), has transmitted during round t + i − 1 the packet generated by source node at round t. Given the rules for selecting leader nodes, we have that the leader node at round t + i − 1 for cell B is selected amongst the nodes located in the central mini-cell of B at the beginning of round t + i − 1. By Proposition 1, we have that at least one such node exists, w.h.p. Furthermore, the upper bound $\bar{v}$ on node velocity guarantees that a node travels at most $\bar{v} \bar{k}^2 \tau=\frac{l}{3}$ in the time elapsing between the beginning of round t + i − 1 and the beginning of round t + i. Since the leader node of cell B was within the central mini-cell of cell B at the beginning at round t + i − 1 and given the above observation about the distance traveled by nodes, we have that the leader node of cell B is still within cell B when it is scheduled for transmission during round t + i − 1. Hence, by Proposition 3, we have that the packet transmitted by the leader node of cell B during round t + i − 1, which by induction is the packet generated by the source node at round t, is correctly received by all nodes within cell A at the time of transmission. In particular, the leader node w for cell A at round t + i is within the central mini-cell of A at the beginning of round t + i, which given the above observation about maximum traveled distance, ensures that w was within cell A also during the entire round t + i − 1. Thus, node w can correctly receive the packet sent by the leader node of cell B during round t + i − 1, and can forward it in the network when scheduled for transmission at round t + i, which implies property a).

Let us now define the set of covered cells Cov(p) for a certain packet p as the set of cells such that their respective leader nodes have already transmitted packet p. By property a), and assuming packet p is generated by the source at round t, we have that Cov(p) at round t + i is the union of all the cells in ripples $0,\dots,i$. Given the assumption on the size L(n) of the deployment region, we have that Cov(p) contains all the cells in the deployment region at round $t+\frac{L(n)}{2 l}=t+O(\sqrt{\frac{n}{\log n}})$. Let us now consider an arbitrary mobile node u, and assume by contradiction that node u has not received packet p by the end of round $t+\frac{L(n)}{2 l}$. Since Cov(p) contains all the cells in the deployment region by then, and considering that each of the ripples propagating packet p is a “closed curve”⁸, the only possible way for node u to avoid receiving p is to cut through the ripple propagation front during round j, for some $0<j<\frac{L(n)}{2 l}$. However, for this to be possible, node u should travel distance at least 2l between two successive rounds (see Fig. 5), which is possible only if node velocity is at least $v^{\prime}=\frac{2 l}{2 \bar{k}^2 \tau}>\bar{v}$. Thus, the assumption about maximum node velocity is contradicted, and the Lemma is proved. $\square$

Fig. 5

Assume the source s is somewhere south of the diagrams, and the propagation front of packet p moves northward. Stars represents cell leaders active in a certain round, and the checkered region is the region covered by them. The white area has not yet been covered by packet p, while the gray area represents cells in Cov(p) during a certain round. On the left, a circle represents a node lying in the white area which has not yet received p at a certain round t + j − 1. To avoid reception of packet p, the node must cut the propagation front and reach the gray area during round t + j (right), where p is no longer transmitted. Thus, the node should travel distance at least 2l between the two consecutive rounds

Proof of Lemma 3.

Let us consider now the interference experienced by u under the condition that in each cell with the same color there are at most m nodes. Assume w.l.o.g. that cell(u) has coordinates (0,0). Given the coloring scheme, interferers lie in the cells with bottom left corner at $(x\cdot k\cdot l,y\cdot k\cdot l)$ with $x,y\in\mathbf{Z}$ and (x, y) ≠ (0, 0) (shaded cells in Fig. 2).

The distance d(x, y) between u and an interferer located in cell $(x\cdot k\cdot l,y\cdot k\cdot l),$ with x, y ≠ 0, can be lower bounded as follows:

$$ d(x,y)\ge\sqrt{(|x|kl-l)^2+(|y|kl-l)^2}, $$

(3)

where the term −l depends on the actual positions of u and I inside their respective cells.

Since $a^{2}+b^{2}\ge \left(\max\{a,b\}\right)^{2},$ from (3) we obtain the following lower bound on d(x, y):

$$ \begin{aligned} d(x,y)&\ge\max\{|x|,|y|\}kl-l=l(k\max\{|x|,|y|\}-1)\ge \\ &\ge (k-1)l\max\{|x|,|y|\}. \end{aligned} $$

Note that the last bound is always strictly positive, since we are assuming k ≥ 2 and |x|, |y| are not both 0.

The interference received by u thus satisfies

$$ \begin{aligned} P_I &<m\sum\frac{P}{((k-1)l\max\{|x|,|y|\})^{\alpha}}=\\ &=m\frac{P}{(k-1)^\alpha l^\alpha}\sum\frac{1}{\max\{|x|,|y|\}^\alpha}, \end{aligned} $$

where the sum is extended over all the pairs (x, y) ≠ (0, 0), with $x,y\in \mathbf{Z}$.

Counting twice the contributions along x = 0,  y = 0, and |x| = |y|, we have

$$ \sum\limits_{(x,y)\neq(0,0)}\frac{1}{\max\{|x|,|y|\}^\alpha}< 8\sum\limits_{x=1}^\infty\sum\limits_{y=0}^x\frac{1}{x^\alpha} $$

due to the eightfold symmetry of the summation shown in Fig. 7. Collecting the values for which max(x, y) = x we obtain

$$ 8 \sum\limits_{x=1}^\infty\sum\limits_{y=0}^x\frac{1}{x^\alpha} =8\sum\limits_{x=1}^{\infty}\frac{x+1}{x^\alpha}< 16\sum\limits_{x=1}^\infty\frac{1}{x^{\alpha-1}}=16\zeta(\alpha-1), $$

where $\zeta(\cdot)$ is the Riemann’s zeta function and summarizing we obtain formula (1). $\square$

Fig. 6

The leader election algorithm

Fig. 7

Eightfold symmetry in the derivation of the upper bound to the total interference

Fig. 8

The broadcast scheme with leader election

Fig. 9

Broadcasting with mobile source

Fig. 10

The CenterCast phase of the broadcasting scheme with mobile source

Proof of Lemma 9.

Let P _s denote a minimum-hop cell path connecting cell C(s, i) with C _c . In other words, P _s is a minimum-length sequence of cells $C(s,i)=C_0,\dots,C_j = C_c$ such that, for each $q=0,\dots,j-1,$ cells C _q and C _q+1 are adjacent. We will prove that the packet generated by s at round i is propagated through P _s till it reaches C _c , with the packet progressing one cell at each round. The proof is by induction on the cell distance q from C(s, i). More specifically, we want to prove the following property: a) packet p _i is correctly received by node L(C _q+1,i + q) during round i + q, for any 0 ≤ q ≤ j − 1. Property a) implies the lemma by observing that d(C(s, i), C _c ) = d(s, i) implies existence of a cell path of length d(s, i) connecting cells C(s, i) and C _c .

To prove the base case q = 0, we observe that Lemma 8 ensures that p _i is correctly received by all nodes that are located in cells adjacent to C(s, i)—including cell C ₁—at time t _i  + 2k ²τ. On the other hand, Lemma 7 ensures that node L(C ₁,i) remains within cell C ₁ during the whole duration of rounds i and i + 1. Thus, node L(C ₁,i) is guaranteed to be in cell C ₁ at time t _i  + 2k ²τ, and to correctly receive p _i .

Assume now that property a) holds for any $q^{\prime}<q$. By induction hypothesis, node L(C _q ,i + q − 1) has correctly received p _i at the end of round i + q − 1. We have to prove that p _i will be transmitted by node L(C _q ,i + q − 1) during the next broadcast round i + q. We first observe that, in order for a packet to be transmitted by a non-source node, the packet had to be stored in the transmit buffer upon reception. This happens if and only if the following three conditions are fulfilled: (1) the node is the leader of its cell for the current round; (2) the cellID in the packet equals the cell to which the node belongs; and (3) packet ID is larger than that of the last received packet. It is easy to see that condition (1) is fulfilled at node L(C _q ,i + q − 1). Condition (2) is fulfilled under the assumption, which holds without loss of generality, that the next cell selected by node L(C _q−1,i + q − 2) when transmitting p _i was set to C _q . As for condition (3), we have to prove that packet ordering is preserved when forwarding packets generated by the source towards cell C _c . More specifically, we have to prove that packets p _j with j > i cannot be received by L(C _q ,i + q − 1) before packet p _i . Note that there are two possible ways in which a packet p _j with j > i can be propagated “faster” than packet p _i :—(i) packet p _j is a new packet generated by s, and s has moved along P _s in the direction of C _c ; and—(ii) packet p _j is a packet relayed by a leader node on its route to cell C _c . As for case i), we observe that, by Lemma 6, node s can only move to adjacent cells during a broadcast round, hence its speed cannot exceed the speed of packet p _i propagation towards C _c . Yet, it is possible that, say, node s is located in cell C ₁ at round i + 1, possibly leading to impaired packet ordering in case packet p _i+1 is transmitted by s before packet p _i is forwarded to C ₂ by node L(C ₁,i). However, the transmission slot reserved for source transmission is located after the 2k ² slots allocated for forwarding pending packets to the center cell C _c , hence packet ordering is preserved in case (i). As for case (ii), we observe that it is possible for a leader node to have two packets in the transmit buffer during a certain round (due to, e.g., mobility of the source in the direction of the center cell as explained above). However, in case multiple packets are present in the transmit buffer, older packets are prioritized over newer ones, thus preserving packet ordering also in this case. We have then proved that packet p _i is stored in the buffer of node L(C _q ,i + q − 1) during round i + q − 1. We now have to prove that node L(C _q ,i + q − 1) will transmit this packet during round i + q, and that node L(C _q+1,i + q) correctly receives the packet. As for the first part, observe that nodes in cell C _q have two transmission opportunities during round i + q; since node L(C _q ,i + q − 1) has at most two packets in its transmit buffer (packet p _i , and possibly packet p _j with j = i − 1 or j = i + 1), two transmission opportunities are sufficient for node L(C _q ,i + q − 1) to transmit all packets in the buffer, including packet p _i . To see why at most two packets can be stored in a node’s transmit buffer, it is sufficient to observe that multiple packets are sent by a cell only when the source is traveling, say, from cell C _k to cell C _k+1 in a round j, in which case two packets will be transmitted by cell C _k+1 during round j + 1 (the packet p _j sent by the source at round j, and the new packet p _j+1 generated by the source at round j + 1). If the source would be allowed to move to cell C _k+2 during round j + 2, we would have cell C _k+2 transmitting 3 packets at round j + 2 (packets p _j ,  p _j+1, and the new packet p _j+2 generated by the source at round j + 2). However, Lemma 6 implies that the source cannot move to cell C _k+2 during round j + 2, since it can cross at most one cell during the duration of two broadcast rounds. This implies that every cell transmits at most two packets during any center-cast phase of the broadcast round, which in turns implies that at most two packets can be stored in a node’s transmit buffer.

We are now left to show that node L(C _q+1,i + q) correctly receives packet p _i . By induction hypothesis, by the fact that leader nodes are unique in a cell, and by Lemma 7, we have that the only node in cell C _q that has non-empty transmit buffer during round i + q is L(C _q , i + q − 1), implying that there is no conflicting transmission from other nodes in C _q during node L(C _q ,i + q − 1) transmission(s). In order to prove that node L(C _q+1,i + q) correctly receives p _i , it is sufficient to observe that, by Lemma 7, node L(C _q ,i + q − 1) is still within cell C _q during round i + q, which implies that packets sent by this node during round i + q are correctly received by all nodes in adjacent cells, including node L(C _q+1,i + q). $\square$