Multi-Spreader Routing for sparsely populated mobile ad hoc networks

Abstract

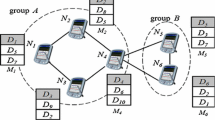
We propose Multi-Spreader Routing, a store-carry-forward routing scheme for sparsely populated mobile ad hoc networks. Multi-Spreader Routing includes Epidemic Routing and Two-Hop Forwarding as special cases, and it can manage trade-off between message delivery delay and resource consumption effectively. We analyze various performance measures of Multi-Spreader Routing with a recovery scheme called VACCINE, and we evaluate its performance. Further, through simulation experiments with real mobility trace data, we demonstrate that Multi-Spreader Routing shows stable performance in various network environments.

Appendices

Appendix 1: Transition rates from state (x, k, 0)

This appendix considers meetings of two nodes in state (${\user2{x}},k,0$).

• 1. A spreader with counter value c _j ($j=1,2,\ldots,n(P)-1$) encounters a vacant node: The vacant node becomes a spreader with counter value ⌊c _j /2⌋. At the same time, the counter value of the spreader is updated to be $\lceil c_j/2 \rceil.$ Therefore the state transition from state (${\user2{x}},k,0$) to state (${\user2{x}}_j^{\prime},k+1,0$) happens, where ${\user2{x}}_j^{\prime}$ is given in (3). Because there are x _j spreaders with counter value c _j and N − k vacant nodes in state (${\user2{x}},k,0$), the transition rate from state (${\user2{x}},k,0$) to state (${\user2{x}}_j^{\prime},k+1,0$) is given by (N − k) x _j λ.

• 2. A spreader with counter value c = 1 encounters a vacant node: The vacant node becomes a relay node. Therefore the state transition from state (${\user2{x}},k,0$) to state (${\user2{x}},k+1,0$) happens and its transition rate is given by (N − k) x _n(P) λ.

• 3. A spreader with counter value c _j ($j=1,2,\ldots,n(P)-1$) encounters a relay node: As stated in Sect. 3.1, the relay node becomes a spreader with counter value ⌊c _j /2⌋. At the same time, the counter value of the spreader is updated to be $\lceil c_j/2\rceil.$ Thus the state transition from state (${\user2{x}},k,0$) to state (${\user2{x}}_j^{\prime},k,0$) happens, where ${\user2{x}}_j^{\prime}$ is given in (3). There are $N_R^{[{\user2{x}},k]}$ relay nodes in state (${\user2{x}},k,0$), where $N_R^{[{\user2{x}},k]}$ is given in (2). Thus the transition rate from state (${\user2{x}},k,0$) to state (${\user2{x}}_j^{\prime},k,0$) is given by $N_R^{[{\user2{x}},k]} x_j \lambda.$

• 4. A spreader encounters the destination node: As soon as the spreader forwards the message to the destination node, both nodes generate the corresponding anti-packets. Therefore, when the counter value of the message that the spreader carries is equal to c _j ($j=1,2,\ldots,n(P)$), the state transition from state (${\user2{x}},k,0$) to state (${\user2{x}} - {\user2{e}}_j,k-1,2$) happens. Because there is only one destination node, the transition rate from state (${\user2{x}},k,0$) to state (${\user2{x}} - {\user2{e}}_j,k-1,2$) is given by x _j λ.

• 5. A relay node encounters the destination node: As soon as the relay node forwards the message copy to the destination node, both nodes generate the corresponding anti-packets. Therefore the state transition from state (${\user2{x}},k,0$) to state (${\user2{x}},k-1,2$) happens, whose transition rate is given by $N_R^{[{\user2{x}},k]} \lambda.$

• 6. Other cases: The numbers of spreaders and message copies remain the same, and therefore the state transition does not occur.

Appendix 2: Transition rates from state (x, k, m)

This appendix considers meetings of two nodes in state $({\user2{x}},k,m)$ (m ≥ 2).

• 1. A spreader with counter value c _j ($j=1,2,\cdots,n(P)-1$) encounters a vacant node: The vacant node becomes a spreader with counter value ⌊c _j /2⌋. At the same time, the counter value of the spreader is updated to be $\lceil c_j/2 \rceil.$ Therefore the state transition from state (${\user2{x}},k,m$) to state (${\user2{x}}_j^{\prime},k+1,m$) happens, where ${\user2{x}}_j^{\prime}$ is given in (3), and its transition rate is given by (N + 1 − k − m) x _j λ because there are x _j spreaders with counter value c _j and N + 1 − k − m vacant nodes in state (${\user2{x}},k,m$).

• 2. A spreader with counter value c _n(P) (=1) encounters a vacant node: The vacant node becomes a relay node. Therefore the state transition from state (${\user2{x}},k,m$) to state (${\user2{x}},k+1,m$) happens, whose transition rate is given by (N + 1 − k − m) x _n(P) λ.

• 3. A spreader with counter value c _j ($j=1,2,\cdots,n(P)-1$) encounters a relay node: The relay node becomes a spreader with counter value ⌊c _j /2⌋. At the same time, the counter value of the spreader is updated to be $\lceil c_j/2 \rceil.$ Therefore the state transition from state $({\user2{x}},k,m)$ to state $({\user2{x}}_j^{\prime},k,m)$ happens. Because the number of relay nodes in state $({\user2{x}},k,m)$ is given by $N_R^{[{\user2{x}},k]}$ in (2), the transition rate is given by $N_R^{[{\user2{x}},k]} x_j \lambda.$

• 4 A spreader encounters a node with an anti-packet: The spreader receives an anti-packet and deletes the message. Therefore, when the spreader has the message with counter value c _j ($j=1,2,\cdots,n(P)$), the state transition from state (${\user2{x}},k,m$) to state (${\user2{x}} - {\user2{e}}_j,k-1,m+1$) happens, and its transition rate is given by m x _j λ because there are m nodes with anti-packets.

• 5. A relay node encounters a node with an anti-packet: The relay node receives an anti-packet and deletes the message copy. Thus the state transition from state (${\user2{x}},k,m$) to state (${\user2{x}},k-1,m+1$) happens and its transition rate is given by $m N_R^{[{\user2{x}},k]} \lambda.$

• 6 A node with an anti-packet encounters a vacant node: The vacant node receives an anti-packet. Therefore the state transitions from state (${\user2{x}},k,m$) to state (${\user2{x}},k,m+1$) happens, and its transition rate is given by m (N + 1 − k − m)λ.

• 7 Other cases: The numbers of spreaders, message copies, and anti-packets remain the same, and therefore the state transition does not occur.

Appendix 3: Mean length of the lifetime of a message

We define $T_E({\user2{x}},k,m)$ ($m=0,2,3,\ldots,N+1,$ ${({\user2{x}},k,m) \in {\mathcal{S}}_P(m)}$) as

$$T_E({\user2{x}},k,m) = \hbox{E}[T_E \mid {\user2{Z}}(0)= ({\user2{x}},k,m)],$$

where T _E is defined in (7). By definition, $\hbox{E}[T_E] = T_E({\user2{e}}_1,1,0).$ It follows from Table 2 that $T_E({\user2{x}},k,0)$ ($N_S^{[{\user2{x}}]} \le k \le N$) satisfies

$$\begin{aligned} T_E({\user2{x}},k,0)&= \frac{1} {\lambda_1({\user2{x}},k,0)} + \sum^{n(P)-1}_{j=1} \frac{ x_j N_R^{[{\user2{x}},k]} \lambda} { \lambda_1({\user2{x}},k,0)} T_E({\user2{x}}_j^{\prime},k,0) \\ & \quad + \sum^{n(P)-1}_{j=1} { \frac{( N - k ) x_j \lambda} {\lambda_1({\user2{x}},k,0)}} T_E({\user2{x}}_j^{\prime},k+1,0) \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{ x_j \lambda} { \lambda_1({\user2{x}},k,0)} T_E({\user2{x}} - {\user2{e}}_j, k - 1, 2) \\ & \quad + {\frac{(N-k) x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} T_E({\user2{x}},k+1,0) \\ & \quad + {\frac{x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} T_E({\user2{x}} - {\user2{e}}_{n(P)}, k - 1, 2) \\ & \quad + \frac{N_R^{[{\user2{x}},k]} \lambda}{\lambda_1 ({\user2{x}},k,0)} T_E({\user2{x}}, k-1, 2),\\ \end{aligned} $$

(9)

where $T_E({\user2{x}},N+1,0) = T_E({\user2{x}},0,0) = T_E({\bf 0},k,0) = 0$.

Also, it follows from Table 3 that for m ≥ 2, the sum $\lambda_2({\user2{x}},k,m)$ (${({\user2{x}},k,m) \in {\mathcal{S}}_P(m)}$) of transition rates from state $({\user2{x}},k,m)$ is given by

$$\begin{aligned} \lambda_2({{\user2{x}},k,m}) &= \sum^{n(P)-1}_{j=1} ( N_R^{[{\user2{x}},k]}+ N - k + 1) x_j \lambda \\ &\quad + ( N - k + 1) x_{n(P)} \lambda \\ & \quad + m N_R^{[{\user2{x}},k]} \lambda + m ( N + 1 - k - m ) \lambda. \\ \end{aligned}$$

Therefore $T_E({\user2{x}},k,m)$ ($N_S^{[{\user2{x}}]} \le k \le N - 1, 2 \le m \le N, k+m \le N+1$) satisfies

$$\begin{aligned} &{T_E({\user2{x}},k,m)} \; \\ &=\frac{1}{\lambda_2({\user2{x}},k,m)} + \sum^{n(P)-1}_{j=1} \frac{N_R^{[{\user2{x}},k]} x_j \lambda}{\lambda_2({\user2{x}},k,m)} T_E({\user2{x}}_j^{\prime}, k,m) \\ & \quad+ \sum^{n(P)-1}_{j=1} \frac{( N + 1 - k - m) x_j \lambda}{\lambda_2({\user2{x}},k,m)} T_E({\user2{x}}_j^{\prime},k+1,m) \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{m x_j \lambda}{\lambda_2({\user2{x}},k,m)} T_E({\user2{x}}-{\user2{e}}_j, k-1, m+1) \\ & \quad + \frac{(N+1-k-m) x_{n(P)} \lambda}{\lambda_2({\user2{x}},k,m)} T_E({\user2{x}}, k+1, m) \\ &\quad + {\frac{m x_{n(P)}\lambda} {\lambda_2({\user2{x}},k,m)}} T_E({\user2{x}} - {\user2{e}}_{n(P)}, k-1, m + 1 ) \\ & \quad + \frac{m N_R^{[{\user2{x}},k]} \lambda}{\lambda_2({\user2{x}},k,m)} T_E({\user2{x}}, k-1, m+1) \\ & \quad + { \frac{m ( N + 1 - k - m ) \lambda} {\lambda_2({\user2{x}},k,m)}} T_E({\user2{x}}, k, m + 1 ),\\ \end{aligned} $$

(10)

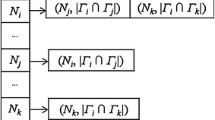
where $T_E({\user2{x}},0,m) = T_E({\user2{x}},N+2-m,m) = 0.$ Recall that, for each m ($m=0,2,3,\ldots,N+1$), states ${{\user2{x}} \in {\mathcal{X}}_P(m)}$ of spreaders are labeled in ascending order of $N_S^{[{\user2{x}}]}.$ For a given m, we denote the lth (${l=1,2,\ldots,|{\mathcal{X}}_P(m)|}$) element in ${{\mathcal{X}}_P(m)}$ by ${\user2{x}}^{[l]} = (x_1^{[l]}, x_2^{[l]}, \ldots, x_{n(P)}^{[l]}).$ As a result, we can compute $\hbox{E}[T_E]=T_E({\user2{e}}_1,1,0)$ by the backward recursive procedure given in Fig. 23.

Fig. 23

Backward recursion to compute E[T _E ]

Appendix 4: Mean accumulated number of messages in the system

The offered load O _L and the mean number E[N _I ] of transmissions of information about the message are given in terms of $R({\user2{e}}_1,1,0),$ which can be computed as follows. We define $R({\user2{x}},k,m)$ ($m=0,2,3,\ldots,N+1,$ $({\user2{x}},k,m) \in {\mathcal{S}}_P(m))$ as

$$R({\user2{x}},k,m) = \hbox{E}\left[\int\limits_0^{T_E} K(t) dt \mid {\user2{Z}}(0) = ({\user2{x}},k,m) \right].$$

Similar to $T_E({\user2{x}},k,m),$ it is easy to see that $R({\user2{x}},k,0)$ ($N_S^{[{\user2{x}}]} \le k \le N$) satisfies

$$\begin{aligned} R({\user2{x}},k,0) &= \frac{k} {\lambda_1({\user2{x}},k,0)} + \sum^{n(P)-1}_{j=1} \frac{N_R^{[{\user2{x}},k]} x_j \lambda} { \lambda_1({\user2{x}},k,0)} R({\user2{x}}_j^{\prime},k,0) \\ & \quad + \sum^{n(P)-1}_{j=1} { \frac{( N - k ) x_j \lambda} {\lambda_1({\user2{x}},k,0)}} R({\user2{x}}_j^{\prime},k+1,0) \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{x_j \lambda} { \lambda_1({\user2{x}},k,0)} R({\user2{x}} - {\user2{e}}_j, k - 1, 2) \\ & \quad + {\frac{(N-k) x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} R({\user2{x}},k+1,0) \\ & \quad + {\frac{x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} R({\user2{x}} - {\user2{e}}_{n(P)}, k - 1, 2) \\ & \quad + \frac{N_R^{[{\user2{x}},k]} \lambda}{\lambda_1 ({\user2{x}},k,0)} R({\user2{x}}, k-1, 2), \\ \end{aligned}$$

where $R({\user2{x}},N+1,0) = R({\user2{x}},0,0) = R({\bf 0},k,0) = 0$. Also, $R({\user2{x}},k,m)$ ($N_S^{[{\user2{x}}]} \leq k \leq N-1,$ 2 ≤ m ≤ N, k + m ≤ N + 1) satisfies

$$\begin{aligned} &{R({\user2{x}},k,m)} \\ &\quad= \frac{k}{\lambda_2({\user2{x}},k,m)} + \sum^{n(P)-1}_{j=1} { \frac{N_R^{[{\user2{x}},k]} x_j \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}}_j^{\prime},k,m) \\ &\quad + \sum^{n(P)-1}_{j=1} { \frac{( N + 1 - k - m) x_j \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}}_j^{\prime},k+1,m) \\ &\quad + \sum^{n(P)-1}_{j=1} { \frac{m x_j \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}} - {\user2{e}}_j, k - 1, m + 1) \\ & \quad+ { \frac{( N + 1 - k - m ) x_{n(P)} \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}}, k + 1, m ) \\ & \quad + { \frac{m x_{n(P)} \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}} - {\user2{e}}_{n(P)}, k-1, m + 1 ) \\ & \quad + { \frac{m N_R^{[{\user2{x}},k]} \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}}, k-1, m + 1 ) \\ & \quad + { \frac{m ( N + 1 - k - m ) \lambda} {\lambda_2({\user2{x}},k,m)}} R({\user2{x}}, k, m + 1 ), \\ \end{aligned}$$

where $R({\user2{x}},0,m) = R({\user2{x}},N+2-m,m) =0.$ Therefore $R({\user2{e}}_1,1,0)$ can be computed by the backward recursion in Fig. 23, where $T_E({\user2{x}}^{[l]}, k, m)$ is replaced by $R({\user2{x}}^{[l]}, k, m)$.

Appendix 5: Mean number of message copy transmissions

Let N _D denote the accumulated number of message copy transmissions till extinction. We then define $N_D({\user2{x}},k,m)$ (${m=0,2,3,\ldots,N+1,\,({\user2{x}},k,m) \in {\mathcal{S}}_P(m)}$) as

$$N_D({\user2{x}},k,m) = \hbox{E}[N_D \mid {\user2{Z}}(0)=({\user2{x}},k,m)].$$

It then follows from Table 2 that $N_D({\user2{x}},k,0)$ ($N_S^{[{\user2{x}}]} \le k \le N$) satisfies

$$\begin{aligned} &{N_D({\user2{x}},k,0)} \; \\ &\quad= \sum^{n(P)-1}_{j=1} \frac{N_R^{[{\user2{x}},k]} x_j \lambda} { \lambda_1({\user2{x}},k,0)} N_D({\user2{x}}_j^{\prime},k,0) \\ &\quad + \sum^{n(P)-1}_{j=1} { \frac{( N - k ) x_j \lambda} {\lambda_1({\user2{x}},k,0)}} \{ 1 + N_D({\user2{x}}_j^{\prime}, k+1,0) \} \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{ x_j \lambda} { \lambda_1({\user2{x}},k,0)} N_D({\user2{x}} - {\user2{e}}_j, k-1, 2)\\ & \quad + {\frac{(N-k) x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} \{ 1 + N_D({\user2{x}},k+1,0) \} \\ & \quad + {\frac{x_{n(P)} \lambda} { \lambda_1 ({\user2{x}},k,0)}} N_D({\user2{x}} - {\user2{e}}_{n(P)}, k-1, 2) \\ & \quad + \frac{N_R^{[{\user2{x}},k]} \lambda}{\lambda_1 ({\user2{x}},k,0)} N_D({\user2{x}}, k-1, 2), \\ \end{aligned}$$

where $N_D({\user2{x}},N+1,0) = N_D({\user2{x}},0,0) = N_D({\bf 0},k,0) = 0$. Also, it follows from Table 3 that $N_D({\user2{x}},k,m)$ ($N_S^{[{\user2{x}}]} \le k \le N - 1, 2 \le m \le N, k+m \le N+1$) satisfies

$$\begin{aligned} &{N_D({\user2{x}},k,m)}\\ &\quad= \sum^{n(P)-1}_{j=1} \frac{N_R^{[{\user2{x}},k]} x_j \lambda}{\lambda_2({\user2{x}},k,m)} N_D({\user2{x}}_j^{\prime},k,m) \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{( N + 1 - k - m) x_j \lambda}{\lambda_2({\user2{x}},k,m)} \{ 1 + N_D({\user2{x}}_j^{\prime}, k+1,m) \} \\ & \quad + \sum^{n(P)-1}_{j=1} \frac{m x_j \lambda}{\lambda_2({\user2{x}},k,m)} N_D({\user2{x}}-{\user2{e}}_j, k-1, m+1) \\ & \quad + \frac{(N+1-k-m) x_{n(P)} \lambda}{\lambda_2({\user2{x}},k,m)} \{ 1 + N_D({\user2{x}}, k+1, m) \} \\ & \quad + {\frac{m x_{n(P)} \lambda} {\lambda_2({\user2{x}},k,m)}} N_D({\user2{x}} - {\user2{e}}_{n(P)}, k-1, m + 1 ) \\ & \quad + \frac{m N_R^{[{\user2{x}},k]} \lambda}{\lambda_2({\user2{x}},k,m)} N_D({\user2{x}}, k-1, m+1) \\ & \quad + {\frac{m ( N + 1 - k - m ) \lambda} {\lambda_2({\user2{x}},k,m)}} N_D({\user2{x}}, k, m + 1 ), \\ \end{aligned}$$

where $N_D({\user2{x}},0,m) = N_D({\user2{x}},N+2-m,m) = 0.$ Therefore $\hbox{E}[N_D] = N_D({\user2{e}}_1,1,0)$ can be computed by the backward recursive procedure in Fig. 23, where $T_E({\user2{x}}^{[l]},k,m)$ is replaced by $N_D({\user2{x}}^{[l]},k,m)$.