An auction-based approach for spectrum leasing in cooperative cognitive radio networks: when to lease and how much to be leased

Abstract

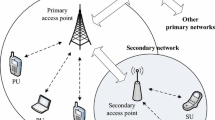
The problem of resource allocation in a spectrum leasing scenario in cooperative cognitive radio networks is addressed. The system model consists of a number of primary user (PU) pairs and a secondary user (SU) pair. The SU pair allocates the whole its transmission power in a portion of transmission frame to relay the primary signals. In return, the PU pairs lease their unused portion of transmission frame to the SU pair. In this way, the PU pairs take advantage of their unused portion of time to gain savings in their transmission power. However, a few important questions must be answered: When to lease and how much to be leased. We determine when is beneficial for PUs to lease their unused spectrum portion to the SU and how much of PUs’ resources is optimum to be leased. An efficient auction mechanism is proposed and the existence and uniqueness of the Nash Equilibrium (NE) for the proposed auction game is proved. Since the NE is the solution of a set of fixed point problems, two iterative algorithms, synchronous and asynchronous schemes, are proposed to reach the NE in an iterative manner and their convergence to the fixed point is also proved. Finally, the proposed auction is extended to a network with multiple secondary user pairs. Simulation results acknowledge the more efficient utilization of resources as a result of implementing the proposed auction based resource allocation.

Appendices

Appendix 1: Proof of Proposition 1

We need to set the derivative of the utility to zero:

$$ \begin{aligned} & \frac{{W{P_{PT,i}}{{\left| {{h_{ST,i}}} \right|}^2}{{\left| {{{{{\bf h}^{\prime}}}_i}{{\bf x}_{PT,i}}} \right|}^2}\left( {{\sigma^2} + {P_{PT,i}}{{\left| {{{{{\bf h}^{\prime}}}_i}{{\bf x}_{PT,i}}} \right|}^2}} \right)}}{{2\ln 2\left( {{\sigma^2} + {P_{PT,i}}{{\left| {{{{{\bf h}^{\prime}}}_i}{{\bf x}_{PT,i}}} \right|}^2} + {P_{ST,i}}{{\left| {{h_{ST,i}}} \right|}^2}} \right)}} \\ & \times \frac{1} {{\left[ {{\sigma^2}\left( {1 + \gamma_i^{(1)}} \right)\left( {{\sigma^2} + {P_{PT,i}}{{\left| {{{{{\bf h}^{\prime}}}_i}{{\bf x}_{PT,i}}} \right|}^2} + {P_{ST,i}}{{\left| {{h_{ST,i}}} \right|}^2}} \right) + {P_{PT,i}}{P_{ST,i}}{{\left| {{{{{\bf h}^{\prime}}}_i}{{\bf x}_{PT,i}}} \right|}^2}{{\left| {{h_{ST,i}}} \right|}^2}} \right]}} \\ & - \frac{\beta }{{P_{ST}}} =0. \end{aligned} $$

(36)

At last, the optimum value of the cooperative transmission power of the SU for PU i, ${\bar P_{ST,i}}$, can be calculated as given in (20), (21) and (22) and therefore the maximum utility of the i-th PU, as a result of cooperation with SU, can be written as in Eq. (19) and the proposition is proved.

Appendix 2: Proof of Proposition 2

Assume that $\left[ {\beta_i^{(2)},\beta_i^{(1)}} \right]$ is not strictly decreasing with $\beta \in \left[ {\beta_i^{(2)},\beta_i^{(1)}} \right]$. Then there must exist a β ₁ < β ₂, such that ${f_i}\left( {{\beta_1}} \right) < {f_i}\left( {{\beta_2}} \right)$, i.e. ${U_i}\left( {P_{ST,i}^*\left( {{\beta_1}} \right),{\beta_1}} \right) \leq {U_i}\left( {P_{ST,i}^*\left( {{\beta_2}} \right),{\beta_2}} \right)$. However, optimality of ${\bar P_{ST,i}}(\beta)$ results in ${U_i}\left( {P_{ST,i}^*\left( {{\beta_1}} \right),{\beta_1}} \right) \geq {U_i}\left( {P_{ST,i}^*\left( {{\beta_2}} \right),{\beta_2}} \right)$ and we have arrived to a contradiction, which verifies that f _i (β) is strictly decreasing with $\beta \in \left[ {\beta_i^{(2)},\beta_i^{(1)}} \right]$.

Appendix 3: Proof of Proposition 3

The best bid of PU i, b ^* _i , can be calculated according to the following:

$$ {\bar P_{ST,i}} = \frac{{b_i^*}}{{\left({\sum\nolimits_{k \in {{\fancyscript{S}}_{PU}}}{{b_k} + \lambda}}\right)}}{P_{ST}}. $$

(37)

Thus, b ^* _i can be written as

$$ b_i^* = \frac{{{{\bar P}_{ST,i}}}}{{{P_{ST}} - {{\bar P}_{ST,i}}}}\sum\limits_{k \in {{\fancyscript{S}}_{PU}},k \ne i} {{b_k}}. $$

(38)

Recall that f _i (β) is strictly increasing over $\left( {0,\beta_i^{(1)}} \right)$, with ${f_i}\left( {\beta_i^{(1)}} \right) < 0$. Thus, using a search method (like bisection method) it is possible to find a transmission frame portion ${\bar \beta_i} \in \left({0,\beta_i^{(1)}}\right)$, such that ${f_i}\left({{{\bar \beta }_i}} \right)=0$. Then for any transmission frame portion $\beta > {\bar \beta_i}$, we have U ^max _i  < 0, which implies that b ^* _i  = 0, and the proposition is proved.