Characterising the Pareto frontier of multiple access rate region: a study on the effect of decoding order on achievable performance

Abstract

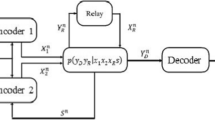
For a multiple access channel, each user has its own power constraint. However, when a multiple access channel is being considered as the dual of a broadcast channel, it must exploit the additional freedom in power allocation and the constraint should be a sum power constraint. Duality helps us to transform the non-convex problems in a broadcast channel to convex problems in a multiple access channel. This helps to solve sum-rate optimisation problems with linear power constraints. However, maximising the sum-rate does not completely characterise the entire rate region boundary, formally called as the Pareto frontier. This work first reviews some of the existing results of polymatroid formulation from the Pareto optimality perspective and then proposes a complete characterisation of the Pareto frontier to show its relationship with the sum-rate optimisation problem. The significance of decoding order on the achievable rate region is considered. The work also shows some of the decoding orders to be suboptimal in Pareto sense and proposes an algorithm to find the correct decoding order based on power allocation. Simulation results are presented to support the theoretical arguments.

Appendix

Let $f(\mathbf{x}): \mathcal{F}\rightarrow\mathbb{R}$ be a concave function where ${\mathcal {F}}\subseteq {{\mathbb {R}}}^n$ is a convex set. Now consider $m$ additional affine constraints ${\mathbf {Ax}}={\mathbf {y}}$ for some ${\mathbf {A}}\in {{\mathbb {R}}}^{m\times n}$ and ${\mathbf {y}}\in {{\mathbb {R}}}^m$. Denote the optimal value as $\phi \left( {\mathbf {y}}\right)$.

$$\begin{aligned} \phi \left( {\mathbf {y}}\right) \equiv \max _{{\mathbf {x}}}f \left( {\mathbf {x}}\right) \end{aligned}$$

subject to ${\mathbf {x}}\in {\mathcal {F}}$ and ${\mathbf {Ax}}={\mathbf {y}}$. Let ${\mathcal {Y}}\subseteq {{\mathbb {R}}}^m$ be the set of ${\mathbf {y}}$ for which the problems (with additional constraints) are feasible.

Theorem 5

$\phi :{\mathcal {Y}}\rightarrow {{\mathbb {R}}}$ is a concave function on its domain.

Proof

In presence of the additional constraints, the problem is a convex optimisation problem. Now for the additional constraint ${\mathbf {Ax}}={\mathbf {y}}_1$, let the solution be ${\mathbf {x}}_1^*$ and similarly for ${\mathbf {Ax}}={\mathbf {y}}_2$, let the solution be ${\mathbf {x}}_2^*$. Then

$$\begin{aligned} \phi \left( {\mathbf {y}}_1\right)&= f({\mathbf {x}}_1^*)\\ \phi \left( {\mathbf {y}}_2\right)&= f({\mathbf {x}}_2^*) \end{aligned}$$

and from feasibility conditions ${\mathbf {Ax}}_1^*={\mathbf {y}}_1$ and ${\mathbf {Ax}}_2^*={\mathbf {y}}_2$. Now for any $\alpha \in [0, 1]$, consider the point

$$\begin{aligned} \alpha {\mathbf {x}}_1^*+(1-\alpha ){\mathbf {x}}_2^*\in {\mathcal {F}} \end{aligned}$$

which is a feasible point satisfying the constraints

$$\begin{aligned} {\mathbf {Ax}}=\alpha {\mathbf {y}}_1+(1-\alpha ){\mathbf {y}}_2 \end{aligned}$$

So ${\mathcal {Y}}$ is a convex region. Moreover

$$\begin{aligned}&\phi \left( \alpha {\mathbf {y}}_1+(1-\alpha ){\mathbf {y}}_2\right) \\&\ge\,f(\alpha {\mathbf {x}}_1^*+(1-\alpha )\,{\mathbf {x}}_2^*)\\&\ge\,\alpha f({\mathbf {x}}_1^*)+(1-\alpha )\,f({\mathbf {x}}_2^*)\\&=\alpha \phi ({\mathbf {y}}_1)+(1-\alpha )\phi ({\mathbf {y}}_2) \end{aligned}$$

where the second inequality follows from concavity of $f$.