Skip to main content
SpringerLink
Log in

Filtering effects on the synchronization and error performance of promising wireless chaos-based secure communications

  • Published:
Wireless Networks Aims and scope Submit manuscript

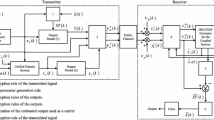
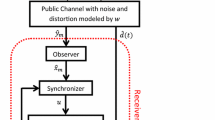
Abstract

Synchronization is one of the most challenging topics involved in the development of promising chaos-based secure communication (CBSC) for wireless applications due its direct impact on the error performance and reliability. In this paper, effects of filtering chaotic signals on the synchronization and average bit-error-rate (BER) of CBSC caused by the limited bandwidth of realistic wireless communication channels and detection requirements are investigated. To overcome the possible drawbacks of filtering process, two efficient methods called chaotic signal reconstruction technique (CSRT) and pre-filtering chaos technique (PFCT) are proposed. The well known double scroll chaotic attractor generated from Chua’s circuit is utilized at both transmit and receive nodes as in a drive–response configuration with identical synchronization, and a mathematical model of single-pole low-pass filter is employed in this study. Over Rayleigh fading channel and wide range of filter cut-off frequency (η), simulation results show that as η decreased, lesser than the bandwidth of utilized chaotic signal, the synchronization mean squared error is increased due to the resulting high distortion in the attractor’s ordinary state-space. Consequently, system BER performance is degraded significantly leading to increased possibility of communication link failure. When CSRT from received filtered signal and PFCT of drive chaotic signal are utilized, the achieved results are interesting in terms of robust synchronization and error performance, and provide potential step towards wide adoption of CBSC in future applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Yang, J., & Zhu, F. (2013). Synchronization for chaotic systems and chaos-based secure communications via both reduced-order and step-by-step sliding mode observers. Communications in Nonlinear Science and Numerical Simulation, 18(4), 926–937.

    Article  MathSciNet  MATH  Google Scholar 

  2. Eisencraft, M., Fanganiello, R., Grzybowski, J., Soriano, D., Attux, R., Batista, A., et al. (2012). Chaos-based communication systems in non-ideal channels. Communications in Nonlinear Science and Numerical Simulation, 17(12), 4707–4718.

    Article  Google Scholar 

  3. Bhatnagar, G., & JonathanWu, Q. (2012). Chaos-based security for fingerprint data during communication and transmission. IEEE Transactions on Instrumentation and Measurement, 61(4), 876–887.

    Article  Google Scholar 

  4. Hou, Y., Chen, H., Chang, J., Yan, J., & Liao, T. (2012). Design and implementation of the Sprott chaotic secure digital communication systems. Applied Mathematics and Computation, 218(24), 11799–11805.

    Article  MathSciNet  Google Scholar 

  5. Tam, W., Lau, F., & Tse, C. (2004). A multiple access scheme for chaos-based digital communication systems utilizing transmitted reference. IEEE Transactions on Circuits and Systems-I: Regular Papers, 51(9), 1868–1878.

    Article  Google Scholar 

  6. Puebla, H., & Alvarez-Ramirez, J. (2001). Stability of inverse-system approaches in coherent chaotic communication. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 48(12), 1413–1423.

    Article  Google Scholar 

  7. Corron, N., & Hahs, D. (1997). A new approach to communications using chaotic signals. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 44(5), 373–382.

    Article  MATH  Google Scholar 

  8. Hayes, S., Grebogi, C., & Ott, E. (1993). Communicating with chaos. Physical Review Letters, 70(20), 3031–3034.

    Article  Google Scholar 

  9. Pecora, L., & Carroll, T. (1990). Synchronization in chaotic systems. Physical Review Letters, 64(8), 821–824.

    Article  MathSciNet  MATH  Google Scholar 

  10. Cuomo, K., & Oppenheim, A. (1993). Circuit implementation of syncronized chaos with applications to communications. Physical Review Letters, 71(1), 65–68.

    Article  Google Scholar 

  11. Dedieu, H., Kennedy, M., & Hasler, M. (1993). Chaos shift keying: Modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits. IEEE Transactions on Circuits and Systems-II: Analog and Digital Signal Processing, 40(10), 634–642.

    Article  Google Scholar 

  12. Al-Hussaibi, W. (2013). Impact of filtering chaotic signals on secure wireless communication systems based Chua’s circuit. Proceedings of IIT’13 (pp. 89–94). Al Ain, Abu Dhabi, UAE.

  13. Chang, W. (2009). Digital secure communication via chaotic systems. Digital Signal Processing, 19(4), 693–699.

    Article  Google Scholar 

  14. Zaher, A. (2009). An improved chaos-based secure communication technique using a novel encryption function with an embedded cipher key. Chaos, Solitons & Fractals, 42(5), 2804–2814.

    Article  MATH  Google Scholar 

  15. Murali, K., Yu, H., Varadan, V., & Leung, H. (2001). Secure communication using a chaos based signal encryption scheme. IEEE Transactions on Consumer Electronics, 47(4), 709–714.

    Article  Google Scholar 

  16. Kiani-B, A., Fallahi, K., Pariz, N., & Leung, H. (2009). A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter. Communications in Nonlinear Science and Numerical Simulation, 14(3), 863–879.

    Article  MathSciNet  MATH  Google Scholar 

  17. Changchien, S.-K., Huang, C.-K., Nien, H.-H., & Shieh, H.-W. (2009). Synchronization of the chaotic secure communication system with output state delay. Chaos, Solitons & Fractals, 39(4), 1578–1587.

    Article  MathSciNet  MATH  Google Scholar 

  18. Zheng, G., Boutat, D., Floquet, T., & Barbot, J. (2009). Secure communication based on multi-input multi-output chaotic system with large message amplitude. Chaos, Solitons & Fractals, 41(3), 1510–1517.

    Article  Google Scholar 

  19. Jung, P., Baier, P., & Steil, A. (1993). Advantages of CDMA and spread spectrum techniques over FDMA and TDMA in cellular mobile radio applications. IEEE Transactions on Vehicular Technnology, 42(3), 357–364.

    Article  Google Scholar 

  20. Kolumban, G., Kennedy, M., & Chua, L. (1997). The role of synchronization in digital communications using chaos-part I: Fundamentals of digital communications. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 44(10), 927–936.

    Article  MathSciNet  Google Scholar 

  21. Kolumban, G., Kennedy, M., & Chua, L. (1998). The role of synchronization in digital communications using chaos-part II: Chaotic modulation and chaotic synchronization. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 45(11), 1129–1140.

    Article  MathSciNet  MATH  Google Scholar 

  22. Kolumban, G., & Kennedy, M. (2000). The role of synchronization in digital communications using chaos-part III: Performance bounds for correlation receivers. IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, 47(12), 1673–1683.

    Article  MathSciNet  MATH  Google Scholar 

  23. Badii, R., Broggi, G., Derieghetti, B., & Ravani, M. (1988). Dimension increase in filtered chaotic signals. Physical Review Letters, 60(11), 979–982.

    Article  Google Scholar 

  24. Mitschke, F., Moller, M., & Lange, W. (1988). Measuring filtered chaotic signals. Physical Review A, 37(11), 4518–4521.

    Article  Google Scholar 

  25. Chennaoui, A., Pawelzik, K., & Liebert, W. (1990). Attractor reconstruction from filtered chaotic time series. Physical Review A, 41(8), 4151–4159.

    Article  Google Scholar 

  26. Rosenstein, M., & Collins, J. (1994). Visualizing the effects of filtering chaotic signals. Computer and Graphics, 18(4), 587–592.

    Article  Google Scholar 

  27. Pecora, L., & Carroll, T. (1996). The effect of filtering on communication using synchronized chaotic circuits. Proceedings of IEEE ISCAS, 3, 174–177.

    Google Scholar 

  28. Zhu, L., Lai, Y., Hoppensteadt, F., & Bollt, E. (2003). Numerical and experimental investigation of the effect of filtering on chaotic symbolic dynamics. Chaos, 13(1), 410–419.

    Article  Google Scholar 

  29. Harb, A., Al-Hussaibi, W., & Khadra, L. (2003). Effects of filtering chaotic signals of power electronic circuit. International Journal of Modeling and Simulation, 23(2), 129–134.

    Google Scholar 

  30. Matsumoto, T., Chua, L., & Komuro, M. (1985). The double scroll. IEEE Transactions on Circuits and Systems, 32(8), 798–818.

    Article  MathSciNet  Google Scholar 

  31. Chua, L., & Lin, G. (1990). Canonical realization of Chua’s circuit family. IEEE Transactions on Circuits and Systems, 37(7), 885–902.

    Article  MathSciNet  MATH  Google Scholar 

  32. Cruz-Hernandez, C., & Romero-Haros, N. (2008). Communicating via synchronized time-delay Chua’s circuits. Communications in Nonlinear Science and Numerical Simulation, 13(3), 645–659.

    Article  MathSciNet  MATH  Google Scholar 

  33. Gamez-Guzman, L., Cruz-Hernandez, C., Lopez-Gutierrez, R., & Garcia-Guerrero, E. (2009). Synchronization of Chua’s circuits with multi-scroll attractors: Application to communication. Communications in Nonlinear Science and Numerical Simulation, 14(6), 2765–2775.

    Article  Google Scholar 

  34. Cheng, C. (2012). Robust synchronization of uncertain chaotic systems subject to noise and its application to secure communication. Applied Mathematics and Computation, 219(5), 2698–2712.

    Article  MathSciNet  MATH  Google Scholar 

  35. Mata-Machuca, J., Martinez-Guerra, R., Aguilar-Lopez, R., & Aguilar-Ibanez, C. (2012). A chaotic system in synchronization and secure communications. Communications in Nonlinear Science and Numerical Simulation, 17(4), 1706–1713.

    Article  MathSciNet  Google Scholar 

  36. Al-Hussaibi, W., & Ali, F. (2012). Generation of correlated Rayleigh fading channels for accurate simulation of promissing wireless communication systems. Elsevier: Simulation Modelling Practice and Theory, 25(4), 56–72.

    Google Scholar 

  37. Sklar, B. (1997). Rayleigh fading channels in mobile digital communication systems, part I: Characterization. IEEE Communications Magazine, 35(7), 90–100.

    Article  Google Scholar 

  38. Albano, A., Muench, J., & Schwartz, C. (1988). Singular-value decomposition and the Grassberger–Procaccia algorithm. Physical Review A, 38(6), 3017–3026.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ministry of Higher Education and Scientific Research, Baghdad, Iraq

    Walid A. Al-Hussaibi

Authors
  1. Walid A. Al-Hussaibi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Walid A. Al-Hussaibi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Al-Hussaibi, W.A. Filtering effects on the synchronization and error performance of promising wireless chaos-based secure communications. Wireless Netw 21, 1957–1967 (2015). https://doi.org/10.1007/s11276-015-0897-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11276-015-0897-0

Keywords

Search

Navigation