Efficient power control for half-duplex relay based D2D networks under sum power constraints

Abstract

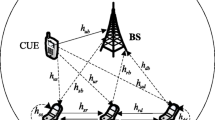
Device-to-device (D2D) communications provide an effective way to improve local services in cellular networks which allow close-by users to communicate directly. Considering cooperative relay (CR) can achieve high spectrum and energy efficiency, this paper proposes a novel CR-based D2D communication scheme, referred to as CR-D2D, which allows a D2D link to underlay a cellular downlink by assigning a D2D transmitter as a half-duplex relay to assist cellular downlink communication. To maximize the achievable rates of D2D users and meanwhile to meet the minimum rate requirements of cellular users, transmission powers allocated to the base station (BS) and to the D2D transmitter are both optimized under the sum power constraint, while existing works usually perform the optimization at the BS and at the D2D transmitter independently. The simulation results show that the proposed CR-D2D scheme outperforms traditional cellular communication scheme in system throughput and in spectrum utilization efficiency.

Appendices

Appendix 1

Proof of Lemma 1

The substitution of $\gamma_{{\mathcal{R},2}}^{\text{D}}$ [defined in Eq. (12)] into $\mathcal{C}_{2}^{\text{D}}$ [defined in Eq. (14)] yields

$$\mathcal{C}_{2}^{\text{D}} = \frac{1}{4}W\log_{2} \left( {1 + \frac{{\left( {1 - \theta } \right)p_{\mathcal{R}}^{\text{D}} \eta_{{\mathcal{R},2}} }}{{\theta p_{\mathcal{R}}^{\text{D}} \eta_{{\mathcal{R},2}} + 1}}} \right)$$

(22)

Taking the first-order partial derivative of $\mathcal{C}_{2}^{\text{D}} \left( {p_{\mathcal{R}}^{\text{D}} ,\theta } \right)$ with respect to θ, we can get

$$\frac{{\partial \mathcal{C}_{2}^{\text{D}} \left( {p_{\mathcal{R}}^{\text{D}} ,\theta } \right)}}{\partial \theta } = - \frac{W}{4\ln 2}\frac{\theta }{{\theta p_{\mathcal{R}}^{\text{D}} \gamma_{{\mathcal{R},2}} + 1}} \le 0$$

(23)

That means $\mathcal{C}_{2}^{\text{D}}$ monotonically decreases as θ increases. Thus, Lemma 1 follows.

Appendix 2

Proof of Proposition 1

As $\gamma_{{\mathcal{R},1}}^{\text{D}} \ge \gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}}$, we have

$$\begin{aligned} \gamma_{{\mathcal{B},\mathcal{R},1}}^{\text{D}} & =\, \hbox{min} \left\{ {\gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}} ,\gamma_{{\mathcal{R},1}}^{\text{D}} } \right\} = \gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}} \\ & \Rightarrow \left( {\bar{P} - p_{\mathcal{R}}^{\text{D}} } \right)\gamma_{{\mathcal{B},\mathcal{R}}} = G \\ \end{aligned}$$

(24)

To satisfy the CBR requirement of UE₁, we first solve equations $p_{\mathcal{B}}^{\text{D}} + p_{\mathcal{R}}^{\text{D}} { = }\bar{P}$ in (15-2) and (24). and we can get

$$\hat{p}_{\mathcal{B}}^{\text{D}} = \frac{G}{{\eta_{{\mathcal{B},\mathcal{R}}} }}\quad {\text{and}}\quad \hat{p}_{\mathcal{R}}^{\text{D}} = \hbox{max} \left( {0,\bar{P} - \frac{G}{{\eta_{{\mathcal{B},\mathcal{R}}} }}} \right)$$

(25)

Next, we further substitute Eqs. (25) and (12) into $\gamma_{{\mathcal{R},1}}^{\text{D}} \ge \gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}}$. We get

$$\theta \ge \frac{{\eta_{{\mathcal{B},\mathcal{R}}} }}{{\eta_{{\mathcal{R},1}} }}\frac{{ - \left( {\hat{p}_{\mathcal{R}}^{\text{D}} } \right)^{2} \eta_{{\mathcal{R},1}} + \hat{p}_{\mathcal{R}}^{\text{D}} \left( {\bar{P}\eta_{{\mathcal{R},1}} - 1} \right) + \bar{P}}}{{ - \left( {\hat{p}_{\mathcal{R}}^{\text{D}} } \right)^{2} \eta_{{\mathcal{B},\mathcal{R}}} + \hat{p}_{\mathcal{R}}^{\text{D}} \left( {\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} + 1} \right)}}$$

(26)

From Lemma 1, we know that $\mathcal{C}_{2}^{\text{D}}$ monotonically decreases as θ increases. Since 0 ≤ θ < 1, we can give the optimal θ to maximize the achievable rate for the D2D link as

$$\hat{\theta } = \hbox{max} \left( {0,\,\hbox{min} \left( {1,\frac{{\eta_{{\mathcal{B},\mathcal{R}}} }}{{\eta_{{\mathcal{R},1}} }}\frac{{ - \left( {\hat{p}_{\mathcal{R}}^{\text{D}} } \right)^{2} \eta_{{\mathcal{R},1}} + \hat{p}_{\mathcal{R}}^{\text{D}} \left( {\bar{P}\eta_{{\mathcal{R},1}} - 1} \right) + \bar{P}}}{{ - \left( {\hat{p}_{\mathcal{R}}^{\text{D}} } \right)^{2} \eta_{{\mathcal{B},\mathcal{R}}} + \hat{p}_{\mathcal{R}}^{\text{D}} \left( {\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} + 1} \right)}}} \right)} \right)$$

(27)

Appendix 3

Proof of proposition 2

When $\gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}} \ge \gamma_{{\mathcal{R},1}}^{\text{D}}$, we have

$$\begin{aligned} \gamma_{{\mathcal{B},\mathcal{R},1}}^{\text{D}} & =\, \hbox{min} \left\{ {\gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}} ,\gamma_{{\mathcal{R},1}}^{\text{D}} } \right\} = \gamma_{{\mathcal{R},1}}^{\text{D}} \\ & \Rightarrow \frac{{\theta p_{\mathcal{R}}^{\text{D}} \gamma_{{\mathcal{R},1}} }}{{\left( {1 - \theta } \right)p_{\mathcal{R}}^{\text{D}} \gamma_{{\mathcal{R},1}} + 1}} = G \\ \end{aligned}$$

(28)

To satisfy the CBR requirement of UE₁, we first solve equations $p_{\mathcal{B}}^{\text{D}} + p_{\mathcal{R}}^{\text{D}} { = }\bar{P}$ [defined in Eq. (15-2)] and (28). Then we can get

$$\hat{p}_{\mathcal{B}}^{\text{D}} = \hbox{max} \left( {0,\bar{P} - \frac{1}{{\eta_{{\mathcal{R},1}} }}\frac{G}{{\hat{\theta }\left( {G + 1} \right) - G}}} \right)\quad {\text{and}}\quad \hat{p}_{\mathcal{R}}^{\text{D}} = \hbox{max} \left( {0,\,\frac{1}{{\eta_{{\mathcal{R},1}} }}\frac{G}{{\hat{\theta }\left( {G + 1} \right) - G}}} \right)$$

(29)

where the optimal $\hat{\theta }$ remains unknown.Next, to find the optimal $\hat{\theta }$, we substitute the expressions for $\gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}}$ [defined in Eq. (9)] and $\gamma_{{\mathcal{R},1}}^{\text{D}}$ [defined in Eq. (12)] into $\gamma_{{\mathcal{B},\mathcal{R}}}^{\text{D}} \ge \gamma_{{\mathcal{R},1}}^{\text{D}}$. We can get

$$\left( {\bar{P} - p_{\mathcal{R}}^{\text{D}} } \right)\eta_{{\mathcal{B},\mathcal{R}}} \ge \frac{{\theta p_{\mathcal{R}}^{\text{D}} \eta_{{\mathcal{R},1}} }}{{\left( {1 - \theta } \right)p_{\mathcal{R}}^{\text{D}} \eta_{{\mathcal{R},1}} + 1}}$$

(30)

By further substituting $\hat{p}_{\mathcal{R}}^{\text{D}}$ given in Eq. (29) into inequality (30), we can convert inequality (30) into the following quadratic inequality with only one unknown variable θ.

$$f\left( \theta \right) = A\theta^{2} + B\theta + C \ge 0$$

(31)

where the value of the constants A, B and C are given in Eq. (20).To solve the above quadratic inequality, we first note that

$$\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} > \left( {\bar{P} - p_{\mathcal{R}}^{\text{D}} } \right)\eta_{{\mathcal{B},\mathcal{R}}} = G\quad {\text{and}}\quad \eta_{{\mathcal{R},1}} > \eta_{{\mathcal{B},1}}$$

(32)

The reasonability of $\eta_{{\mathcal{R},1}} > \eta_{{\mathcal{B},1}}$ in (32) is explained as follows. The D2D communication can be invoked only if D2D transmitter ${\text{HN}}_{\mathcal{R}}$ can help satisfy the CBR requirement of the cellular UE, i.e., UE₁. It is essential that CNR $\eta_{{\mathcal{R},1}} > \eta_{{\mathcal{B},1}}$. Otherwise, UE₁ would rather operate in the TC scheme.Adhering to inequalities (32), we can derive that

$$A = \left( {G + 1} \right)\left( {\eta_{{\mathcal{R},1}} } \right)^{2} \left( {\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} - G} \right) > 0$$

(33)

and

$$B^{2} - 4AC = \left( { - \bar{P}G\left( {\eta_{{\mathcal{R},1}} } \right)^{2} \eta_{{\mathcal{B},\mathcal{R}}} + \left( {G\eta_{{\mathcal{R},1}} } \right)^{2} - G\eta_{{\mathcal{R},1}} \eta_{{\mathcal{B},\mathcal{R}}} } \right)^{2} + 8\bar{P}G^{2} \left( {G + 1} \right)\left( {\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} - G} \right)\left( {\eta_{{\mathcal{R},1}} } \right)^{4} \eta_{{\mathcal{B},\mathcal{R}}} > 0$$

(34)

Then, the solution to the quadratic inequality (31) is clearly:

$$\theta \le \theta_{1} = \frac{{ - B - \sqrt {B^{2} - 4AC} }}{2A}\quad {\text{or}}\quad \theta \ge \theta_{2} = \frac{{ - B + \sqrt {B^{2} - 4AC} }}{2A}$$

(35)

We also note that

$$\theta_{1} \theta_{2} = \frac{C}{A} = - \frac{{2\bar{P}G^{2} \eta_{{\mathcal{B},\mathcal{R}}} }}{{\left( {G + 1} \right)\left( {\bar{P}\eta_{{\mathcal{B},\mathcal{R}}} - G} \right)}} < 0$$

(36)

So we can determine that θ ₁ < 0 < θ ₂. From Lemma 1, we know that $\mathcal{C}_{2}^{\text{D}}$ monotonically decreases as θ increases. Since 0 ≤ θ < 1, the optimal θ is obtained as

$$\hat{\theta } = \hbox{max} \left( {0,\hbox{min} \left( {1,\frac{{ - B + \sqrt {B^{2} - 4AC} }}{2A}} \right)} \right)$$

(37)