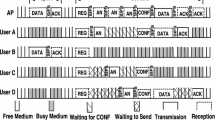
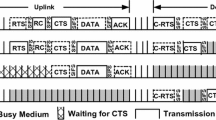
Abstract
In this paper, we consider a carrier sense multiple access based wireless local area network (WLAN) with a successive interference cancellation (SIC) technique. We develop an analytical model to compute the average throughput of a user in a WLAN with the SIC technique in presence of path loss, Rayleigh fading and log-normal shadowing. We then validate the model via simulation. By means of the developed analytical model, we compute the average throughput of a user in WLAN systems without and with the SIC technique and evaluate the throughput gain provided by the SIC technique. We find that the throughput gain provided by the SIC technique is significant. However, the throughput gain varies significantly depending on the parameters of network and wireless channel. We find that the throughput gain provided by the SIC technique increases with increasing the number of users in WLAN, medium access rate of the users and the variance in shadowing and it decreases with increasing the data transmission rate. We also investigate the effect of the decoding capability of the SIC technique on the throughput performance. We find that throughputs obtained with decoding capability of 2 and 3 packets are very close.






Similar content being viewed by others
References
IEEE 802.11 Working Group. (1997). Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specification.
Bianchi, G. (2000). Performance analysis of the IEEE 802.11 distributed coordination function. IEEE Journal on Selected Areas in Communications, 18(3), 535–547.
Zhai, H., Kwon, Y., & Fang, Y. (2004). Performance analysis of IEEE 802.11 MAC protocols in wireless LANs. Wireless Communications and Mobile Computing, 4, 917–931.
Chatzimisios, P., Vitsas, V., & Boucouvalas, A. C. (2003). Throughput and delay analysis of IEEE 802.11 protocol. In Proceedings of IEEE workshop networked appliances, pp. 168–174.
Felemban, E., & Ekici, E. (2011). Single hop IEEE 802.11 DCF analysis revisited: Accurate modeling of channel access delay and throughput for saturated and unsaturated traffic cases. IEEE Transactions on Wireless Communications, 10, 3256–3266.
Lindgren, A., & Almquist, A. (2001). Quality of service schemes for IEEE 802.11—A simulation study. M.S. thesis, Lule University of Technology.
Bai, G., & Williamson, C. (2003). Simulation evaluation of wireless web performance in an IEEE 802.11b classroom area network. In Proceedings of IEEE 3rd international workshop on wireless local networks (WLN), pp. 663–672.
Iyer, A., Rosenberg, C., & Karnik, A. (2009). What is the right model for wireless channel interference? IEEE/ACM Transactions on Networking, 8(5), 2662–2671.
Uddin, M. F., Rosenberg, C., Zhuang, W., Mitran, P., & Girard, A. (2014). Joint routing and medium access control in fixed random access wireless multihop networks. IEEE/ACM Transactions on Networking, 22(1), 80–93.
Jiang, L., & Walrand, J. (2011). Approaching throughput-optimality in a distributed CSMA algorithm: Collisions and stability. IEEE/ACM Transactions on Networking, 19(23), 816–829.
Qian, D., Zheng, D., Zhang, J., Shroff, N. B., & Joo, C. (2013). Distributed CSMA algorithms for link scheduling in multihop MIMO networks under SINR model. IEEE/ACM Transactions on Networking, 21(3), 746–759.
Hadzi-Velkov, Z., & Spasenovski, B. (2002). Capture effect in IEEE 802.11 basic service area under Influence of Rayleigh fading and near/far effect. Proceedings of IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 1, 172–176.
Kim, J. H., & Lee, J. K. (1999). Capture effects of wireless CSMA/CA protocols in Rayleigh and shadow fading channels. IEEE Transactions on Vehicular Technology, 48(4), 1277–1286.
Li, X., & Zeng, Q. (2006). Performance analysis of the IEEE 802.11 MAC protocols over a WLAN with capture effect. Information and Media Technologies, 1, 679–685.
Verdu, S. (1998). Multiuser detection. Cambridge: Cambridge University Press.
Andrews, J. G. (2005). Interference cancellation for cellular systems: A contemporary overview. IEEE Wireless Communications Magazine, 12(2), 19–29.
Johansson, A.-L., & Svensson, A. (1995). Successive interference cancellation in multiple data rate DS/CDMA systems. In Proceedings of IEEE vehicular technology conference, pp. 704–708.
Mitran, P., Rosenberg, C., & Shabdanov, S. (2011). Throughput optimization in wireless multihop networks with successive interference cancellation. In Proceedings of IEEE wireless telecommunications symposium.
Yuan, D., Angelakis, V., Chen, L., Karipidis, E., & Larsson, E. G. (2013). On optimal link activation with interference cancelation in wireless networking. IEEE Transactions on Vehicular Technology, 62(2), 939–945.
Toumpis, S., & Goldsmith, A. (2003). Capacity regions for wireless ad hoc networks. IEEE Transaction on Wireless Communications, 2(4), 736–748.
Seskar, I., Pedersen, K. I., Kolding, T. E., & Holtzman, J. M. (1998). Implementation aspects for successive interference cancellation in DS/CDMA systems. Wireless Networks, 4(6), 447–452.
Sen, S., Santhapuri, N., Choudhury, R. R., & Nelakuditi, S. (2013). Successive interference cancellation: Carving out MAC layer opportunities. IEEE Transactions on Mobile Computing, 12(2), 346–357.
Lv, S., Zhuang, W., & Wang, X. (2011). Link scheduling in wireless networks with successive interference cancellation. Computer Networks, 55(6), 2929–2941.
Goussevskaia, O., & Wattenhofer, R. (2012). Scheduling wireless links with successive interference cancellation. In Proceedings of IEEE ICCCN.
Mollanoori, M., & Ghaderi, M. (2012). On the performance of successive interference cancellation in random access networks. In Proceedings of IEEE SECON.
Yu, Y., & Giannakis, G. B. (2007). High-throughput random access using successive interference cancellation in a tree algorithm. IEEE Transactions on Information Theory, 53(12), 4628–4639.
Zou, M., Chan, S., Vu, H.L., & Ping, L. (2011). Optimal throughput for 802.11 DCF with multiple packet reception. In Proceedings of IEEE on local and computer networks (LCN).
Subaid, M. R., Hasan, M. R., Ahmed, S. Z., & Uddin, M. F. (2013). Performance of successive interference cancellation technique in IEEE 802.11 based WLANs. In Proceedings of IEEE ICIEV, pp. 1–6.
Lv, S., Zhuang, W., Wang, X., Liu, C., Hu, X., Sun, Y., et al. (2012). A performance study of CSMA in wireless networks with successive interference cancellation. In Proceedings of IEEE ICC.
Rao, S. S. (2002). Applied numerical methods for engineers and scientists. Upper Saddle River: Prentice Hall.
Durgin, G. D., Rappaport, T. S., & Xu, H. (1998). Measurements and models for radio path loss and penetration loss in and around homes and trees at 5.85 GHz. IEEE Transactions on Communcations, 46(11), 1484–1496.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Computation of \(P(E_{i,j,k})\)
For considering high transmission power, the value of \(N_0\) is negligible compared to the received power of the AP from any user. Neglecting the effect of \(N_0\) and using (1) in (23), we obtain
where, the events \(E_A\), \(E_B\) and \(E_C\) are given as
Further, applying the condition probability formula, \(P(E_{i,j,k})\) can be written as
Conditioning on \(\underline{\gamma }=\{\gamma _n \quad \forall n\in v\}\) and \(\underline{r}=\{r_n \quad \forall n \in v\}\), \(P(E_C)\), \(P(E_B|E_C)\) and \(P(E_A|E_B, E_C)\) can be written as follows.
where,
From (43), it can be shown that
where,
From (46), one can show that
Replacing \(P[E_A|E_B, E_C]\), \(P[E_B|E_C]\) and \(P[E_C]\) in (41) using (42), (45) and (48), we obtain
where,
and
Averaging over \(\forall \gamma _n, n \in v \setminus \{i,j,k\}\) and \(\forall r_n, n \in v \setminus \{i,j,k\}\), from (49), we obtain
where,
Further, averaging over \(\gamma _i\), \(\gamma _j\) and \(\gamma _k\), from (52), we obtain
Then, averaging over \(r_i\), \(r_j\) and \(r_k\) in (54), \(P(E_{i,j,k})\) can be obtained as
Appendix 2: Computation of \(P(E_{j,k})\)
Similar to (37) and (41), \(P(E_{j,k})\) can be obtained as
where, the events \(E_D\) and \(E_E\) are given by
Similar to (42) and (45), the expressions of \(P(E_E|\underline{\gamma },\underline{r})\) and \(P(E_D|E_E,\underline{\gamma },\underline{r})\) can be derived and by setting their expressions in (56), one can show that
Averaging over \(\forall \gamma _n, n \in v \setminus \{j,k\}\) and \(\forall r_n, n \in v \setminus \{j,k\}\), from (59) it can be shown that
where,
Further, averaging over \(\gamma _j\) and \(\gamma _k\), from (60), we obtain
Again, averaging over \(r_j\) and \(r_k\) in (62), \(P(E_{j,k})\) can be written as
Appendix 3: Computation of \(P(E_k)\)
Similar to (42), one can determine \(P(E_k|\underline{\gamma },\underline{r})\) as
Averaging over \(\forall \gamma _n, n \in v \setminus k\) and \(\forall r_n, n \in v \setminus k\), from (64), we obtain
where,
Further, averaging over \(\gamma _k\) and \(r_k\) in (65), we obtain
Rights and permissions
About this article
Cite this article
Uddin, M.F. Throughput analysis of a CSMA based WLAN with successive interference cancellation under Rayleigh fading and shadowing. Wireless Netw 22, 1285–1298 (2016). https://doi.org/10.1007/s11276-015-1038-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-015-1038-5