Abstract
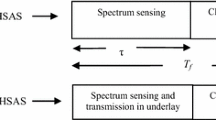
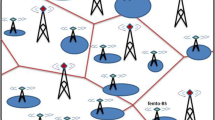
Cognitive radio and small cells are the promising techniques to minimize energy consumption and satisfy the exponentially increasing data rates for the heterogeneous cellular network (HCN). In this paper, a theoretical framework is developed to calculate the outage probability of the HCN based on the opportunistic utilization of the traditional cellular bandwidth and television white space (TVWS) for the cognitive femto base stations. This work investigates overlay, underlay, mixed overlay-underlay based two tiers cognitive HCN. It also investigates the impact of the TVWS in the overlay-TVWS mixed spectrum sharing technique (SST). Tools from stochastic geometry are used to model cognitive HCN. Furthermore, the tier selection probability, average ergodic rate, area spectral efficiency (ASE), and energy efficiency (EE) of the HCN are also calculated for different SSTs. Numerical results show that mixed SST achieves a significant reduction in tier outage probability and total outage probability as compared to underlay and overlay techniques alone. It is also demonstrated that compared to the traditional single tier network, cognitive based HCN can improve the total ASE and EE of the order of \(10^{2}\) and 10, respectively.












Similar content being viewed by others
References
Wang, C.-X., Haider, F., Gao, X., You, X.-H., Yang, Y., Yuan, D., et al. (2014). Cellular architecture and key technologies for 5G wireless communication networks. IEEE Communications Magazine, 52(2), 122–130.
Li, Y., Celebi, H., Daneshmand, M., Wang, C., & Zhao, W. (2013). Energy-efficient femtocell networks: Challenges and opportunities. IEEE Wireless Communications, 20(6), 99–105.
Akyildiz, I. F., Lee, W.-Y., Vuran, M. C., & Mohanty, S. (2006). Next generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Computer Networks, 50(13), 2127–2159.
Oh, J., & Choi, W. (2010). A hybrid cognitive radio system: A combination of underlay and overlay approaches. In IEEE 72nd vehicular technology conference fall (VTC 2010-Fall), 2010, pp. 1–5. IEEE.
Ma, Y., Guo, Y., Niu, K., & Lin, J. (2012). Transmission capacity of secondary networks in hybrid overlaid/underlaid cognitive radio systems. In IEEE 14th international conference on communication technology (ICCT), pp. 397–401. IEEE.
Bansal, G., Hossain, M. J., Bhargava, V. K., & Le-Ngoc, T. (2013). Subcarrier and power allocation for ofdma-based cognitive radio systems with joint overlay and underlay spectrum access mechanism. IEEE Transactions on Vehicular Technology, 62(3), 1111–1122.
Nekovee, M., Irnich, T., & Karlsson, J. (2012). Worldwide trends in regulation of secondary access to white spaces using cognitive radio. IEEE Wireless Communications, 19(4), 32–40.
Baykas, T., Kasslin, M., Cummings, M., Kang, H., Kwak, J., Paine, R., et al. (2012). Developing a standard for tv white space coexistence: Technical challenges and solution approaches. IEEE Wireless Communications, 19(1), 10–22.
Saeed, A., Ibrahim, M., Harras, K. A., & Youssef, M. (2015). Toward dynamic real-time geo-location databases for TV white spaces. IEEE Network, 29(5), 76–82.
Peng, F., Wang, N., Gao, Y., Cuthbert, L., & Zhang, X. (2013). Geo-location database based TV white space for interference mitigation in LTE femtocell networks. In World of Wireless, Mobile and Multimedia Networks (WoWMoM), 2013 IEEE 14th international symposium and workshops on a, pp. 1–6. IEEE.
Bhushan, N., Li, J., Malladi, D., Gilmore, R., Brenner, D., Damnjanovic, A., et al. (2014). Network densification: The dominant theme for wireless evolution into 5G. IEEE Communications Magazine, 52(2), 82–89.
Andrews, J. G., Baccelli, F., & Ganti, R. K. (2011). A tractable approach to coverage and rate in cellular networks. IEEE Transactions on Communications, 59(11), 3122–3134.
Dhillon, H. S., Ganti, R. K., Baccelli, F., & Andrews, J. G. (2012). Modeling and analysis of k-tier downlink heterogeneous cellular networks. IEEE Journal on Selected Areas in Communications, 30(3), 550–560.
Andrews, J. G. (2013). Seven ways that hetnets are a cellular paradigm shift. IEEE Communications Magazine, 51(3), 136–144.
Chu, X., Lopez-Perez, D., Yang, Y., & Gunnarsson, F. (2013). Heterogeneous cellular networks theory, simulation and deployment (1st ed.). Cambridge: Cambridge University Press.
ElSawy, H., & Hossain, E. (2014). Two-tier hetnets with cognitive femtocells: Downlink performance modeling and analysis in a multichannel environment. IEEE Transactions on Mobile Computing, 13(3), 649–663.
Li, P., Guo, S., Zhuang, W., & Ye, B. (2014). On efficient resource allocation for cognitive and cooperative communications. IEEE Journal on Selected Areas in Communications, 32(2), 264–273.
Huang, K., Lau, V. K. N., & Chen, Y. (2009). Spectrum sharing between cellular and mobile ad hoc networks: Transmission-capacity trade-off. IEEE Journal on Selected Areas in Comm., 27(7), 1256–1267.
Gür, G., Bayhan, S., & Alagöz, F. (2013). Energy efficiency impact of cognitive femtocells in heterogeneous wireless networks. In Proceedings of the 1st ACM workshop on cognitive radio architectures for broadband, pp. 53–60. ACM.
Wang, D., Zou, J., Xiong, H., & Chen, C. W. (2013). Optimal power allocation for hybrid overlay/underlay spectrum sharing in multiband cognitive radio networks. IEEE Transactions on Vehicular Technology, 62, 1827–1837.
Peng, H., & Fujii, T. (2013). Hybrid overlay/underlay resource allocation for cognitive radio networks in user mobility environment. In IEEE 78th vehicular technology conference (VTC Fall), 2013, pp. 1–6. IEEE.
Haider, F., Wang, C.-X., Haas, H., Hepsaydir, E., Ge, X., & Yuan, D. (2015). Spectral and energy efficiency analysis for cognitive radio networks. IEEE Transactions on Wireless Communications, 14(6), 2969–2980.
Luo, Y., Gao, L., & Huang, J. (2013). White space ecosystem: A secondary network operator’s perspective. In Global communications conference (GLOBECOM), 2013 IEEE, pp. 925–930. IEEE.
Um, J., Park, J., Chun, J., Park, S. (2015). Location-probability-based transmission strategy for white space devices with multiple antennas in TV white space. IEEE Transactions on Vehicular Technology, pp. (99), 1–1.
Petrini, V., & Karimi, H. R. (2012). TV white space databases: Algorithms for the calculation of maximum permitted radiated power levels. In Dynamic spectrum access networks (DYSPAN), 2012 IEEE international symposium on, pp. 552–560. IEEE.
Choi, Y.-J., & Shin, K. G. (2011). Opportunistic access of TV spectrum using cognitive-radio-enabled cellular networks. IEEE Transactions on Vehicular Technology, 60(8), 3853–3864.
Tao, X., Zhao, Z., Zhang, H. (2013). Location information based interference control for cognitive radio network in TV white spaces. In IEEE wireless communications and networking conference (WCNC), 2013, pp. 3614–3619. IEEE.
Heath, R. W., Kountouris, M., & Bai, T. (2013). Modeling heterogeneous network interference using poisson point processes. IEEE Transactions on Signal Processing, 61(16), 4114–4126.
Kostić, I. M. (2005). Analytical approach to performance analysis for channel subject to shadowing and fading. IEE Proceedings-Communications, 152(6), 821–827.
Mishra, M. K., & Trivedi, A. (2015). Performance analysis of two tier cognitive heterogeneous cellular network. In Twenty first National Conference on Communications (NCC) 2015, pp. 1–6. IEEE.
Haenggi, M., & Ganti, R. K. (2009). Interference in large wireless networks. Now Publishers Inc.
Li, L., Zhou, X., Xu, H., Li, G. Y., Wang, D., & Soong, A. (2010). Energy-efficient transmission in cognitive radio networks. In 7th IEEE consumer communications and networking conference (CCNC), 2010, pp. 1–5.
Schwartz, S. C., & Yeh, Y.-S. (1982). On the distribution function and moments of power sums with log-normal components. Bell System Technical Journal, 61(7), 1441–1462.
Shen, W., & Zeng, Q.-A. (2008). Cost-function-based network selection strategy in integrated wireless and mobile networks. IEEE Transactions on Vehicular Technology, 57(6), 3778–3788.
Lee, C.-H., & Shih, C.-Y. (2014). Coverage analysis of cognitive femtocell networks. IEEE Wireless Communications Letters, 3(2), 177–180.
Soh, Y. S., Quek, T. Q. S., Kountouris, M., & Shin, H. (2013). Energy efficient heterogeneous cellular networks. IEEE Journal on Selected Areas in Communications, 31(5), 840–850.
Zhang, Q. T. (1996). Outage probability in cellular mobile radio due to nakagami signal and interferers with arbitrary parameters. IEEE Transactions on Vehicular Technology, 45(2), 364–372.
Gil-Pelaez, J. (1951). Note on the inversion theorem. Biometrika, 38(3–4), 481–482.
Zhang, Q. T. (1998). Outage analysis of cellular systems in an arbitrary lognormal shadowed rician environment. In The ninth IEEE international symposium on personal, indoor and mobile radio communication, 1998., vol. 3, pp. 1136–1140.
Jo, H.-S., Sang, Y. J., Xia, P., & Andrews, J. G. (2012). Heterogeneous cellular networks with flexible cell association: A comprehensive downlink sinr analysis. IEEE Transactions on Wireless Communications, 11(10), 3484–3495.
Hasan, Z., Boostanimehr, H., & Bhargava, V. K. (2011). Green cellular networks: A survey, some research issues and challenges. IEEE Communications Surveys & Tutorials, 13(4), 524–540.
De Domenico, A., Calvanese Strinati, E., & Capone, A. (2014). Enabling green cellular networks: A survey and outlook. Computer Communications, 37, 5–24.
Almesaeed, R., Doufexi, A., Dahnoun, N., & Nix, A. R. (Sept 2013). TVWS extension of the 3GPP/ITU channel model. In 2013 IEEE 24th annual international symposium on personal, indoor, and mobile radio communications (PIMRC), pp. 36–40.
Renzo, M. D., Guidotti, A., & Corazza, G. E. (2013). Average rate of downlink heterogeneous cellular networks over generalized fading channels: A stochastic geometry approach. IEEE Transactions on Communications, 61(7), 3050–3071.
Madhusudhanan, P., Restrepo, J. G., Liu, Y., & Brown, T. X. (2012). Downlink coverage analysis in a heterogeneous cellular network. In Global communications conference (GLOBECOM), 2012 IEEE, pp. 4170–4175.
Wolfram mathematica 9.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proof of Theorem 1
When both the tiers (MBS and CFBS tier) use the same channel, it introduces cross tier and co-tier interference in the network. Let total interference is given by I = \(I_{mbs-mbs}+I_{cfbs-mbs}\), where \(I_{mbs-mbs}\) is co-tier interference and \(I_{cfbs-mbs}\) is cross-tier interference for MBS network. If \(I_{mbs-mbs}\) and \(I_{cfbs-mbs}\) are independent, then the CHF of the total interference I can be written as \(\psi _I(\gamma y)\) = \(\psi _{I_{mbs-mbs}(\gamma y)}\cdot \psi _{I_{cfbs-mbs}(\gamma y)}.\) The CHF of I is given by [31]
where \(\mathbb {E} [g^{2/\epsilon }]\) for the Gamma distribution is derived as
By substituting the value of \(\mathbb {E} [g^{2/\epsilon }]\) from (54), (55) can be expressed as
where \({\mathfrak {B}}_{\mathfrak {mc}}=\frac{\pi \gamma ^{2/\epsilon }\left( \xi _{cfbs} \eta _{cfbs}^{2/\epsilon }+\xi _{{mbs}} \eta _{{mbs}}^{2/\epsilon } \right) \vartheta _q ^{2/\epsilon } \varGamma \left( 1-\frac{2}{\epsilon }\right) \varGamma \left( \alpha _q+\frac{2}{\epsilon }\right) }{\varGamma (\alpha _q )}.\)
CHF of the Gamma distribution is given by
So, using (56) and (57), \(\psi (y)\) can be expressed as
The imaginary part of the (58) can be written as [46]
From (19), (59) can be expressed as
So, outage probability of MBS tier is given by
To obtain the exact finite range integral expression, we substitute \(y = \tan (x)\) in (62). Thus, (62) can be written as
which can be simplified as
where \(\gamma = T_m/\eta _{mbs} d_{mbs}^{-\epsilon } .\) \(T_m\) is the SIR threshold for MBS tier.
Appendix 2: Proof of Lemma 1
Let co-tier interference is denoted by \(I_{mbs-mbs}\) for MBS tier. Hence, the CHF of the total interference I is expressed by
where
The outage probability of MBS tier with co-tier interference \({\mathcal {P}}_{\mathrm {mo}}^{mbs}\) is similar to \({\mathcal {P}}_{\mathrm {mc}}^{mbs}.\) So using (63), \({\mathcal {P}}_{\mathrm {mo}}^{mbs}\) is given by
where \(\gamma = T_m/\eta _{mbs} d_{mbs}^{-\epsilon } .\) \(T_m\) is the SIR threshold for the MBS tier.
Appendix 3: Proof of Lemma 2
When CFBS tier works in USST, it introduces co-tier and cross tier interference in the network. Thus, total interference can be expressed by I = \(I_{cfbs-cfbs}\)+\(I_{mbs-cfbs}\), where \(I_{cfbs-cfbs}\) is co-tier interference and \(I_{mbs-cfbs}\) is cross-tier interference for CFBS network [30]. The CHF of the total interference I is similar to the (56). The outage probability of CFBS tier under USST \({\mathcal {P}}_{\mathrm {UL}}^{cfbs}\) is similar to \({\mathcal {P}}_{\mathrm {mc}}^{mbs}\) and it is given by
where \({\mathfrak {B}}_{\mathfrak {ul}}=\frac{\pi \gamma ^{2/\epsilon }\left( \xi _{cfbs} \eta _{cfbs}^{2/\epsilon }+\xi _{{mbs}} \eta _{{mbs}}^{2/\epsilon } \right) \vartheta _q ^{2/\epsilon } \varGamma \left( 1-\frac{2}{\epsilon }\right) \varGamma \left( \alpha _q +\frac{2}{\epsilon }\right) }{\varGamma (\alpha _q )}\) and \(\gamma = T_c/\eta _{cfbs} d_{cfbs}^{-\epsilon } .\) \(T_c\) is the SIR threshold for CFBS tier.
Appendix 4: Proof of Lemma 3
In OTMSST, co-tier interference and interference from TV transmitters are considered to derive the outage probability. Let \(I_{cfbs-cfbs}\) denotes co-tier interference and interference from TV transmitters is expressed by \(I_{tv-cfbs}.\) So, total interference is given by \(I = I_{cfbs-cfbs}+I_{tv-cfbs}.\) The derivation of \({\mathcal {P}}_{\mathrm {ot}}^{cfbs}\) is similar to \({\mathcal {P}}_{\mathrm {mc}}^{mbs}\) and it is given by
and in this case \(\gamma\) is given by \(T_c/\eta _{cfbs}^{tv} d_{cfbs}^{-\epsilon _{tv}} (h_t^{cfbs}h_r^{cfbs})^2.\) \(\xi _{{tv}}\) and \(\eta _{{tv}}\) denote the density and transmitted power of TV transmitter.
Appendix 5: Proof of Theorem 2
From (19) and (36) AER for MBS tier with co-tier and cross tier interference can be written as
where \(\psi (y)=\frac{e^{-y^{2/\epsilon }w^{2/\epsilon } {\mathfrak {B}_{\mathfrak {mc}}^{{\mathfrak {R}}}}e^{-i\pi /\epsilon }}}{(1+i\vartheta _q y)^{\alpha _q}}.\)
By substituting \(-ln(1+w)=\tan (v)\) in (66), we have \(w=e^{-\tan (v)}-1.\) Thus, (66) can be written as
where \(\psi (y)=\frac{e^{-y^{2/\epsilon }(e^{-\tan (v)}-1)^{2/\epsilon } {\mathfrak {B}_{\mathfrak {mc}}^{{\mathfrak {R}}}}e^{-i\pi /\epsilon }}}{(1+i\vartheta _q y)^{\alpha _q}}.\)
Similar to outage analysis and using [46], (67) can be expressed as
To obtain the exact finite range integral expression, we substitute \(y = \tan (x)\) in (68).
Thus, after simplification it can be written as
where \(\mathcal {A}=\tan (x)^{2/\epsilon }e^{-\frac{2 \tan (v)}{\epsilon }} \left( e^{\tan (v)}-1\right) ^{2/\epsilon }\), \(\mathcal {C}=\tan (v)\sec ^2(v)e^{-\tan (v)}.\)
Rights and permissions
About this article
Cite this article
Mishra, M.K., Trivedi, A. & Pattanaik, K.K. Outage and energy efficiency analysis for cognitive based heterogeneous cellular networks. Wireless Netw 24, 847–865 (2018). https://doi.org/10.1007/s11276-016-1371-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-016-1371-3