Abstract
In this paper, we investigate the shaping pulse of faster-than-Nyquist (FTN) signaling by making use of the reduced complexity truncated optimal maximum-likelihood sequence detection. Specifically, the nonorthogonal Gaussian shaping pulse which owns the approximate optimal energy concentration in time-frequency domains is exploited. Moreover, for fair of comparisons, a general benchmark for different shaping pulses is adopted, and based on which, the Euclidean distance (or Mazo limit) and practical information rate performance of FTN signaling with Gaussian pulse and conventional T-orthogonal shaping pulses such as \({\mathrm{sinc}}\) pulse and root raised cosine pulse are evaluated. Theoretical analyses and numerical results demonstrate that when employed with truncated optimal detector and small channel memory at the receiver, the Gaussian pulse could achieve better BER and information rate performance than conventional T-orthogonal pulses.









Similar content being viewed by others
Notes
It should be noted the Ungerboeck model has the equivalent BER performance as that of the Forney model only for un-truncated channel memory. However, since we mainly interested in the practical performance under given detector for different shaping pulses, the difference between Forney and Ungerboeck model with truncated channel memory is beyond the scope of this paper.
For example, when using MLSD (VA or BCJR algorithm), the continuous L ISI taps near the central one g(0) should be considered. However, if the energy of the ISI tap is small enough, it should have been excluded.
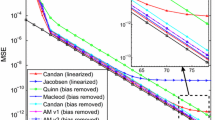
It should be noted that since \(\tau \le 0.7\) beyonds the Mazo limit of root RC and Gaussian pulses and we fix the number of ISI taps considered in the truncated detector, hence, there is a gap between the practical simulation results and the theoretical ISI-free performance bound, and this gap will be enhanced when the packing factor is further reduced.
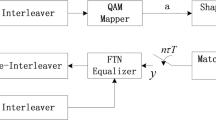
In CS detector, an elaborately designed pre-filter is employed at the receiver, so that the theoretically infinite ISI can be restricted to a short length, in general, \(L = 1\,{\mathrm{or}}\,2\) will be chosen. However, from the information theory perspective, this pre-filter may also result in the loss of the information rate and of course, the BER performance.
References
Anderson, B. J., Rusek, F., & Öwall, V. (2013). Faster-than-Nyquist signaling. Proceeding of IEEE, 101(8), 1817–1830.
Banelli, P., Buzzi, S., Colavolpe, G., et al. (2014). Modulation formats and waveforms for 5G networks: Who will be the heir of OFDM? IEEE Signal Processing Magazine, 31(6), 80–93.
Andrews, J. G., Buzzi, S., Chio, W., & Hanly, V. S. (2014). What will 5G be? IEEE Journal of Selected Areas in Communnications, 32(6), 1065–1082.
Rusek, F., & Anderson, J. B. (2009). Multistream faster than Nyquist signaling. IEEE Transactions on Communnications, 57(5), 1329–1340.
Piemontese, A., Modenini, A., Colavolpe, G., & Alagha, N. S. (2013). Improving the spectral efficiency of nonlinear satellite systems through time-frequnecy packing and advanced receiver processing. IEEE Transactions on Communnications, 61(8), 3404–3412.
Rusek, F., & Prlja, A. (2012). Optimal channel shortening of MIMO and ISI channels. IEEE Transactions on Wireless Communnications, 11(2), 810–818.
Mazo, J. E. (1975). Faster-than-Nyquist signaling. Bell System Technique Journal, 54, 1451–1462.
Liveris, D., & Georghiades, C. N. (2003). Exploiting faster-than-Nyquist signaling. IEEE Transactions on Communnications, 51(9), 1502–1511.
Prlja, A., & Anderson, B. J. (2012). Reduced-complexity receivers for strongly narrowband intersymbol interference introduced by faster-than-Nyqusit signaling. IEEE Transactions on Communnications, 60(9), 2591–2601.
Dasalukunte, D., Rusek, F., & Öwall, V. (2011). Multicarrier faster-than-Nyquist transceivers: Hardware architecture and performance analysis. IEEE Transactions on Circuits and System-I, Regular Papers, 58(4), 827–836.
Abdoli, M., Jia, J. M., & Ma, J. (2014). Turbo-coded single-carrier faster-than-Nyquist transmission. In Proceeding of IEEE International Workshop on Signal Processing and Advances Wireless Communnications (SPAWC) (pp. 170–173).
Anderson, J, B., & Zeinali, M. (2012). Best rate 1/2 convolutional codes for turbo equalization with severe ISI. In Proceeding of IEEE International Symposium on Information Theory (pp. 2366–2370).
Sen, P., Aktas. T., & Yilmaz, A. O. (2014). A low-complexity graph-Based LMMSE Receiver Designed for colored noise induced by FTN-signaling. In Proceeding of IEEE Wireless Communnications and Networking Conference (pp. 642–647).
Sugiura, S. (2013). Frequency-domain equalization of faster-than-Nyquist signaling. IEEE Wireless Communnications Letters, 2(5), 555–558.
Sugirua, S., & Hanzo, L. (2015). Frequency-domain equalization aided iterative detection of faster-than-Nyquist signaling. IEEE Transactions on Vehicular Technology, 64(5), 2122–2128.
Froney, G. D. (1972). Maximum-likelihood sequence estimation of digital sequences in the presence of intersymbol interference. IEEE Transactions on Informaton Theory, 18, 363–378.
Ungerboeck, G. (1974). Adaptive maximum-likelihood receiver for carrier-modulated data transmission systems. IEEE Transactions on Communnications, 22, 624–636.
Rusek, F., Colavolpe, G., & Sundberg, C. W. (2015). 40 years with the Ungerboeck model: A look at its potentialities. Lecture Notes: IEEE Signal Processing Magazine.
Bahl, L. R., Cocke, J., Jelinke, F., & Raviv, R. (1974). Optimal decoding of linear codes for minimizing symbol error rate. IEEE Transactions on Information Theory, 20, 284–287.
Colavolpe, G., & Barbieri, A. (2005). On MAP symbol detection for ISI channels using the Ungerboeck observation model. IEEE Communnications Letters, 9(8), 720–722.
Zhou, J., Li, D., & Wang, X. (2012). Generalized faster-than-Nyquist signaling. In Proceeding of IEEE International Symposium on Information Theory (pp. 1478–1482).
Piemontese, A., Modenini, A., Colavolpe, G., & Alagha, S. N. (2013). Improving the spectral efficiency of nonlinear satellite systems through time-frequency packing and advanced receiver processing. IEEE Transactions on Communnications, 61(8), 3404–3412.
Rusek, F., & Anderson, J. B. (2008). Non-binary and precoded faster than Nyquist signaling. IEEE Transactions on Communications, 56(5), 808–817.
Anderson, B. J., & Rusek, F. (2007). Optimal side lobes under linear and faster-than-Nyquist modulation. In Proceeding of International Symposium on Information Theory (pp. 2301–2304).
Floch, B. L., Alard, M., & Berrou, C. (1995). Coded orthogonal frequency division multiplex. Proceeding of IEEE., 83(6), 982–996.
Siohan, P., & Roche, C. (2000). Cosine-modulated filterbanks based on extended Gaussian functions. IEEE Transactions on Signal Processing, 48(11), 3052–3061.
Le, C., Schellmann, M., & Fuhrwerk, M., et al. (2014). On the practical benefits of faster-than-Nyquist signaling. In Proceeding of International Conference on Advanced Technology Communnications, (pp. 208–213).
Proakis, G, J. (2008). Digital communications (5th ed.). New York: McGraw-Hill.
Strohmer, T., & Beaver, S. (2007). Optimal OFDM design for time-frequency dispersive channels. IEEE Transactions on Communnications, 51(7), 1111–1122.
Han, F., & Zhang, X. (2007). Hexagonal multicarrier modulation: A robust transmission scheme for time-frequency dispersive channels. IEEE Transactions on Signal Processing, 55(5), 1955–1961.
ETSI EN 302 217-2-2: (2014) Fixed radio systems; Characteristics and requirements for point-to-point equipment and antennas; Part 2-2: Digital systems operating in frequency bands where frequency co-ordination is applied; Harmonized EN covering the essential requirements of article 3.2 of the R&TTE directive. Available: http://www.etsi.org.
Rusek, F., & Fertonani, F. (2009). Lower bounds on the information rate of intersymbol interference channels based on the Ungerboeck observation model. In: Proceeding of IEEE international symposium on information theory (pp. 1649–1653). Korea: Seoul.
Modenini, A., Rusek, F., & Colavolpe, G. (2015). Adaptive rate-maximzing channel shortening for ISI channels. IEEE Communnications Letters, 19(12), 2090–2093.
Modenini, A., Rusek, F., & Colavolpe, G. (2013). Optimal transmitter filters for ISI channels under channel shortening detection. IEEE Transactions on Communnications, 61(12), 4997–5005.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No 61671476). The authors also would like express their great gratitude to Prof. Anderson, B, John for his kind reading and many helpful comments and suggestions of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Peng, S., Liu, A., Pan, X. et al. Shaping pulse of faster-than-Nyquist signaling with truncated optimal detector. Wireless Netw 24, 2609–2619 (2018). https://doi.org/10.1007/s11276-017-1491-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-017-1491-4