Abstract
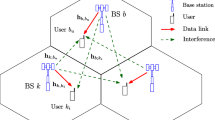
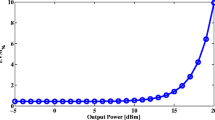
This paper studies the energy efficient joint user scheduling and transmit beamforming in the downlink of a single-cell distributed antenna system. Due to the distributed nature of antenna units, traditional power consumption model cannot be applied without the backhauling power taken into account. Therefore, under the constraints of the minimum rate requirement of each user and the transmit power budget of each distributed antenna unit, we maximize the system energy efficiency through making a tradeoff between the transmitting power and the backhauling power. By employing the parametric equivalence method to deal with the fractional objective and the \(\ell _1\)-norm relaxation method to cope with the user scheduling problem, the energy efficiency maximization is turned into a standard difference of convex program and then solved via the successive convex approximation method. Finally, the optimal sparse transmit beamforming vectors are obtained during the weighting factor iteration process, with the aim of minimizing the total power consumption while maintaining the achieved rate of each user. Extensive simulations are conducted to demonstrate the effectiveness of proposed scheme. Simulation results show that energy efficiency can benefit from not only the user scheduling but also the transmit beamforming optimization.







Similar content being viewed by others
References
Saleh, A. A. M., Rustako, A. J., & Roman, R. S. (1987). Distributed antennas for indoor radio communications. IEEE Transactions on Communications, 35(12), 1245–1251.
Li, H. M., Hajipour, J., Attar, A., & Leung, V. C. M. (2011). Efficient HetNet implementation using broadband wireless access with fiber-connected massively distributed antennas architecture. IEEE Wireless Communications, 18(3), 72–78.
Attar, A., Li, H. M., & Leung, V. C. M. (2011). Green last mile: How fiber-connected massively distributed antenna systems can save energy. IEEE Wireless Communications, 18(5), 66–74.
Hong, X. M., Jie, Y., Wang, C. X., et al. (2013). Energy-spectral efficiency trade-off in virtual MIMO cellular systems. IEEE Journal on Selected Areas in Communications, 31(10), 2128–2140.
Cong, X., Li, G. Y., Zhang, S. Q., et al. (2011). Energy- and spectral-efficiency tradeoff in downlink OFDMA networks. IEEE Transactions on Wireless Communications, 10(11), 3874–3886.
Yang, G. R., Guo, J. L., Liu, G., & Gao, S. S. (2016). A cooperation method of mobile ad hoc network nodes based on energy efficiency. Radio Engineering, 46(5), 5–8.
da Silva, M. Marques, & Monteiro, F. A. (2014). MIMO processing for 4G and beyond: Fundamentals and evolution. Boca Raton: CRC Press Auerbach Publications.
Jiang, D. D., Xu, Z. Z., Li, W. P., Yao, C. P., Lv, Z. H., & Li, T. (2016). An energy-efficient multicast algorithm with maximum network throughput in multi-hop wireless networks. Journal of Communications and Networks, 18(5), 713–724.
Ren, H., Liu, N., & Pan, C. H. (2016). Energy efficient transmission for multicast services in MISO distributed antenna systems. IEEE Communications Letters, 20(4), 756–759.
Kim, H., Li, R. R., Song, C., Lee, K. J., & Lee, I. (2015). Optimal power allocation scheme for energy efficiency maximization in distributed antenna systems. IEEE Transactions on Communications, 63(2), 431–440.
Wang, J., Feng, W., Chen, Y., & Zhou, S. D. (2016). Energy efficient power allocation for multicell distributed antenna systems. IEEE Communications Letters, 29(1), 177–180.
Kim, H., Park, E., Park, H., & Lee, I. (2013). Beamforming and power allocation designs for energy efficiency maximization in MISO distributed antenna systems. IEEE Communications Letters, 17(11), 2100–2103.
He, C. L., Sheng, B., Zhu, P. C., & You, X. H. (2012). Energy efficiency and spectral efficiency tradeoff in downlink distributed antenna systems. IEEE Wireless Communications Letters, 1(3), 153–156.
He, C. L., Sheng, B., Zhu, P. C., You, X. H., & Li, Y. (2013). Energy- and spectral-efficiency tradeoff for distributed antenna systems with proportional fairness. IEEE Journal on Selected Areas in Communications, 31(5), 894–902.
Isheden, C., & Fettweis, G. P. (2010). Energy-efficient multi-carrier link adaptation with sum rate dependent circuit power. In Procedings of IEEE GlobeCom.
Xiao, X., Tao, X. M., & Lu, J. H. (2013). QoS-aware energy-efficient radio resource scheduling in multi-user OFDMA systems. IEEE Communications Letters, 17(1), 75–78.
Ng, D. W. K., Lo, E. S., & Schober, R. (2012). Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas. IEEE Transactions on Wireless Communications, 11(9), 3292–3304.
He, C. L., Li, G. Y., Zheng, F., et al. (2014). Energy-efficient resource allocation in OFDM systems with distributed antennas. IEEE Transactions on Vehicular Technology, 63(3), 1223–1231.
Zhu, H. L., & Wang, J. Z. (2013). Resource allocation in OFDMA-based distributed antenna systems. In Proceedings of IEEE ICCC (pp. 565–570).
Kim, H., Lee, S. R., Lee, K. J., et al. (2012). Transmission schemes based on sum rate analysis in distributed antenna systems. IEEE Transactions on Wireless Communications, 11(3), 1201–1209.
Lei, Z., Ji, Y. S., & Yang, K. (2012). Energy efficient resource allocation in mobile networks with distributed antenna transmission. Mobile Networks and Applications, 17, 36–44.
Joung, J., Chia, Y. K., & Sun, S. Energy-efficient large-scale distributed-antenna system (L-DAS) for multiple users. http://arxiv.org/abs/1312.1870v2.
Arnold, O., Richter, F., & Fettweis, G. et al. (2010). Power consumption modeling of different base station types in heterogeneous cellular networks. In Proceedings future network and mobile summit (pp. 1–8).
Tombaz, S., Monti, P., & Wang, K. et al. (2011). Impact of backhauling power consumption on the deployment of heterogeneous mobile networks. In Proceedings IEEE GLOBECOM (pp. 1–5).
Bjornson, E., Sanguinetti, L., Hoydis, J., & Debbah, M. (2015). Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer? IEEE Transactions on Wireless Communications, 14(6), 3059–3075.
Mohammed, S. (2014). Impact of transceiver power consumption on the energy efficiency of zero-forcing detector in massive MIMO systems. IEEE Transactions on Communications, 62(11), 3874–3890.
Li, C., Zhang, J., & Letaief, K. B. (2014). Throughput and energy efficiency analysis of small cell networks with multi-antenna base stations. IEEE Transactions on Wireless Communications, 13(5), 2505–2517.
Yan, J. L., Wang, Y., Yang, G. R., Guo, Y. T., & Wu, W. (2016). Energy efficient resource allocation in orthogonal frequency division multiple access-based distributed antenna systems. IET Communications, 10(10), 1214–1220.
Matskani, E., Sidiropoulos, N. D., Luo, Z. Q., & Tassiulas, L. (2008). Convex approximation techniques for joint multiuser downlink beamforming and admission control. IEEE Transactions on Wireless Communications, 7(7), 2682–2693.
Derrick, W. K. N., Ernest, S. L., & Robert, S. (2012). Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas. IEEE Transactions on Wireless Communications, 11(9), 3292–3304.
Kha, H. H., Tuan, H. D., & Nguyen, H. H. (2012). Fast global optimal power allocation in wireless networks by local D.C. programming. IEEE Transactions on Wireless Communications, 11(2), 510–515.
Dinkelbach, W. (1967). On nonlinear fractional programming. Management Science, 13, 492–498.
Grant, M., & Boyd, S. (2011). CVX: Matlab software for disciplined convex programming. http://cvxr.com/cvx/. Accessed 18 June 2016.
Luo, Z. Q., Ma, W. K., So, A. M. C., et al. (2010). Semidefinite relaxation of quadratic optimization problems. IEEE Signal Processing Magazine, 27(3), 20–34.
Candes, E. J., Wakin, M. B., & Boyd, S. P. (2008). Enhancing sparsity by reweighted l1 minimization. Journal of Fourier Analysis and Applications, 14(5), 877–905.
Zhao, J., Quek, T. Q. S., & Lei, Z. D. (2013). Coordinated multipoint transmission with limited backhaul data transfer. IEEE Transactions on Wireless Communications, 12(6), 2762–2775.
Ye, Y. (1997). Interior point algorithms: Theory and analysis. Hoboken, NJ: Wiley.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.
Liu, Y. F., Dai, Y. H., & Luo, Z. Q. (2011). Coordinated beamforming for MISO interference channel: Complexity analysis and efficient algorithms. IEEE Transactions on Signal Processing, 59(3), 1142–1157.
Acknowledgements
The study was funded by the Open Foundation of the Science and Technology on Communication Networks Laboratory.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A Proof of Proposition 1
With parameter \(\lambda\) and initialized \(\overline{{\mathbf{W}}}\), let \(\widetilde{\varGamma }_{\lambda }({\mathbf{W}},\overline{{\mathbf{W}}})\) denote the value of (18a) when the beam matrix is \({\mathbf{W}}\), which is shown as below
Since \(g_k({\mathbf{W}})\) is a concave function, we have
At the mth SCA iteration, with initialized \(\overline{{\mathbf{W}}}[m]\), we obtain the optimal objective of problem (18) as follows:
where \(\varGamma _{\lambda }({\mathbf{W}}^*[m])\) is the value of objective function (15a) with the beam matrix \({\mathbf{W}}^*[m]\).
According to the SCA iteration: \(\overline{{\mathbf{W}}}_k[m+1]={\mathbf{W}}_k^*[m]\), we have
Since \({\mathbf{W}}^*[m+1]\) is the optimal solution of problem (18) with initialized \(\overline{{\mathbf{W}}}[m+1]\), we have
Finally, combining (25), (26), and (27), we obtain
For simplicity, let \(\widetilde{\varGamma }_{\lambda }^*[m]=\widetilde{\varGamma }_{\lambda }({\mathbf{W}}^*[m],\overline{{\mathbf{W}}}[m])\). Thus, with the iteration in (19), the optimal objective sequence \(\{\widetilde{\varGamma }_{\lambda }^*[m]\}\) is monotonically increased. Moreover, due to the power constraint of each DAU, \(\widetilde{\varGamma }^*_{\lambda }[m]\) is always upper-bounded. Then, we have proved the convergence of the SCA iteration. Furthermore, since the original objective function in (15a) is neither convex nor concave, the convex approximation based on the first-order Taylor series approximation and the SCA iteration can only obtain a local optimum of problem (15).
Appendix B Proof of Proposition 2
The Lagrangian of the problem (18) is
where \(\mathbf{\alpha }=[\alpha _1,\ldots ,\alpha _K]^T\) and \(\mathbf{\beta }=[\beta _1,\ldots ,\beta _N]^T\) are the dual vectors for the SINR constraints and the power restrictions, respectively. \({\mathbf{Z}}_k\) is an additional slack matrix.
The partial derivative of \({\mathcal {L}}({\mathbf{W}},\mathbf{\alpha },\mathbf{\beta })\) over \({\mathbf{W}}_i\) is
Substituting (31) and (32) into (30),
According to the KKT conditions [38], we have
where \({\mathbf{W}}_i^{\star }\) and \({\mathbf{Z}}_i^{\star }\) are the converged optimal solution of problem (18) after the SCA iteration. Moreover, due to the convergence of the SCA iteration, we can approximate \({\mathbf{W}}_k^{\star }=\overline{{\mathbf{W}}}_k\), \(\forall k\). Then, from (34), we deduce that \({\mathbf{Z}}_i^{\star }={\mathbf{S}}_i^{\star }-{\mathbf{V}}_i^{\star }\), where
It can be observed that, if \(1-\frac{\lambda P_{bh}}{C_{bh}}\text{Tr}({\mathbf{W}}_k^{\star })\ge 0 \ (\forall k)\), then the first part of \({\mathbf{S}}_i^{\star }\) is semi-definite. Moreover, since the Lagrangian multipliers are non-negative values, we know that \({\mathbf{S}}_i^{\star }\) is a definite matrix with a rank of \(\sum _{n=1}^{N}M_n\). Also, the first part of \({\mathbf{V}}_i^{\star }\) is semi-definite, and \({\mathbf{V}}_i^{\star }\) is a matrix with rank one. According to (35), we know that \(\text{rank}({\mathbf{W}}_i^{\star })\le \sum _{n=1}^{N}M_n-\text{rank}({\mathbf{Z}}_i^{\star })\). Since \(\text{rank}({\mathbf{Z}}_i^{\star })\ge \text{rank}({\mathbf{S}}_i^{\star })-\text{rank}({\mathbf{V}}_i^{\star })\), we obtain \(\text{rank}({\mathbf{W}}_i^{\star })\le 1\), \(\forall i\). Obviously, \(\text{rank}({\mathbf{W}}_i^{\star })=0\) is not the optimal solution of problem (15). Finally, one can deduce that if for any user \(k=1,\ldots ,K\), there exists \(1-\frac{\lambda P_{bh}}{C_{bh}}\text{Tr}({\mathbf{W}}_k^{\star })\ge 0\), then \(\text{rank}({\mathbf{W}}_k^{\star })=1\).
Rights and permissions
About this article
Cite this article
Wang, Y., Yan, J., Li, D. et al. Energy efficient joint user scheduling and transmit beamforming in downlink DAS. Wireless Netw 25, 3223–3237 (2019). https://doi.org/10.1007/s11276-018-1714-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-018-1714-3