Joint optimization of channel allocation and power control for cognitive radio networks with multiple constraints

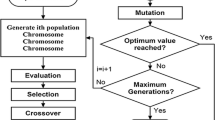
Abstract

With the increasing demands for wireless communication, efficiently using the spectrum resource has always been an important research topic. In this paper, the problem of N pairs of Secondary Users (SU) sharing K available channels with M Primary Users and its associated problem of optimal channel allocation and power control are studied. To investigate a joint channel and power allocation for the underlay-based Cognitive Radio Networks, a sum-rate maximization problem of the SU with consideration of Quality of Service and the constraints of interference temperature and outage probability is formulated as a Mixed Integer Nonlinear Programming problem. To solve it, the objective function is divided into two sub-optimization problems: channel allocation and power control. First of all, we propose to use the Genetic Algorithm Channel Allocation algorithm (GACA) to solve the channel allocation optimization problem and get the optimal channel allocation strategy. The power control optimization is then followed, but the problem is a fractional form of function with coupling constraints that is non-convex and cannot be solved directly with convex optimization. To this end, when the SINR is sufficiently high, we obtain optimal power control strategy by introducing Geometric Programming and auxiliary variables to convert non-convex to Convex Geometric Programming. When SINR is the medium to low value, we use an iterative algorithm known as the Single Condensation Method to solve it. Finally, through our proposed iterative algorithm, that is, Joint Optimization Algorithm (JOA), the optimal solution is obtained. Moreover, the convergence and complexity of the algorithm are analyzed. The time complexity of JOA in the worst case is $O(N^{3} \sqrt N )$. In order to show the generality of the channel state, in the simulation part, we design a perfect CSI optimal solution scenario and a imperfect CSI sub-optimal solution scenario. Simulation results show that the proposed algorithm can achieve better performance under different CSI states.

Appendix A

1.1 Proof of CGP (32)

We let $\tilde{T}_{l} = c_{l} e^{{o_{l}^{T} \tilde{p}}},$ denoted as o_l = (o_1l, o_2l, …, o_nl)^T. Meanwhile, let $\nabla \tilde{T}_{l} = \tilde{T}_{l} o_{l},$ denoted as $\tilde{f}(\tilde{p}) = \log \tilde{f}_{0} (\tilde{p}),$ then $\nabla \tilde{f}(\tilde{p}) = {{\nabla \tilde{f}_{0} (\tilde{p})} \mathord{\left/ {\vphantom {{\nabla \tilde{f}_{0} (\tilde{p})} {\tilde{f}_{0} (\tilde{p})}}} \right. \kern-0pt} {\tilde{f}_{0} (\tilde{p})}},$

$$\begin{aligned} \nabla^{2} \tilde{f}(\tilde{p}) = & \frac{{\tilde{f}_{0} (\tilde{p})\nabla^{2} \tilde{f}_{0} (\tilde{p}) - \nabla \tilde{f}_{0} (\tilde{p})\nabla \tilde{f}_{0} (\tilde{p})^{T} }}{{\left[ {\tilde{f}_{0} (\tilde{p})} \right]^{2} }} \\ = & \frac{{\left( {\sum\limits_{{l \in L_{0} }} {\tilde{T}_{l} } } \right)\left( {\sum\limits_{{l \in L_{0} }} {\tilde{T}_{l} o_{l} o_{l}^{T} } } \right) - \left( {\sum\limits_{{l \in L_{0} }} {\tilde{T}_{l} o_{l} } } \right)\left( {\sum\limits_{{l \in L_{0} }} {\tilde{T}_{l} o_{l}^{T} } } \right)}}{{\left[ {\tilde{f}_{0} (\tilde{p})} \right]^{2} }} \\ \end{aligned}$$

where

$$\begin{aligned} & \sum\limits_{{l \in L_{0} }} {\sum\limits_{{l^{\prime} \in L_{0} }} {\tilde{T}_{l} \tilde{T}_{{l^{\prime}}} o_{l} o_{l}^{T} } } - \sum\limits_{{l \in L_{0} }} {\sum\limits_{{l^{\prime} \in L_{0} }} {\tilde{T}_{l} \tilde{T}_{{l^{\prime}}} o_{l} o_{{l^{\prime}}}^{T} } } \\ & \quad = \sum\limits_{{l < l^{\prime}}} {\sum\limits_{{l^{\prime} \in L_{0} }} {\tilde{T}_{l} \tilde{T}_{{l^{\prime}}} \left( {o_{l} o_{l}^{T} + o_{{l^{\prime}}} o_{{l^{\prime}}}^{T} } \right) - } } \sum\limits_{{l < l^{\prime}}} {\sum\limits_{{l^{\prime} \in L_{0} }} {\tilde{T}_{l} \tilde{T}_{{l^{\prime}}} \left( {o_{l} o_{{l^{\prime}}}^{T} + o_{{l^{\prime}}} o_{l}^{T} } \right)} } \\ & \quad = \sum\limits_{{l < l^{\prime}}} {\sum\limits_{{l^{\prime} \in L_{0} }} {\tilde{T}_{l} \tilde{T}_{{l^{\prime}}} \left( {o_{l} - o_{{l^{\prime}}} } \right)} } \left( {o_{l} - o_{{l^{\prime}}} } \right)^{T} \\ \end{aligned}$$

Du to $\tilde{T}_{l} > 0,\tilde{T}_{{l^{\prime}}} > 0,$ and $\left( {o_{l} - o_{{l^{\prime}}} } \right)\left( {o_{l} - o_{{l^{\prime}}} } \right)^{T}$ is positive definite. Therefore, $\log \tilde{f}_{0} (\tilde{p})$ is a convex function. Similarly, we can prove that $\log \tilde{f}_{i} (\tilde{p}),\;i = 1,2, \ldots ,N$ is a convex function, so that Eq. (31) is a Convex Geometric Programming problem (CGP).