Abstract
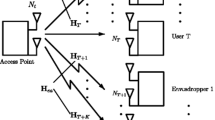
In this paper, we investigate the secure downlink transmission in a multi-user massive multiple-input multiple-output system assuming there is a passive multi-antenna eavesdropper (Eve) that intends to intercept information of a target user. Specifically, we employ the distributed massive antenna sets at the base station, which are known as remote radio heads (RRHs). With cooperative maximum-ratio transmission beamforming, artificial noise (AN) generation and autonomous power allocation at each RRH, the closed-form deterministic lower bound of the ergodic secrecy rate is derived by random matrix theory. Based on a simplified channel model, the impacts of various parameters on secrecy performance, such as uplink training energy, eavesdropper’s antennas number, power allocation factor, have been analyzed in detail, which provide intuitive insights for optimization and performance evaluation. Moreover, by exploiting complementary geometric programming, an power optimization algorithm over signal and AN power is derived subject to total power and Eve’s signal-to-interference-plus-noise ratio constraints. Numerical results have been presented to reveal the system’s secrecy performance and confirm all analysis results in this paper.







Similar content being viewed by others
References
Marzetta, T. L. (2015). Massive MIMO: An introduction. Bell Labs Technical Journal, 20, 11–22.
Bjornson, E., Larsson, E. G., & Marzetta, T. L. (2016). Massive MIMO: Ten myths and one critical question. IEEE Communications Magazine, 54(2), 114–123.
Abdo, A. M. A., Zhao, X., Zhang, R., Zhou, Z., Zhang, J., Zhang, Y., et al. (2018). MU-MIMO downlink capacity analysis and optimum code weight vector design for 5G big data massive antenna millimeter wave communication. Wireless Communications and Mobile Computing, 2018, 1–12.
Zhao, X., Abdo, A. M. A., Xu, C., Geng, S., Zhang, J., & Memon, I. (2018). Dimension reduction of channel correlation matrix using CUR-decomposition technique for 3-D massive antenna system. IEEE Access, 6, 3031–3039.
Kamga, G. N., Xia, M., & Aissa, S. (2016). Spectral-efficiency analysis of massive MIMO systems in centralized and distributed schemes. IEEE Transactions on Communications, 64(5), 1930–1941.
Heath, R. W., Wu, T., Kwon, Y., & Soong, A. C. K. (2011). Multiuser MIMO in distributed antenna systems with out-of-cell interference. IEEE Transactions on Signal Processing, 59(10), 4885–4899.
Zhang, J., Wen, C. K., Jin, S., Gao, X., & Wong, K. K. (2013). On capacity of large-scale MIMO multiple access channels with distributed sets of correlated antennas. IEEE Journal on Selected Areas in Communications, 31(2), 133–148.
Li, J., Wang, D., Zhu, P., Wang, J., & You, X. (2018). Downlink spectral efficiency of distributed massive MIMO systems with linear beamforming under pilot contamination. IEEE Transactions on Vehicular Technology, 67(2), 1130–1145.
Yang, A., Jing, Y., Xing, C., Fei, Z., & Kuang, J. (2015). Performance analysis and location optimization for massive MIMO systems with circularly distributed antennas. IEEE Transactions on Wireless Communications, 14(10), 5659–5671.
He, C., Yin, J., He, Y., Huang, M., & Zhao, B. (2016). Energy efficiency of distributed massive MIMO systems. Journal of Communications and Networks, 18(4), 649–657.
Li, J., Wang, D., Zhu, P., & You, X. (2017). Uplink spectral efficiency analysis of distributed massive MIMO with channel impairments. IEEE Access, 5, 5020–5030.
Truong, K. T., & Heath, R. W. (2013). The viability of distributed antennas for massive MIMO systems. In Proceeding of 2013 Asilomar conference on signals, systems and computers (pp. 1318–1323).
Memon, I., Arain, Q. A., Memon, M. H., Mangi, F. A., & Akhtar, R. (2017). Search me if you can: Multiple mix zones with location privacy protection for mapping services. International Journal of Communication Systems, 30(16), e3312.
Memon, I., Ali, Q., Zubedi, A., & Mangi, F. A. (2017). DPMM: Dynamic pseudonym-based multiple mix-zones generation for mobile traveler. Multimedia Tools and Applications, 76(22), 24359–24388.
Zhao, N., Yu, F. R., Sun, H., & Li, M. (2016). Adaptive power allocation schemes for spectrum sharing in interference-alignment-based cognitive radio networks. IEEE Transactions on Vehicular Technology, 65(5), 3700–3714.
Cao, Y., Zhao, N., Yu, F. R., Jin, M., Chen, Y., Tang, J., et al. (2018). Optimization or alignment: Secure primary transmission assisted by secondary networks. IEEE Journal on Selected Areas in Communications, 36(4), 905–917.
Le, T. A., Vien, Q. T., Nguyen, H. X., Ng, D. W. K., & Schober, R. (2017). Robust chance-constrained optimization for power-efficient and secure SWIPT systems. IEEE Transactions on Green Communications and Networking, 1(3), 333–346.
Zhou, F., Li, Z., Cheng, J., Li, Q., & Si, J. (2017). Robust AN-aided beamforming and power splitting design for secure MISO cognitive radio with SWIPT. IEEE Transactions on Wireless Communications, 16(4), 2450–2464.
Le, T. A., Nguyen, H. X., Vien, Q. T., & Karamanoglu, M. (2015). Secure information transmission and power transfer in cellular networks. IEEE Communications Letters, 19(9), 1532–1535.
Kapetanovic, D., Zheng, G., & Rusek, F. (2015). Physical layer security for massive MIMO: An overview on passive eavesdropping and active attacks. IEEE Communications Magazine, 53(6), 21–27.
Al-nahari, A. (2016). Physical layer security using massive multiple-input and multiple-output: Passive and active eavesdroppers. IET Communications, 10(1), 50–56.
Wu, Y., Schober, R., Ng, D. W. K., Xiao, C., & Caire, G. (2016). Secure massive MIMO transmission with an active eavesdropper. IEEE Transactions on Information Theory, 62(7), 3880–3900.
Zhu, J., Schober, R., & Bhargava, V. K. (2016). Linear precoding of data and artificial noise in secure massive MIMO systems. IEEE Transactions on Wireless Communications, 15(3), 2245–2261.
Zhu, J., Schober, R., & Bhargava, V. K. (2014). Secure transmission in multicell massive MIMO systems. IEEE Transactions on Wireless Communications, 13(9), 4766–4781.
Liu, C., & Malaney, R. (2016). Location-based beamforming and physical layer security in Rician wiretap channels. IEEE Transactions on Wireless Communications, 15(11), 7847–7857.
Chen, B., Zhu, C., Shu, L., Su, M., Wei, J., Leung, V. C., et al. (2016). Securing uplink transmission for lightweight single-antenna UEs in the presence of a massive MIMO eavesdropper. IEEE Access, 4, 5374–5384.
Chen, B., Zhu, C., Li, W., Wei, J., Leung, V. C., & Yang, L. T. (2016). Original symbol phase rotated secure transmission against powerful massive MIMO eavesdropper. IEEE Access, 4, 3016–3025.
Guo, K., Guo, Y., & Ascheid, G. (2016). Security-constrained power allocation in MU-massive-MIMO with distributed antennas. IEEE Transactions on Wireless Communications, 15(12), 8139–8153.
Guo, K., Guo, Y., & Ascheid, G. (2015). Distributed antennas aided secure communication in MU-massive-MIMO with QoS guarantee. In Proceeding of 2015 IEEE 82nd vehicular technology conference (pp. 1–7).
Hasan, M. K., Ismail, A. F., Islam, S., Hashim, W., Ahmed, M. M., & Memon, I. (2018). A novel HGBBDSA-CTI approach for subcarrier allocation in heterogeneous network. Telecommunication Systems. https://doi.org/10.1007/s11235-018-0473-x.
Peng, S., Liu, A., Song, L., Memon, I., & Wang, H. (2018). Spectral efficiency maximization for deliberate clipping-based multicarrier faster-than-Nyquist signaling. IEEE Access, 6, 13617–13623.
Hoydis, J., Brink, S., & Debbah, M. (2013). Massive MIMO in the UL/DL of cellular networks: How many antennas do we need? IEEE Journal on Selected Areas in Communications, 31(2), 160–171.
Bjornson, E., Hoydis, J., Kountouris, M., & Debbah, M. (2014). Massive MIMO systems with non-ideal hardware: Energy efficiency, estimation, and capacity limits. IEEE Transactions on Information Theory, 60(11), 7112–7139.
Jose, J., Ashikhmin, A., Marzetta, T. L., & Vishwanath, S. (2011). Pilot contamination and precoding in multi-cell TDD systems. IEEE Transactions on Wireless Communications, 10(8), 2640–2651.
Tulino, A. M., & Verdu, S. (2004). Random matrix theory and wireless communications. Foundations and Trends in Communications and Information Theory, 1(1), 1–182.
Avriel, M., & Williams, A. C. (1970). Complementary geometric programming. SIAM Journal on Applied Mathematics, 19(1), 125–141.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.
Acknowledgements
Funding was provided by the Jiangsu Provincial Natural Science Foundation of China (Grant No. BK20141069).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
According to the statistic characteristics of the MMSE channel estimate and estimation error, exploiting random matrix theory, the intended signal, multi-user interference, and AN leakage can be rewritten as
The above statistics can be easily obtained by the law of large numbers and central limit theorem with infinite BS antenna number \({N_T} \rightarrow \infty \). Furthermore, we can easily get that
Then we focus on the variance term, i.e.
Obviously, the last two terms at far right of the above equation can be obtained easily by (40) and (41). Meanwhile, the first component can be unfolded as
It is recalled that channels from different RRHs are mutually independent. Also it is noted that \({\left\| {{{\hat{\mathbf{g}}}_{mk}}} \right\| ^2} \sim {{\mathcal{W}}_1}\left( {{N_T},{\phi _{mk}}} \right) \) follows Wishart distribution. Based on the expectation properties of Wishart matrix [35], we can get that \({{\mathbb {E}}}\left[ {{{\left\| {{{\hat{\mathbf{g}}}_{mk}}} \right\| }^4}} \right] = {\left( {{\mathrm{tr}}\left( {{{{\varvec{\Psi }}} _{mk}}} \right) } \right) ^2} + {\mathrm{tr}}\left( {{{\varvec{\Psi }}} _{mk}^2} \right) \), thus
Hence, we can finally obtain the variance term as
Inserting these results into (11), we can yield the expression as (13), which concludes the proof.
Appendix 2
According to the assumption, all UTs are located uniformly in the region. So we can easily consider that there are \(\frac{K}{M}\) UTs in the major service region of each RRH. Based on these conditions and assumptions, the intended signal, multi-user interference, and AN leakage in (13) can be rewritten as
Recalling (13), we can simply SINR of kth UT as
Similarly, we can also obtain the SINR of Eve as
Plugging these SINR expressions of potential UT and Eve into (25) and (26), we finally achieve ergodic secrecy rate of kth UT as (27). This completes the proof.
Appendix 3
According to definition in [36], we know that one set with \(\left\{ {\left. x \right| {g_1}\left( x \right) \le 0, \ldots ,} \right. \left. {{g_K}\left( x \right) \le 0} \right\} \) is regular when: (1) this set is nonempty and compact; (2) For any \({x^*}\) with a nonempty index set \({\mathcal{K} }= \left\{ {\left. k \right| {g_k}\left( {x'} \right) = 0} \right\} \), the convex hull of \(\nabla {g_k}\left( {{x^*}} \right) ,k \in {\mathcal{K}}\) doesn’t contain the origin. For problem \({J_2}\), we similarly define an index set \({\mathcal{K}} = {{\mathcal{K}}_P} \cup {{\mathcal{K}}_{UT}} \cup {{\mathcal{K}}_E}\), where \({{\mathcal{K}}_P} = \left\{ {\left. p \right| {g_{P,p}} = 0} \right\} , {{\mathcal{K}}_U} = \left\{ {\left. u \right| {g_{U,u}} = 0} \right\} \) and \({{\mathcal{K}}_E} = \left\{ {\left. e \right| {g_{E,e}} = 0} \right\} \) with \({g_{P,p}}, {g_{U,u}}, {g_{E,e}}\) representing the constraints of total power, UT’s and Eve’s SINR. As there are \(M + 2\) variables in these equations, so we know that \(\left| {\mathcal{K}} \right| \le M + 2\) always holds true. As the feasible set of \({J_2}\) is not empty and compact, we only need prove that the origin does not lie in the convex hull of \(\nabla {g_{P,p}} , p \in {{\mathcal{K}}_P},\nabla {g_{U,u}} , u \in {{\mathcal{K}}_U}\) and \(\nabla {g_{E,e}} , e \in {{\mathcal{K}}_E}\). Note that \(\left| {{{\mathcal{K}}_P}} \right| = 1\). We need to prove that there is not non-negative vector to satisfing the equation \({\mathbf{A}}\theta = {\mathbf{b}}\), where
Obviously, the dimensions of A and b are \(\left( {M + 3} \right) \times \left| {\mathcal{K}} \right| \) and \(\left( {M + 3} \right) \times 1\). The last cow of A represents the convex combination of paraments. We definite an augmented matrix \(\bar{\mathbf{A}} = \left[ {{\mathbf{A}}\left| {\mathbf{b}} \right. } \right] \). Recalling that the last elements of the first \(\left( {M + 2} \right) \) rows are all zero and \(\left| {\mathcal{K}} \right| \le M + 2\), the last row of matrix \({\bar{\mathbf{A}}}\) can always be transformed into \(\left[ {{{\mathbf{0 }}_{1 \times \left| {\mathcal{K}} \right| }}\left| b \right. } \right] \), where \(b \ne 0\). Hence, there is no \({\varvec{\uptheta }}\) existing to satisfy equations \({A{\varvec{\uptheta } }} = {\mathbf{b}}\). Now we finish the proof.
Rights and permissions
About this article
Cite this article
Zhang, X., Guo, D., An, K. et al. Secure transmission and power allocation in multiuser distributed massive MIMO systems. Wireless Netw 26, 941–954 (2020). https://doi.org/10.1007/s11276-018-1840-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-018-1840-y