Abstract
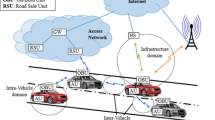
The relay-node selection plays a decisive impact on the message dissemination in vehicular network. However, in some scenarios, due to lack of the reliable and stable relay-node selection, the message dissemination suffers from an intolerable delay, even a failure. In this paper, we focus on a design of the robust relay selection, which aims at (1) achieving a maximum message dissemination speed in general scenarios, and (2) assuring an acceptable dissemination speed in the adverse scenario. Two adverse scenarios are first introduced for the message dissemination when the distance-based relay selection is applied in multi-hop broadcast. To tackle the challenge, we propose a robust distance-based relay selection by optimizing the exponent-based partitioning broadcast protocol (our previous work) and incorporating a proposed mini-black-burst-assisted mechanism. Moreover, we develop analytic models for the robust approach performances in terms of contention latency and packet delivery ratio (PDR). Simulations are used to verify these analytic models, demonstrate the acceptable performances of the proposal in adverse scenarios, and compare it with the state-of-the-art approaches in general scenarios. Results show an increase of more than 11.01% in terms of message dissemination speed independent of vehicle density and a stable PDR of more than 99.99%.








Similar content being viewed by others
References
Maglaras, L. A., Al-Bayatti, A. H., He, Ying, Wagner, I., & Janicke, H. (2016). Social internet of vehicles for smart cities. Journal of Sensor and Actuator Networks, 5(1), 3.
Bitam, S., Mellouk, A., & Zeadally, S. (2015). Bio-inspired routing algorithms survey for vehicular ad hoc networks. IEEE Communications Surveys and Tutorials, 17(2), 843–867.
Karagiannis, G., Altintas, O., Ekici, E., Heijenk, G., Jarupan, B., Lin, K., et al. (2011). Vehicular networking: A survey and tutorial on requirements, architectures, challenges, standards and solutions. IEEE Communications Surveys and Tutorials, 13(4), 584–616.
Rehman, S. U., Khan, M. A., & Zia, T. A. (2015). A multi-hop cross layer decision based routing for vanets. Wireless Networks, 21(5), 1647–1660.
Ji, B., Song, K., Zhu, J., & Li, W. (2014). Efficient mac protocol design and performance analysis for dense wlans. Wireless Networks, 20(8), 2237–2254.
Zhao, N., Yu, F. R., Sun, H., Yin, H., & Nallanathan, A. (2015). Interference alignment with delayed channel state information and dynamic ar-model channel prediction in wireless networks. Wireless Networks, 21(4), 1227–1242.
Zheng, K., Zheng, Q., Chatzimisios, P., Xiang, W., & Zhou, Y. (2015). Heterogeneous vehicular networking: A survey on architecture, challenges, and solutions. IEEE Communications Surveys and Tutorials, 17(4), 2377–2396.
Long, M., Chen, Y., & Renzo, M. D. (2014). Performance analysis of relay selection in the presence of on Coff relay traffic. IEEE Transactions on Vehicular Technology, 63(6), 2959–2964.
Ma, X., Zhang, J., Yin, X., & Trivedi, K. S. (2012). Design and analysis of a robust broadcast scheme for vanet safety-related services. IEEE Transactions on Vehicular Technology, 61(1), 46–61.
Jabbarpour, M. R., Jalooli, A., Shaghaghi, E., Marefat, A., Noor, R. M., & Jung, J. J. (2014). Analyzing the impacts of velocity and density on intelligent position-based routing protocols. Journal of Computational Science, 11(2), 177–184.
Fogue, M., Garrido, P., Martinez, F. J., Cano, J. C., Calafate, C. T., & Manzoni, P. (2013). Identifying the key factors affecting warning message dissemination in vanet real urban scenarios. Sensors, 13(4), 5220.
Cao, D., Lei, Z., Baofeng, J. I., & Chunguo, L. I. (2016). Exponent-based partitioning broadcast protocol for emergency message dissemination in vehicular networks. IEICE Transactions on Fundamentals, E99.A(11), 2075–2083.
Bilal, S. M., Bernardos, C. J., & Guerrero, C. (2013). Position-based routing in vehicular networks: A survey. Journal of Network and Computer Applications, 36(2), 685C697.
Sahoo, J., Wu, H. K., Sahu, P. K., & Gerla, M. (2011). Binary-partition-assisted mac-layer broadcast for emergency message dissemination in vanets. IEEE Transactions on Intelligent Transportation Systems, 12(3), 757–770.
Suthaputchakun, C., Dianati, M., & Sun, Z. (2014). Trinary partitioned black-burst-based broadcast protocol for time-critical emergency message dissemination in vanets. IEEE Transactions on Vehicular Technology, 63(6), 2926–2940.
Ni, S. Y., Tseng, Y. C., Chen, Y. S., & Sheu, J. P. (1999). The broadcast storm problem in a mobile ad hoc network. ACM/IEEE International Conference on Mobile Computing and Networking, 8, 151–162.
Korkmaz, G., Ekici, E., & Ozguner, F. (2007). Black-burst-based multihop broadcast protocols for vehicular networks. IEEE Transactions on Vehicular Technology, 56(5), 3159–3167.
Bi, Y., Zhao, H., & Shen, X. (2009). A directional broadcast protocol for emergency message exchange in inter-vehicle communications. In IEEE International conference on communications (pp. 1-5). IEEE.
Salvo, P., De Felice, M., Baiocchi, A., Cuomo, F., & Rubin, I. (2013). Timer-based distributed dissemination protocols for VANETs and their interaction with MAC layer. In Vehicular technology conference (Vol. 14, pp. 1–6). IEEE.
Sobrinho, J. L., & Krishnakumar, A. S. (1996). Distributed multiple access procedures to provide voice communications over IEEE 802.11 wireless networks. In Proceedings of the GLOBECOM’96, London, UK (pp. 1689–1694).
Tian, D., Zhou, J., Wang, Y., Zhang, G., & Xia, H. (2015). An adaptive vehicular epidemic routing method based on attractor selection model. Ad Hoc Networks, 36(P2), 465–481.
Baiocchi, A., Salvo, P., Cuomo, F., & Rubin, I. (2016). Understanding spurious message forwarding in vanet beaconless dissemination protocols: An analytical approach. IEEE Transactions on Vehicular Technology, 65(4), 2243–2258.
Tables of Speed and Stopping Distances, the State of Virginia [Online]. (2018). https://law.lis.virginia.gov/vacode/46.2-880/. Accessed April 12 2018.
Regulations for the Implementation of the Road Traffic Safety Law in People’s Republic of China [Online]. (2018). http://www.gov.cn/banshi/2005-08/23/content_25579_3.htm. Accessed April 12 2018.
Moral, P. D., Doucet, A., & Jasra, A. (2006). Sequential monte carlo samplers. Journal of the Royal Statistical Society, 68(3), 411–436.
Reis, A. B., Sargento, S., Neves, F., & Tonguz, O. K. (2014). Deploying roadside units in sparse vehicular networks: What really works and what does not. IEEE Transactions on Vehicular Technology, 63(6), 2794–2806.
Shah, V., Mehta, N. B., & Yim, R. (2009). Optimal timer based selection schemes. IEEE Transactions on Communications, 58(6), 1814–1823.
Acknowledgements
We thank the reviewers for their helpful comments and the National Natural Science Foundation of China (Grant Nos. 51675059, 51408069, 61702052 and U1404615), Open Funds of State Key Laboratory of Millimeter Waves (Grant No. K201504), China Postdoctoral Science Foundation (Grant No. 2015M571637), and Science and Technology Project of Hunan Province (Grant No. 2015JC3057) for their support.
Author information
Authors and Affiliations
Corresponding author
Appendix: Optimization of EPBP
Appendix: Optimization of EPBP
This section provides the optimization of EPBP with A. As mentioned in Sect. 4.1, we determine the optimal value \({A_{{\mathrm{opt}}}}\) of A to maximize the average message dissemination speed \({v_{{\mathrm{ave}}}}\) when \(N_{{\mathrm{iter}}}=1\). \({A_{{\mathrm{opt}}}}\) can be derived in the following equation,
The index i of the i-th vehicle density \({\lambda _i}\) for all metrics is omitted for simple presentation.
1.1 Message progress \(\beta \)
\(\beta \) can be attained as
where
is the average message progress if the k-th segment is the final segment, and
is the probability of the selection of the k-th segment. \({\mu _{{\mathrm{seg\_bro}}}}(k)\) in (29) is the vehicle number in other segments in the message broadcasting direction of the k-th segment, which can be achieved as
1.2 One-hop delay \({T_{\mathrm{d}}}\)
\({T_{\mathrm{d}}}\) can be attained as
where \({T_{{\mathrm{init}}}}\), \({T_{{\mathrm{part}}}}\), \({T_{{\mathrm{cont}}}}\) and \({T_{{\mathrm{data}}}}\) are the initial latency, the partitioning latency, the contention latency and the data transmission latency, respectively. Among the four latencies, the selection of A can affect the value of \({T_{{\mathrm{part}}}}\) and \({T_{{\mathrm{cont}}}}\). They can be attained as
where
is the number of time slots spent when the k-th segment is selected. And
is the average contention latency when the k-th segment is the final segment. It is noted that \({T_{{\mathrm{cont}\_\mathrm{seg}}}}\) in (35) differs from that in (16) since the exponential back-off timer isn’t adopted in the optimization here.
1.3 Expression of \(\frac{{{\mathrm{d}} \beta }}{{{\mathrm{d}} A}}\)
From (27), \(\frac{{{\mathrm{d}} \beta }}{{{\mathrm{d}} A}}\) in (26) can be achieved as
where
In (37),
and
1.4 Expression of \(\frac{{{\mathrm{d}} {T_{\mathrm{d}}}}}{{{\mathrm{d}} A}}\)
From (31), \(\frac{{{\mathrm{d}} {T_{\mathrm{d}}}}}{{{\mathrm{d}} A}}\) in (26) can be achieved as
where
In (43),
Rights and permissions
About this article
Cite this article
Cao, D., Zheng, B., Ji, B. et al. A robust distance-based relay selection for message dissemination in vehicular network. Wireless Netw 26, 1755–1771 (2020). https://doi.org/10.1007/s11276-018-1863-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-018-1863-4