On optimal relaying strategies for VANETs over double Nakagami-m fading channels

Abstract

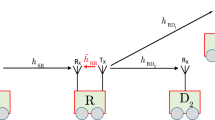
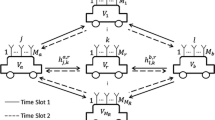
Vehicular ad hoc networks (VANETs) are able to facilitate data exchange among vehicles and provide diverse data services. The benefits of cooperative communications are such as to make it a proper idea to improve the achievable rate and diversity in VANETs. We investigate a dual-hop relay vehicular network with different transmit powers in vehicles on non-uniform shadowed double Nakagami-m fading channels in the presence of non-uniform co-channel interferers. In this paper, we investigate the diversity-multiplexing tradeoff (DMT) in such a network for three different schemes, namely, dynamic decode and forward (DDF), dynamic quantize map and forward and static quantize map and forward and prove that the DDF strategy has the optimal DMT. Also, the optimal listening and transmitting time of vehicles in various strategies as a function of the channel conditions in vehicles are determined. Finally, we extend our results to a general multi-hop relay vehicular network model with multiple half-duplex relay terminals and different average SNRs over links.

Appendices

Appendix 1: DMT of full-duplex network

In this section, we calculate the DMT of two-hop full-duplex relay network. For a FD relay channel, if all the nodes in the network know the channel realizations $h_{SR_1}$ and $h_{R_1D}$, the information theoretical cut-set upper bound $C_u(\rho ^a, \rho ^b)$ on the achievable rate of the link $S-D$ with a constant additive gap is given by

$$\begin{aligned} C_u&=\min {\{\log (1+{|h_{SR_1 } |}^2\rho ^a ), } \log (1+{|h_{R_1D} |}^2\rho ^b )\}. \end{aligned}$$

(41)

We can find $d_{FD}(r)$ of a full-duplex network by solving the problem:

$$\begin{aligned} d_{FD}(r)=-\lim _{\rho \rightarrow \infty }\frac{\Pr \{C_u\le r\log \rho \}}{\log \rho }. \end{aligned}$$

(42)

The exponential orders of the instantaneous SNRs for $S{-}R_1$ and $R_1{-}D$ links are defined as

$$\begin{aligned} \alpha&=\frac{\log (|h_{SR_1}|^2\rho ^a)}{\log \rho }, \quad \beta =\frac{\log (|h_{R_1D}|^2\rho ^b)}{\log \rho }. \end{aligned}$$

(43)

In this case, the outage event, $C_u<r\log \rho$, at the high SNR regime is equivalent to having $\min (\alpha ^+,\beta ^+) < r\log \rho$. Using the joint probability density function (pdf) of the random variables $(\alpha ,\beta )$ and after some simplifications in a manner similar to [27], we come up with the following optimization problem:

$$\begin{aligned} d_{FD}(r) =&\min _{(\alpha ,\beta ):\{\min (\alpha ,\beta )\le r,0\le \alpha \le a,0\le \beta \le b\}} m_1(a-\alpha )^++m_2(b-\beta )^+, \end{aligned}$$

(44)

We can split the optimization problem (44) into three separate optimizations as follows:

$$\begin{aligned} S_1&=\min _{(\alpha ,\beta )} m_1(a-\alpha )^++m_2(b-\beta )^+, \quad {\text {s.t.}}~~ \{\alpha \le r,0\le \alpha \le a,0\le \beta \le b\},\\ S_2&=\min _{(\alpha ,\beta )} m_1(a-\alpha )^++m_2(b-\beta )^+, \quad {\text {s.t.}}~~ \{ \beta \le r,0\le \alpha \le a,0\le \beta \le b \}. \end{aligned}$$

Note that in the optimization problem $S_1$ and $0\le \beta \le b$ are the only constraints on $\beta$ hence, the best options are $\beta = b$, thus, we have $S_1=m_1{(a-r)}^+$. With a similar argument as in $S_1$ for the optimization problems $S_2$, $d_{FD}(r)$ of a half-duplex linear network is achieved as

$$\begin{aligned} d_{FD}(r)=\min \{ S_1,S_2\}=\min \left\{ {m_1(a-r)}^+,{m_2(b-r)}^+ \right\} , \end{aligned}$$

(45)

and this completes the proof of the Proposition 1.

Appendix 2: DMT of DDF strategy

We calculate the DMT of a two-hop HD relay vehicular network when the relay vehicle uses the DDF protocol.

For simplicity, we assume $\eta _1=\rho ^a$ and $\eta _2=\rho ^b$ then, we have $\gamma _i=\frac{\eta _i \mid h_i\mid ^2}{N_0}, i=1,2$. By using (2), the pdf of the channel power gain $\gamma _i, i=1,2$ is obtained as

$$\begin{aligned} f_{\gamma _i}(x)& = f_h(x)|dh/dx|\end{aligned}$$

(46)

$$\begin{aligned}& = \frac{2(m_{i,1}m_{i,2})^{(m_{i,1}+m_{i,2})/2}}{\eta _i\varGamma (m_{i,1})\varGamma (m_{i,2})}\left(\frac{x}{\eta _i}\right)^{(m_{i,1}+m_{i,2}-2)/2} \\&\quad K_{(m_{i,2}-m_{i,1})}\left( 2\sqrt{m_{i,1}m_{i,2}\frac{x}{\eta _i}}\right) ,\ \ i=1,2. \end{aligned}$$

(47)

Let us express the modified Bessel function $K_{(m_{i,2}-m_{i,1})}\left( 2\sqrt{m_{i,1}m_{i,2}\frac{x}{\eta _i}}\right)$ according to the Meijer-G function as [41],

$$\begin{aligned}&K_{(m_{i,2}-m_{i,1})}\left( 2\sqrt{m_{i,1}m_{i,2}\frac{x}{\eta _i}}\right) \\&\quad =\frac{1}{2}G_{0,2}^{2,0}\Bigg (m_{i,1}m_{i,2}\frac{x}{\eta _i}\Bigg |\begin{array}{ccc} 0,0 \\ \frac{m_{i,1}-m{i,2}}{2},\frac{m_{i,2}-m{i,1}}{2} \\ \end{array}\Bigg ) \end{aligned}$$

(48)

By using the hyper-geometric function in Meijer-G function [42] and simplifying it, we have,

$$\begin{aligned} f_{ \gamma _i}(x)&=\sum _{k=0}^\infty \frac{c_{i,k}(m_{i,1}, m_{i,2})}{\eta _i}\left(\frac{x}{\eta _i}\right)^{k+m_{i,2}-1} \\&\quad +\sum _{k=0}^\infty \frac{c_{i,k}(m_{i,2}, m_{i,1})}{\eta _i}\left(\frac{x}{\eta _i}\right)^{k+m_{i,1}-1}, \quad i=1,2 \end{aligned}$$

(49)

where $c_{i,k}$ is as

$$\begin{aligned} c_{i,k}(m_{i,1}, m_{i,2})=2\frac{(m_{i,1}m_{i,2})^{m_{i,2}+i}\varGamma (m_{i,1}-m_{i,2})}{\varGamma ({m_{i,1}})\varGamma ({m_{i,2}})(1+m_{i,2}-m_{i,1})_k\ k!}, \quad i=1,2 \end{aligned}$$

(50)

and $(v)_n$ is the Pochhammer symbol defined in [41].

Having $\eta _1=\rho ^a$, $\eta _2=\rho ^b$, $\gamma _1=\rho ^\alpha$, $\gamma _2=\rho ^\beta$ and for the high SNR the pdf of double Nakagami-m distribution over $S-R-D$ channel can be obtained as

$$\begin{aligned} f_{\alpha , \beta }(\alpha , \beta )\doteq \frac{c_{1,0}(m_{1,2},m_{1,1})}{\rho ^a}\frac{c_{2,0}(m_{2,2},m_{2,1})}{\rho ^b}\rho ^{(\alpha -a)(\min \{m_{1,1},m_{1,2}\}-1)}\rho ^{(\beta -b)(\min \{m_{2,1},m_{2,2}\}-1)} \end{aligned}$$

(51)

We state the outage event at the destination D as the situation that any message cannot be recovered by D. Thus, the overall outage probability of the DDF protocol for high SNR at the destination is denoted as

$$\begin{aligned} P_{out-DDF}&=Pr( (C_{S-R}<R) \text { or } (C_{S-R}>R, C_{R-D}<R)) \\&=\int \int _{O_1(r,t)\bigcup O_2(r,t)}\frac{c_{1,0}}{\rho ^a}\frac{c_{2,0}}{\rho ^b}\rho ^{\min \{m_{1,1},m_{1,2}\}(\alpha -a)}\rho ^{\min \{m_{2,1},m_{2,2}\}(\beta -b)} d\alpha d\beta , \end{aligned}$$

(52)

where

$$\begin{aligned}&O_1(r,t)= \left\{ (\alpha ,\beta ) \mid 0{\le }\alpha {\le }a,0{\le }\beta {\le }b,\frac{r}{\alpha }{\ge }1\right\}, \\&O_2(r,t)= \left\{(\alpha ,\beta ) \mid 0\le \alpha {\le }a,0\le \beta {\le }b,\frac{ r}{\alpha }<1, \frac{r}{\alpha }+\frac{r}{\beta }{\ge }1\right\}, \end{aligned}$$

(53)

where $O_i (r,t),i=1,2$ are the outage regions of two events that are occurred in the network as in Sect. 4.1. In (52), the integral is conquered by the term with the largest SNR exponent for when the SNR tends to infinity. Therefore, by using Laplace’s principle in [19], the DMT in (8) for the HD relay can be obtained as

$$\begin{aligned} d_{{\mathrm {DDF}}}(r)& = - \lim _{\rho \rightarrow \infty }\frac{ \log P_{out-DDF}(\rho ^ a, \rho ^b )}{\log \rho } \end{aligned}$$

(54)

$$\begin{aligned}& = \min _{(\alpha ,\beta )\in O(r,t) } \big ( m_1(a-\alpha )^++m_2(b-\beta )^+\big ), \end{aligned}$$

(55)

where $m_1=\min (m_{1,1},m_{1,2})$, $m_2=\min (m_{2,1},m_{2,2})$ and also we have,

$$O(r) = \left \{(\alpha ,\beta ) \mid 0\le \alpha \le a,0\le \beta \le b, \left(\left(\frac{r}{\alpha }\ge 1\right) \quad {\text {or}} \quad \left(\frac{ r}{\alpha } < 1,\frac{ r}{\alpha }+\frac{r}{\beta }\ge 1\right)\right)\right\}. $$

This completes the proof of the DMT problem with the DDF protocol in Sect. 4.1.

Appendix 3: DMT of DQMF strategy

All rates less than $\max _{t(h_{1},h_{2})}C(\rho ^a,\rho ^b)-K_2$ are achievable with the DQMF scheme with global CSI as in Sect. 4.2. Thus, the outage probability for the high SNR is obtained as

$$\begin{aligned} \lim _{\rho \rightarrow \infty }P_{out}\left(\rho ^ a, \rho ^b \right)&=\lim _{\rho \rightarrow \infty }Pr\left(\max _{t\left(h_{1},h_{2}\right)}C\left(\rho ^a,\rho ^b\right)\le r\log \rho \right) \\&=\lim _{\rho \rightarrow \infty }Pr\left(\max _{t(h_{1},h_{2})}\min \{t\alpha , (1-t)\beta \}\le r\right) \\&=\lim _{\rho \rightarrow \infty }\int \int _{\max _{t(h_{1},h_{2})}\min \{t\alpha , (1-t)\beta \}\le r}f_{\alpha , \beta }(\alpha , \beta )d\alpha d\beta \end{aligned}$$

(56)

where $f_{\alpha , \beta }(\alpha , \beta )$ is given in (51). By using similar steps as “Appendix 1” section, the DMT of the DQMF strategy with global CSI is obtained as

$$\begin{aligned} d_{DQMF-G} (r)&=\min _{(\alpha ,\beta )\in O(r,t) } \big ( m_1(a-\alpha )^++m_2(b-\beta )^+\big ), \end{aligned}$$

(57)

where

$$\begin{aligned} O(r,t) &= \left \{(\alpha ,\beta ) \mid 0\le \alpha \le a,0\le \beta \le b, \max _{t(h_{1},h_{2})}\min \{t\alpha , (1-t)\beta \}\le r\right\}. \end{aligned}$$

The optimal choice for t is achieved by $t\alpha =(1-t)\beta$. This results in (25).

Appendix 4: DMT of SQMF strategy

In [14], it is shown that the rate achieved by SQMF where the relay vehicle listens with a fixed schedule is lower of $C(\rho ^a,\rho ^b)-K_2$. The time of the listening and transmitting t in the SQMF strategy are selected as it can minimize the outage without the aware of instantaneous CSI. Thus, the optimal probability of outage for the high SNR regime is characterized as

$$\begin{aligned} \min _{0\le t\le 1}\lim _{\rho \rightarrow \infty }P_{out}(\rho ^ a, \rho ^b )&=\lim _{\rho \rightarrow \infty }\Pr (C(\rho ^a,\rho ^b)-K_2\le r\log \rho ) \\&=\min _{0\le t\le 1}\int \int _{\min \{t\alpha , (1-t)\beta \}\le r} f_{\alpha , \beta }(\alpha , \beta ) d\alpha d\beta \\&=\min _{0\le t\le 1} \ \ \max _{\begin{array}{c} \min \{t\alpha , (1-t)\beta \}\le r, \\ 0\le \alpha \le a,0\le \beta \le b \end{array}}\rho ^{\big (m_1 (a-\alpha )^++m_2(b-\beta )^+\big )} \\&=\rho ^{-d_{{\mathrm {SQMF}}}(r)}, \end{aligned}$$

(58)

where by using Laplace’s method of integration [19], the the $d_{SQMF}(r)$ exponent is given by

$$\begin{aligned}&d_{{\mathrm {SQMF}}}(r) = \max _{0\le t\le 1} \ \ \min _{\begin{array}{c} 0\le \alpha \le a,0\le \beta \le b,\\ \min (t\alpha ,(1-t)\beta )\le r \end{array}}\big (m_1 (a-\alpha )^++m_2 (b-\beta )^+\big ). \end{aligned}$$

(59)

Appendix 5: Proof of Corollary 1

To compute the ratio $\zeta (r)=\frac{d_{{\mathrm {DDF}}}(r)}{d_{{\mathrm {SQMF}}}(r)}$ in a two-hop relay vehicular network with same shape parameter over links ($m=m_1=m_2$), we calculate the DMT of the DDF and SQMF strategies in Sect. 4 and then, we prove that $\zeta (r) \le 2$. In this regard, we must examine two cases, then we prove that the above inequality is valid for each case.

1)For the case $b>a$, the inequality $\frac{d_{{\mathrm {DDF}}}(r)}{d_{{\mathrm {SQMF}}}(r)}\le 2$ is calculated as

$$\begin{aligned} \zeta (r) = \frac{a-\frac{rb}{b-r}}{\frac{1}{2}(b + a -2 r - \sqrt{b^2 - 2ba+ a^2 + 4r^2 })} \le 2. \end{aligned}$$

(60)

Then, we can obtain

$$\begin{aligned} (2ba-a^2+3b^2)r^2+(-4ab^2+2ba^2-2b^3)r-b^2a^2+2ab^3 \ge 0. \end{aligned}$$

(61)

The above inequality is valid only if $0<r<\frac{ab}{a+b} \ {\text {or}} \ r>\frac{-2b^2+ba}{a-3b}$ and thus (60) is true.

2)If $a>b$. The DMT is given as $d_{{\mathrm {DDF}}}(r)=b-\frac{ra}{a-r}$ and we can show that inequality $\zeta (r)\le 2$ is equivalent to

$$\begin{aligned} (2ba-b^2+3a^2)r^2+(-4ba^2+2ab^2-2a^3)r-a^2b^2+2ba^3 \ge 0, \end{aligned}$$

(62)

then, the inequality (62) is valid only if $0<r<\frac{ab}{a+b} \ {\text {or}} \ r>\frac{-2a^2+ba}{b-3a}$. Similar to previous cases, the DMTs ratio of the DDF and SQMF schemes is less than or equal 2 and this completes the proof of Corollary 1 in Sect. 3.