Abstract
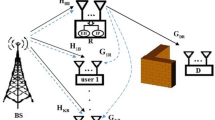
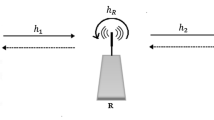
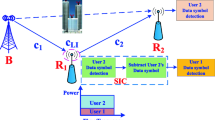
To serve massive connections in heterogeneous networks with respect to higher energy efficiency, we focus on new paradigm in order to achieve multiple access and performance improvement at cell-edge area. The power domain based non-orthogonal multiple access is introduced to address such problem. In particular, this paper studies a self-energy relay together with full-duplex scheme to implement cooperative power domain based non-orthogonal multiple access in small-cell system of the heterogeneous networks. In such small-cell network, a nearby user can be employed as a decode-and-forward with self-energy recycling protocol to assist a far power domain based non-orthogonal multiple access user (cell-edge user). The relay harvests energy from dedicated energy signal sent by a base station, while it still reuses energy from loop self-interference signal. To characterize the performance of the proposed system with respect to where meets weak signal condition, numerous expressions of exact outage probability for far power domain based non-orthogonal multiple access user is derived. Several practical scenarios are performed in three different schemes related to how energy harvesting architecture can be achieved. Based on analytical results, the optimal throughput achieved by the cell-edge user in small-cell network can be observed. Numerical results are presented to validate the accuracy of the derived results.











Similar content being viewed by others
References
Ding, Z., Lei, X., Karagiannidis, G. K., Schober, R., Yuan, J., & Bhargava, V. (2017). A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE Journal on Selected Areas in Communications, 35(10), 2181–2195.
Liu, Y., Qin, Z., Elkashlan, M., Ding, Z., Nallanathan, A., & Hanzo, L. (2017). Nonorthogonal multiple access for 5G and beyond. Proceedings of the IEEE, 105(12), 2347–2381.
Do, D.-T., & Van Nguyen, M.-S. (2019). Device-to-device transmission modes in NOMA network with and without wireless power transfer. Computer Communications, 139, 67–77.
Do, D.-T., Le, A.-T., & Lee, B. M. (2020). NOMA in cooperative underlay cognitive radio networks under imperfect SIC. IEEE Access, 8, 86180–86195.
Do, D.-T., Vaezi, M., & Nguyen, T.-L. (2018). Wireless powered cooperative relaying using NOMA with imperfect CSI. In Proceedings of the IEEE Globecom workshops (GC Wkshps), Abu Dhabi, UAE (pp. 1–6).
Islam, S. M. R., Avazov, N., Dobre, O. A., & Kwak, K.-S. (2017). Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Communications Surveys and Tutorials, 19(2), 721–742.
Nikopour, H. et al. (2014). SCMA for downlink multiple access of 5G wireless networks. In Proceedings of the IEEE global communications conference (GLOBECOM), Austin, TX, USA (pp. 3940–3945).
Ling, B., Dong, C., Dai, J., & Lin, J. (2017). Multiple decision aided successive interference cancellation receiver for NOMA systems. IEEE Wireless Communications Letters, 6(4), 498–501.
Kschischang, F. R., Frey, B. J., & Loeliger, H.-A. (2001). JFactor graphs and the sum-product algorithm. IEEE Transactions on Information Theory, 47(2), 498–519.
Moltafet, M., Yamchi, N. M., Javan, M. R., & Azmi, P. (2018). Comparison study between PD-NOMA and SCMA. IEEE Transactions on Vehicular Technology, 67(2), 1830–1834.
Moltafet, M., Mokari, N., Javan, M. R., Saeedi, H., & Pishro-Nik, H. (2018). A new multiple access technique for 5G: Power domain sparse code multiple access (PSMA). IEEE Access, 6, 747–759.
Do, Dinh-Thuan. (2015). Energy-aware two-way relaying networks under imperfect hardware: Optimal throughput design and analysis. Telecommunication Systems, 62(2), 449–459.
Do, D.-T., Nguyen, H.-S., Voznak, M., & Nguyen, T.-S. (2017). Wireless powered relaying networks under imperfect channel state information: System performance and optimal policy for instantaneous rate. Radioengineering, 26(3), 869–877.
Do, D.-T., Nguyen, H.-S. (2016). A tractable approach to analyze the energy-aware two-way relaying networks in presence of co-channel interference. EURASIP Journal on Wireless Communications and Networking.
Nguyen, T.-L., & Do, D.-T. (2018). Exploiting impacts of intercell interference on SWIPT-assisted non-orthogonal multiple access. Wireless Communications and Mobile Computing, 2018, Article ID 2525492.
Nguyen, X.-X., & Do, Dinh-Thuan. (2017). Maximum harvested energy policy in full-duplex relaying networks with SWIPT. International Journal of Communication Systems, 30, 17.
Do, D.-T., Van Nguyen, M.-S., Hoang, T.-A., & Lee, B.-M. (2019). Exploiting joint base station equipped multiple antenna and full-duplex D2D users in power domain division based multiple access networks. Sensors (Basel), 19(11), 2475.
Zhang, Z., Ma, Z., Xiao, M., Ding, Z., & Fan, P. (2017). Full-duplex device-to-device-aided cooperative non-orthogonal multiple access. IEEE Transactions on Vehicular Technology, 66(5), 4467–4471.
Sun, Q., Han, S. F., Chin-Lin, I., & Pan, Z. G. (2015). On the ergodic capacity of MIMO NOMA systems. IEEE Wireless Communications Letters, 4(4), 405–408.
Ding, Z., Yang, Z., Fan, P., & Poor, H. V. (2014). On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Processing Letters, 21(12), 1501–1505.
Dang, H.-P., Van Nguyen, M., Do, D.-T., Pham, H. L., Selim, B., & Kaddoum, G. (2020). Joint relay selection, full-duplex and device-to-device transmission in wireless powered NOMA networks. IEEE Access, 8, 82442–82460.
Peng, M., et al. (2016). Recent advances in cloud radio access networks: System architectures, key techniques, and open issues. IEEE Communications Surveys and Tutorials, 18(3), 2282–2308.
Vien, Q. T., Ogbonna, N., Nguyen, H. X., Trestian, R., & Shah, P. (2015). Non-orthogonal multiple access for wireless downlink in cloud radio access networks. In Proceedings of the IEEE EW 2015, Budapest, Hungary (pp. 434–439).
Chingoska, H., Hadzi-Velkov, Z., Nikoloska, I., & Zlatanov, N. (2016). Resource allocation in wireless powered communication networks with non-orthogonal multiple access. IEEE Wireless Communications Letters, 5(6), 684–687.
Diamantoulakis, P. D., Pappi, K. N., Ding, Z., & Karagiannidis, G. K. (2016). Wireless-powered communications with non-orthogonal multiple access. IEEE Transactions on Wireless Communications, 15(12), 8422–8436.
Diamantoulakis, P. D., Pappi, K. N., Karagiannidis, G. K., Xing, H., & Nallanathan, A. (2017). Joint downlink/uplink design for wireless powered networks with interference. IEEE Access, 5, 1534–1547.
Zewde, T. A., & Gursoy, M. C. (2018). NOMA-based energy-efficient wireless powered communications. IEEE Transactions on Green Communications and Networking, 2(3), 679–692.
Gong, J., & Chen, X. (2017). Achievable rate region of non-orthogonal multiple access systems with wireless powered decoder. IEEE Journal on Selected Areas in Communications, 35(12), 2846–2859.
Sun, H., Zhou, F., Hu, R. Q., & Hanzo, L. (2019). Robust beamforming design in a NOMA cognitive radio network relying on SWIPT. IEEE Journal on Selected Areas in Communications, 37(1), 142–155.
Liu, Y., Ding, Z., Elkashlan, M., & Poor, H. V. (2016). Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer. IEEE Journal on Selected Areas in Communications, 34(4), 938–953.
Dai, L., Wang, B., Peng, M., & Chen, S. (2019). Hybrid precoding-based millimeter-wave massive MIMO-NOMA with simultaneous wireless information and power transfer. IEEE Journal on Selected Areas in Communications, 37(1), 131–141.
Boshkovska, E., Ng, D. W. K., Zlatanov, N., & Schober, R. (2015). Practical non-linear energy harvesting model and resource allocation for SWIPT systems. IEEE Communications Letters, 19(12), 2082–2085.
Boshkovska, E., Morsi, R., Ng, D. W. K., & Schober, R. (2016). Power allocation and scheduling for SWIPT systems with non-linear energy harvesting model. In Proceedings of the IEEE international conference on communication (pp. 1–6).
Boshkovska, E., Ng, D. W. K., Zlatanov, N., Koelpin, A., & Schober, R. (2017). Robust resource allocation for MIMO wireless powered communication networks based on a non-linear EH model. IEEE Transactions on Communications, 65(5), 1984–1999.
Muhammad, F., Abbas, Z. H., & Li, F. Y. (2017). Cell association with load balancing in nonuniform heterogeneous cellular networks: Coverage probability and rate analysis. IEEE Transactions on Vehicular Technology, 66(6), 5241–5255.
Dhillon, H. S., Ganti, R. K., Baccelli, F., & Andrews, J. G. (2012). Modeling and analysis of K-tier downlink heterogeneous cellular networks. IEEE Journal on Selected Areas in Communications, 30(3), 550–560.
Wang, H., Zhou, X., & Reed, M. C. (2014). Coverage and throughput analysis with a non-uniform small cell deployment. IEEE Transactions on Wireless Communications, 13(4), 2047–2059.
Wu, H., Tao, X., Xu, J., & Li, N. (2015). Coverage analysis for comp in two tier hetnets with non-uniformly deployed femtocells. IEEE Communications Letters, 19(9), 1600–1603.
Han, S., Yang, C., & Chen, P. (2015). Full duplex-assisted intercell interference cancellation in heterogeneous networks. IEEE Transactions on Communications, 63(12), 5218–5234.
Wildemeersch, M., Quek, T. Q. S., Kountouris, M., Rabbachin, A., & Slump, C. H. (2014). Successive interference cancellation in heterogeneous networks. IEEE Transactions on Communications, 62(12), 4440–4453.
Chen, L., Ma, L., Xu, Y., & Leung, V. C. M. (2019). Hypergraph spectral clustering based spectrum resource allocation for dense NOMA-HetNet. IEEE Wireless Communications Letters, 8(1), 305–308.
Nasser, A., Muta, O., Elsabrouty, M., & Gacanin, H. (2019). Interference mitigation and power allocation scheme for downlink MIMO-NOMA HetNet. IEEE Transactions on Vehicular Technology, 68(7), 6805–6816.
Arfken, G. (1985). Taylor’s expansion. In G. B. Arfken, H. J. Weber, & F. E. Harris (Eds.), Mathematical methods for physicists (3rd ed., pp. 303–313). Orlando, FL: Academic Press.
Zwillinger, D. (2014). Table of integrals, series, and products. Amsterdam: Elsevier.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Proof of Proposition 1
The outage probability can be expressed as
We first recall expression of \( I_1 \) as
Then, after performing manipulations, it can be given by
where \(A = \frac{{\left( {{a_2} - {\gamma _{th2}}{a_1}} \right) }}{{{\gamma _{th2}}a}}\), \(B = \frac{{d_1^m{P_{\min }}}}{{{P_S}}}\), \(C = \frac{{d_1^m{P_{{\mathrm{max}}}}}}{{{P_S}}}\) and \(D = \frac{{{\gamma _{th2}}d_1^m\xi _d}}{{a{P_S}}}\) . Considering x as integration variable, by employing exponential distribution for \({h_i}\), i.e. the CDF and PDF as considerations in (1),(2). As a result, \({I_1}\) can be formulated as
Similar to \({I_1}\), we can epress \({I_2}\) as:
It is noted that \({P_{input}} = \frac{{{P_S}{{\left| {{h_1}} \right| }^2}}}{{d_1^m}}\), (11) and (12), \({I_2}\) can be further expressed as
where \(E = \frac{{\xi _d{\gamma _{th2}}}}{{a{P_{{\mathrm{max}}}}}}\).
In this step, (41) can be transformed as
With help (1) and (2), \({I_2}\) can be shown in closed-form as:
This is end of the proof. \(\square \)
Appendix 2
In the HDNL mode, the components of outage probability can be clarified as below. It is noted that such outage event is given by
To address such outage behavior, \(L_1\) and \(L_2\) can be defined as:
and
With help (19), (20) and putting them into (46). Then, we can be obtained as:
where \({D^{HD}} = \frac{{\gamma _{th2}^{HD}d_1^m\xi _d}}{{a{P_S}}}\), \(F = \frac{{{\gamma _{th2}^{HD}}\xi _r}}{{{a_2}{P_S} - {\gamma _{th2}}{a_1}{P_S}}}\). Then, \(L_1\) can be written as
By using the expanded Taylor’s series [43, Eq. 5.90], it follows that \({e^{\left( { - \frac{a}{x}} \right) }} = \sum \nolimits _{k = 0}^{{N_t}} {\frac{{{{\left( { - 1} \right) }^k}}}{{k!}}} {\left( {\frac{a}{x}} \right) ^k}\), where \({N_t} \in \left\{ {1, \ldots ,\infty } \right\} \). Then, \(\psi \) can be calculated as [44]
Then, we have new manipulation as:
Similarly, with help \({P_{input}} = \frac{{{P_S}{{\left| {{h_1}} \right| }^2}}}{{d_1^m}}\), (19) and (20), \(L_2\) can be expressed as
It is noted that equation (53) is rewritten by
where \({E^{HD}} = \frac{{\xi _d\gamma _{th2}^{HD}}}{{a{P_{{\mathrm{max}}}}}}\). Furthermore, equation (54) can be formulated as
Finally, we have outage probability for the cell-edge user.
It completes the proof.
Rights and permissions
About this article
Cite this article
Do, DT., Le, CB. & Le, AT. Joint of full-duplex relay, non-linear energy harvesting and multiple access in performance improvement of cell-edge user in heterogeneous networks. Wireless Netw 26, 6253–6266 (2020). https://doi.org/10.1007/s11276-020-02436-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-020-02436-7