Full-duplex overlay cognitive wireless powered communication network using RF energy harvesting

Abstract

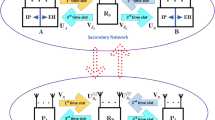
In this paper, a novel full-duplex overlay cognitive wireless powered communication network (FD-OCWPCN) is proposed where a full-duplex (FD) hybrid-access point (H-AP) supports the full access of all battery-free secondary users (SUs). The H-AP broadcasts wireless power to empower the nearby SUs in the downlink (DL) phase while decoding the information transmitted uplink (UL) phase by the SUs, simultaneously. To overcome the self-interference (SI) phenomenon in FD-OCWPCN, the problem of maximizing the system sum-throughput with optimal UL-DL transmission/reception time and H-AP’s transmit power allocation is considered. This problem is non-convex under perfect/imperfect SI cancelation (SIC), so we employ the active interference temperature control and the gradient projection techniques to effectively reduce it into a convex problem. Closed-form expressions for the perfect/imperfect SIC cases are also derived. To assess the performance of the FD-OCWPCN, a comparison with a half-duplex OCWPCN (HD-OCWPCN) is provided. The achievable average sum-throughput for different FD/HD-OCWPCN is compared in the context of the average and peak transmit power at the H-AP, the number of SUs, path loss exponent and fairness metric. The simulation results depict the superiority of the FD-OCWPCN over the HD-OCWPCN for the perfect SIC and the effective imperfect SIC.

Appendices

Appendix A

1.1 Proof of Proposition 2

Proposition 2 is proved by contradiction. First, we solve the problem of optimal allocation time, i.e., ${\varvec{\tau}}^{*} = \left[ {\tau_{0}^{*} , \tau_{1}^{*} , \ldots , \tau_{K}^{*} } \right]$. Assume that $\tilde{\user2{\tau }} = \left[ {\widetilde{{\tau_{0} }},\widetilde{{\tau_{1} }}, \ldots , \widetilde{{\tau_{K} }}} \right]$ are the optimal time solutions of (P4) which satisfy the constraint $\mathop \sum \limits_{i = 0}^{K} \widetilde{{\tau_{i} }} < 1$. Therefore $\widetilde{{\tau_{0} }} < 1 - \mathop \sum \limits_{i = 1}^{K} \widetilde{{\tau_{i} }}$. On the other hand, considering any value of ${\varvec{E}}_{h} \ge \bf 0$, it can be easily proved that the objective function (P4) is a monotonically increasing function of $\tau_{0}$, because

$$\frac{\partial }{\partial {\tau }_{0}}\left(\sum_{i=1}^{K}{\tau }_{i}{\mathit{log}}_{2}\left(1+\frac{1}{{\tau }_{i}}\frac{{\alpha }_{i}\sum_{\begin{array}{c}j=0\\ j\ne i\end{array}}^{K}{E}_{h,j}+{\beta }_{i}\sum_{\begin{array}{c}j=0\\ j\ne i\end{array}}^{K}{\tau }_{j}}{{\sigma }_{h}^{2}}\right)\right)=\frac{1}{{\mathrm{ln}(2)\sigma }_{h}^{2}} \sum_{i=1}^{K}\frac{{\beta }_{i}}{1+\frac{1}{{\tau }_{i}}\frac{{\alpha }_{i}\sum_{\begin{array}{c}j=0\\ j\ne i\end{array}}^{K}{E}_{h,j}+{\beta }_{i}\sum_{\begin{array}{c}j=0\\ j\ne i\end{array}}^{K}{\tau }_{j}}{{\sigma }_{h}^{2}}} \ge 0,$$

(A.1)

with $\left[ {1 - \mathop \sum \limits_{i = 1}^{K} \widetilde{{\tau_{i} }},\widetilde{{\tau_{1} }}, \ldots , \widetilde{{\tau_{K} }} } \right]$, the value of the objective function (P4) is always greater than $\bf\tilde{\user2{ \tau }}$. This contradicts our assumption, so the condition $\mathop \sum \limits_{i = 0}^{K} \tau_{i}^{*} = 1$ must always be satisfied to find the optimal time solutions.

Similarly, we can use the same approach to find the optimal energy solutions, i.e., ${\varvec E}_{h}^{*} = \left[ {E_{h,0}^{*} , E_{h,1}^{*} , \ldots , E_{h,K}^{*} } \right]$. It is assumed that $\widetilde{{{\varvec{E}}_{h} }} = \left[ {\widetilde{{E_{h,0} }},\widetilde{{E_{h,1} }}, \ldots , \widetilde{{E_{h,K} }}} \right]$ are the optimal energy solutions of (P4) and they meet the constraint $\mathop \sum \limits_{i = 0}^{K} \widetilde{{E_{h,i} }} < P_{avg}$, so $\widetilde{{E_{h,0} }} < P_{avg} - \mathop \sum \limits_{i = 1}^{K} \widetilde{{E_{h,i} }}$. On the other hand, given every ${\varvec{\tau}} \ge 0$, the objective function of (P4) is a monotonically increasing function of $E_{h,0}$, because

$$\frac{\partial }{{\partial E_{h,0} }}\left( {\mathop \sum \limits_{i = 1}^{K} \tau_{i} \log_{2} \left( {1 + \frac{1}{{\tau_{i} }}\frac{{\alpha_{i} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 0} \\ {j \ne i} \\ \end{array} }}^{K} E_{h,j} + \beta_{i} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 0} \\ {j \ne i} \\ \end{array} }}^{K} \tau_{j} }}{{\sigma_{h}^{2} }}} \right)} \right) = \frac{1}{{{\text{ln}}\left( 2 \right)\sigma_{h}^{2} }} \mathop \sum \limits_{i = 1}^{K} \frac{{\alpha_{i} }}{{1 + \frac{1}{{\tau_{i} }}\frac{{\alpha_{i} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 0} \\ {j \ne i} \\ \end{array} }}^{K} E_{h,j} + \beta_{i} \mathop \sum \nolimits_{{\begin{array}{*{20}c} {j = 0} \\ {j \ne i} \\ \end{array} }}^{K} \tau_{j} }}{{\sigma_{h}^{2} }}}} \ge 0.$$

(A.2)

The value of the objective function (P4) under the vector $\left[ {1 - \mathop \sum \limits_{i = 0}^{K} \widetilde{{E_{h,i} }},\widetilde{{E_{h,1} }}, \ldots , \widetilde{{E_{h,K} }} } \right]$ is always greater than $\widetilde{{{\varvec{E}}_{h} }}$. This contradicts our assumptions and the proof of Proposition 2 is done.

Appendix B

2.1 Proof of Proposition 3

$\hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right)$, $i = 1, 2, \ldots , K,$ denotes a jointly concave function of ${\varvec{E}}_{h}$ and ${\varvec{\tau}}$ if [30]

$${\hat{\mathbf{V}}}^{T} { }\nabla^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right){ }{\hat{\mathbf{V}}} \le 0,$$

(B.1)

where ${\hat{\mathbf{V}}} \in {\mathbb{R}}^{{2\left( {K + 1} \right) \times 1}}$ is an arbitrary real vector. Also, the Hessian for $\hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right)$ is defined as follows:

$${\nabla }^{2}{\widehat{R}}_{i}^{SN-FD-NoSI}\left({\tau }_{i},{E}_{h,i}\right)=\left[\begin{array}{cc}\widehat{\mathbf{A}}& \widehat{\mathbf{B}}\\ {\widehat{\mathbf{B}}}^{\mathrm{T}}& \widehat{\mathbf{C}}\end{array}\right],$$

(B.2)

where ${\hat{\mathbf{A}}}$, ${\hat{\mathbf{B}}}$, and ${\hat{\mathbf{C}}}$ are:

$$\left[ {{\hat{\mathbf{A}}}} \right]_{j,k} = \frac{{\partial^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right)}}{{\partial \tau_{j} \partial \tau_{k} }} = \left\{ {\begin{array}{*{20}c} { - \frac{1}{ln2}\left( {\frac{{\mho_{i}^{2} }}{{\tau_{i} \left( {1 + {\Omega }_{i} } \right)^{2} }}} \right),} & {j = k = i.} \\ {0,} & {{\text{otherwise}}.} \\ \end{array} } \right.$$

(B.3)

$$\left[ {{\hat{\mathbf{B}}}} \right]_{j,k} = \frac{{\partial^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right)}}{{\partial \tau_{j} \partial E_{h,k} }} = \left\{ {\begin{array}{*{20}c} { - \frac{1}{ln2}\left( {\frac{{\mho_{i} \left( {\alpha_{i} /\sigma_{h}^{2} } \right)}}{{\tau_{i} \left( {1 + {\Omega }_{i} } \right)^{2} }}} \right),} & {j = k = i.} \\ {0,} & {{\text{otherwise}}.} \\ \end{array} } \right.$$

(B.4)

$$\left[ {{\hat{\mathbf{C}}}} \right]_{j,k} = \frac{{\partial^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right)}}{{\partial E_{h,j} \partial E_{h,k} }} = \left\{ {\begin{array}{*{20}c} { - \frac{1}{ln2}\left( {\frac{{\left( {\alpha_{i} /\sigma_{h}^{2} } \right)^{2} }}{{\tau_{i} \left( {1 + {\Omega }_{i} } \right)^{2} }}} \right),} & {j = k = i.} \\ {0,} & {{\text{otherwise}}.} \\ \end{array} } \right.$$

(B.5)

where $\left[ {\mathbf{X}} \right]_{j,k}$ is the element of matrix ${\mathbf{X}}$. In addition, ${\Omega }_{i} = \left( {\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)} \right)/\left( {\tau_{i} \sigma_{h}^{2} } \right)$ and $\mho_{i} = \left( {\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} } \right)/\left( {\tau_{i} \sigma_{h}^{2} } \right)$. Define ${\hat{\mathbf{V}}} = \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{V}}}_{1}^{T} } & {{\hat{\mathbf{V}}}_{2}^{T} } \\ \end{array} } \right]^{T}$, where ${\hat{\mathbf{V}}}_{1} = \left[ {\begin{array}{*{20}c} {\hat{v}_{10} } & {\hat{v}_{11} } & \ldots & {\hat{v}_{1K} } \\ \end{array} } \right]^{T}$ and ${\hat{\mathbf{V}}}_{2} = \left[ {\begin{array}{*{20}c} {\hat{v}_{20} } & {\hat{v}_{21} } & \ldots & {\hat{v}_{2K} } \\ \end{array} } \right]^{T}$are two arbitrary vectors. Since ${\hat{\mathbf{V}}}_{1}^{T} {\mathbf{\hat{B}\hat{V}}}_{2} = {\hat{\mathbf{V}}}_{2}^{T} {\hat{\mathbf{B}}}^{T} {\hat{\mathbf{V}}}_{1}$, ${\hat{\mathbf{B}}}$ shows a symmetric matrix. According to Eqs. (B.3)-(B.5) for ${\hat{\mathbf{V}}}^{T} { }\nabla^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right){ }{\hat{\mathbf{V}}}$, we have:

$${\hat{\mathbf{V}}}^{T} { }\nabla^{2} \hat{R}_{i}^{SN - FD - NoSI} \left( {\tau_{i} ,E_{h,i} } \right){ }{\hat{\mathbf{V}}} = { }{\hat{\mathbf{V}}}_{1}^{T} {\hat{\mathbf{A}}}{ }{\hat{\mathbf{V}}}_{1} + 2{ }{\hat{\mathbf{V}}}_{2}^{T} {\hat{\mathbf{B}}}{ }{\hat{\mathbf{V}}}_{1} + { }{\hat{\mathbf{V}}}_{2}^{T} {\hat{\mathbf{C}}}{ }{\hat{\mathbf{V}}}_{2} = - \frac{1}{{ \tau_{i} \left( {1 + {\Omega }_{i} } \right)^{2} ln2}}\left( {\mho_{i} \hat{v}_{1i} + \left( { \alpha_{i} /\sigma_{h}^{2} } \right)\hat{v}_{2i} } \right)^{2} \le 0.$$

(B.6)

Thus, Proposition 3 is proved.

Appendix C

3.1 Proof of Proposition 4

From Lemma 3.2 in [11], the objective function of (P5) is a monotonically increasing function of $\tau_{i} , E_{h,i} ,{ } i = 1, 2, \ldots , K.$ So, the optimal time in dedicated energy time slot ($\tau_{0}^{*}$) and the optimal transmitted energy in the time slot of the dedicated energy ($E_{h,0}^{*}$) are obtained as,

$$\tau_{0}^{*} = min\left( {\left[ {\frac{{\left( {R_{min} - r\left( {\Upsilon } \right)} \right)}}{{\left( {r\left( 0 \right) - r\left( {\Upsilon } \right)} \right)}}} \right]^{ + } , E_{h,0}^{*} /P_{peak} ,1} \right), { E_{h,0}^{*} = P_{peak} \tau_{0}^{*} }.$$

(C.1)

where $\left( {\mathcal{t}} \right)^{ + } \triangleq max\left( {0,\mathcal{t} } \right)$. Therefore, (P5) is simplified to the following problem:

$$\begin{aligned}& \left( {P5 - 1} \right): \mathop {maximize}\limits_{{\user2{\tau^{\prime}} \ge {\bf 0},{\varvec{E}}_{h}^{^{\prime}} \ge {\bf 0}}} \mathop \sum \limits_{i = 1}^{K} \tau_{i} \log_{2} \left( {1 + \frac{1}{{\tau_{i} }}\frac{{\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)}}{{\sigma_{h}^{2} }}} \right)\\ & {\text{subject to}}:\end{aligned}$$

(C.2)

• (a) $\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right) \le \gamma_{i} \left( {\Upsilon } \right)\tau_{i} { }, i = 1, 2, \ldots , K,$

• (b) $\mathop \sum \limits_{i = 1}^{K} E_{h,i} = P_{avg} - E_{h,0}^{*}$,

• (c) $\mathop \sum \limits_{i = 1}^{K} \tau_{i} = 1 - \tau_{0}^{*} ,$

• (d) $E_{h,i} - P_{peak} \tau_{i} \le 0, i = 1, 2, \ldots , K,$

  $${\text{(e) }} 0 \le \tau_{i} \le 1, E_{h,i} \ge 0, i = 1, 2, \ldots , K.$$

where $\user2{\bf \tau^{\prime}} = \left[ {{ }\tau_{1} ,{ } \ldots ,{ }\tau_{K} } \right]$ and ${\varvec{E}}_{h}^{^{\prime}} = \left[ {{ }E_{h,1} ,{ } \ldots ,{ }E_{h,K} } \right].$ Given that (P5-1) is a convex optimization problem and satisfies the Slater condition [30], the duality gap between the problem and its dual must be zero. Now, we solve the dual problem of (P5-1). The partial Lagrangian function of (P5-1) with respect to constraints (a, b and c) is expressed as:

$${\mathcal{L}}\left( {\user2{\bf{\tau}^{\prime}},{\varvec{E}}_{h}^{^{\prime}} ,{\varvec{\lambda}},\mu ,\nu } \right) = \hat{R}_{sum}^{SN - FD - NoSI} \left( {\user2{\bf{\tau}^{\prime}}} \right) - \mathop \sum \limits_{i = 1}^{K} \lambda_{i} \left( {\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right) - \gamma_{i} \left( {\Upsilon } \right)\tau_{i} } \right)$$

$$+ \mu \left( {\mathop \sum \limits_{i = 1}^{K} E_{h,i} - (P_{avg} - E_{h,0}^{*} )} \right) + \nu \left( {\mathop \sum \limits_{i = 1}^{K} \tau_{i} - \left( {1 - \tau_{0}^{*} } \right)} \right),$$

(C.3)

where, $\hat{R}_{sum}^{SN - FD - NoSI} \left( {\user2{\bf{\tau}^{\prime}}} \right) = \mathop \sum \limits_{i = 1}^{K} \tau_{i} \log_{2} \left( {1 + \frac{1}{{\tau_{i} }}\frac{{\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)}}{{\sigma_{h}^{2} }}} \right){ }$ and ${\varvec{\lambda}} = \left[ {\lambda_{1} ,\lambda_{2} ,{ } \ldots ,{ }\lambda_{K} } \right] \ge \bf{0}$ is a non-negative vector of the Lagrange multipliers associated with the constraints in (a) of (P5-1). The parameters $\mu$ and $\nu$ are also the assigned Lagrangian dual variables to the total energy and time allocation constraints during a block time, according to the constraints (b) and (c) of (P5-1). Then the dual function of (P5-1) is expressed as ${\mathcal{G}}\left( {{\varvec{\lambda}},\mu ,\nu } \right) = \mathop {\max }\limits_{{\left( {\user2{\bf{\tau}^{\prime}},{\varvec{E}}_{h}^{^{\prime}} } \right) \in {\mathcal{D}}}} \left( {{\mathcal{L}}\left( {\user2{\bf{\tau}^{\prime}},{\varvec{E}}_{h}^{^{\prime}} ,{\varvec{\lambda}},\mu ,\nu } \right)} \right),$where ${\mathcal{D}}$ is a realizable set of $\left( {\user2{\bf{\tau}^{\prime}},{\varvec{E}}_{h}^{^{\prime}} } \right)$ with respect to the constraints (d) and (e) of (P5-1). The dual problem of (P5-1) is thus given by $\mathop {\min }\limits_{{{\varvec{\lambda}},\mu ,\nu }} {\mathcal{G}}\left( {{\varvec{\lambda}},\mu ,\nu } \right).$ The Lagrangian function of (C.3) is:

$${\mathcal{L}}\left( {\user2{\tau^{\prime}},{\varvec{E}}_{h} ,{\varvec{\lambda}}} \right) = \mathop \sum \limits_{i = 1}^{K} {\mathcal{L}}_{i} \left( {\tau_{i} , E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right) - \lambda_{i} \left( {\alpha_{i} P_{avg} + \beta_{i} } \right) - \mu (P_{avg} - E_{h,0}^{*} ) - \nu \left( {1 - \tau_{0}^{*} } \right),$$

(C.4)

where ${\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right) = \hat{R}_{i}^{SN - FD - NoSI} \left( {\user2{\bf{\tau}^{\prime}}} \right) + \left( {\lambda_{i} \alpha_{i} + \mu } \right)E_{h,i} + \left( {\lambda_{i} \left( {\beta_{i} + \gamma_{i} \left( {\Upsilon } \right)} \right) + \nu } \right)\tau_{i}$. To maximize the Lagrangian function at ${\mathcal{G}}\left( {{\varvec{\lambda}},\mu ,\nu } \right)$, we must maximize each of ${\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)$ with respect to the constraints (d) and (e) of (P5-1). Because the function ${\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)$ with $\lambda_{i}$, $\mu$ and $\nu$ depends only on $\tau_{i}$ and $E_{h,i}$. Therefore, we can solve the following sub-problem:

$$\begin{aligned}& \left( {P5 - 2} \right): \mathop {maximize}\limits_{{\tau_{i} , E_{h,i} }} {\mathcal{L}}_{i} \left( {\tau_{i} , E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)\\ & {\text{subject to}}:\end{aligned}$$

(C.5)

(a) $E_{h,i} \le P_{peak} \tau_{i} , i = 1, 2, \ldots , K,$

$$ {\text{(b) }}0 \le \tau_{i} \le 1, E_{h,i} \ge 0, i = 1, 2, \ldots ,K.$$

To solve (P5-2) when $\lambda_{i}$, $\mu$ and $\nu$ are available, we can obtain $E_{h,i}$ with $\tau_{i}$ and vice versa $\tau_{i}$ with $E_{h,i}$. For this purpose, first we compute the partial derivation of ${\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)$ for $E_{h,i}$ with given $\lambda_{i}$, $\mu$, $\nu$ and $\tau_{i}$. By letting $\partial {\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)/\partial E_{h,i} = 0,$ we have:

$$\frac{{\alpha_{i} /\sigma_{h}^{2} }}{{1 + \left( {\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)} \right)/\left( {\tau_{i} \sigma_{h}^{2} } \right)}} = \left( {\lambda_{i} \alpha_{i} + \mu } \right)ln2.$$

(C.6)

Note that $0 \le E_{h,i} \le P_{peak} \tau_{i}$ lies in the feasible region ${\mathcal{D}}$ due to the constraints (d) and (e) of (P5-1). Therefore, according to (C.6), $E_{h,i}$ is obtained as follows:

$$E_{h,i} = min\left[ {\left( {P_{avg} + \frac{{\tau_{i} \sigma_{h}^{2} }}{{\alpha_{i} }} + \frac{{\beta_{i} \left( {1 - \tau_{i} } \right)}}{{\alpha_{i} }} - \frac{{\tau_{i} }}{{\left( {\lambda_{i} \alpha_{i} + \mu } \right)ln2}}} \right)^{ + } , P_{peak} \tau_{i} } \right], i = 1, 2, \ldots ,K.$$

(C.7)

The left-hand side of (C.6) is always positive, so, $\mu > \mathop {\max }\limits_{{i = 1,{ }2,{ } \ldots ,K}} \left( { - \lambda_{i} \alpha_{i} } \right).{ }$ Secondly, for $E_{h,i}$, we obtain a partial derivation of ${\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)$ with respect to $\tau_{i}$ with given $\lambda_{i}$, $\mu$, $\nu$. Hence $\partial {\mathcal{L}}_{i} \left( {\tau_{i} ,{ }E_{h,i} ,\lambda_{i} ,\mu ,\nu } \right)/\partial \tau_{i} = 0,$ is:

$$\ln \left( {1 + \mathcal{z}_{i} } \right) - \frac{{\mathcal{z}_{i} }}{{1 + \mathcal{z}_{i} }} - \frac{{\beta_{i} /\sigma_{h}^{2} }}{{1 + \mathcal{z}_{i} }} = - \left( {\lambda_{i} \left( {\beta_{i} + \gamma_{i} \left( {\Upsilon } \right)} \right) + \nu } \right)ln2,$$

(C.8)

where $\mathcal{z}_{i} = \frac{{\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)}}{{\tau_{i} \sigma_{h}^{2} }} \ge 0, i = 1, 2, \ldots ,K.$ Assuming the left-hand side of (C.8) equals $h\left( {\mathcal{z}_{i} } \right)$, it is straightforward to show that $h\left( {\mathcal{z}_{i} } \right)$ is a monotonically increasing function of $\mathcal{z}_{i}$, because $\partial h\left( {\mathcal{z}_{i} } \right)/\partial \mathcal{z}_{i} = \left( {\mathcal{z}_{i} + \beta_{i} /\sigma_{h}^{2} } \right)/\left( {1 + \mathcal{z}_{i} } \right)^{2} \ge 0$. Therefore, since $\mathcal{z}_{i}$’s are non-negative, then the minimum value of $h\left( {\mathcal{z}_{i} } \right)$ is equal to $- \beta_{i} /\sigma_{h}^{2}$, which is obtained for $\mathcal{z}_{i} = 0$. If $- \beta_{i} /\sigma_{h}^{2} > - \left( {\lambda_{i} \left( {\beta_{i} + \gamma_{i} \left( {\Upsilon } \right)} \right) + \nu } \right)ln2$, then $\mathcal{z}_{i}^{*}$ does not exist to solve (C.8). In addition, if $- \beta_{i} /\sigma_{h}^{2} \le - \left( {\lambda_{i} \left( {\beta_{i} + \gamma_{i} \left( {\Upsilon } \right)} \right) + \nu } \right)ln2 < 0$, we can find $\mathcal{z}_{i}^{*}$ to solve (C.8) and obtain non-zero $\tau_{i}$. So, $\nu \le \mathop {\min }\limits_{{i = 1,2{ } \ldots ,K}} \left( {\frac{{\beta_{i} }}{{\sigma_{h}^{2} ln2}} - \lambda_{i} \left( {\beta_{i} + \gamma_{i} \left( {\Upsilon } \right)} \right)} \right)$. Since $0 \le E_{h,i} /P_{peak} \le \tau_{i}$ is in the feasible region ${\mathcal{D}}$, so as soon as $\mathcal{z}_{i}^{*}$ is calculated from the solution (C.8), $\tau_{i}$ is achieved as follows:

$$\tau_{i} = max\left[ {\left( {\frac{{\left( {\alpha_{i} \left( {P_{avg} - E_{h,i} } \right) + \beta_{i} } \right)}}{{\left( {\mathcal{z}_{i} \sigma_{h}^{2} + \beta_{i} } \right)}}} \right)^{ + } , E_{h,i} /P_{peak} } \right],$$

(C.9)

and the proof of Proposition 4 is attained.

Appendix D

4.1 Proof of Proposition 5

According to the proof of Proposition 3, we must show that the Hessian matrix of $\hat{R}_{i}^{SN - FD} \left( {\tau_{i} ,{ }p_{h,i}^{{\left( {l - 1} \right)}} } \right)$, $\forall i \in \left\{ {1,{ }2,{ } \ldots ,{ }K} \right\}$, is non-positive. The Hessian matrix for $\hat{R}_{i}^{SN - FD} \left( {\tau_{i} ,{ }p_{h,i}^{{\left( {l - 1} \right)}} } \right){ }$ is defined as $\left[ {\hat{d}_{j,k}^{\left( i \right)} } \right]$, where $\hat{d}_{j,k}^{\left( i \right)}$ denotes the element of ${ }\nabla^{2} \hat{R}_{i}^{SN - FD} \left( {\tau_{i} ,{ }p_{h,i}^{{\left( {l - 1} \right)}} } \right)$. Therefore,

$$\hat{d}_{j,k}^{\left( i \right)} = \left\{ {\begin{array}{*{20}c} { - \frac{1}{ln2}\left( {\frac{{\left( {\hat{\mho }_{i} } \right)^{2} }}{{\tau_{i} \left( {1 + {\hat{\Omega }}_{i} } \right)^{2} }}} \right),} & {j = k = i,} \\ {0,} & {otherwise,} \\ \end{array} } \right.$$

(D.1)

where ${\hat{\Omega }}_{i} = \frac{{\left( {\alpha_{i} \left( {P_{avg} - \tau_{i} p_{h,i}^{{\left( {l - 1} \right)}} } \right) + \beta_{i} \left( {1 - \tau_{i} } \right)} \right)}}{{\tau_{i} \left( {\omega p_{h,i}^{{\left( {l - 1} \right)}} + \sigma_{h}^{2} } \right)}}$and $\hat{\mho }_{i} = \frac{{\left( {\alpha_{i} P_{avg} + \beta_{i} } \right)}}{{\tau_{i} \left( {\omega p_{h,i}^{{\left( {l - 1} \right)}} + \sigma_{h}^{2} } \right)}}$. For any arbitrary vector ${\mathbf{V}} = \left[ {\begin{array}{*{20}c} {v_{0} } & {v_{1} } & \ldots & {v_{K} } \\ \end{array} } \right]^{T}$ and also $\tau_{i} \ge 0$, it is deduced ${\mathbf{V}}^{T} { }\nabla^{2} \hat{R}_{i}^{SN - FD} \left( {\tau_{i} ,{ }p_{h,i}^{{\left( {l - 1} \right)}} } \right){ }{\mathbf{V}} \le 0$.