Abstract
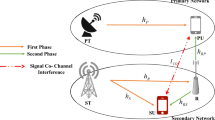
This article studies the interweave cognitive network with non-orthogonal multiple access (NOMA) principle under the appearance of one eavesdropper. The best relay selection method is used by considering two users of main channels at the same time. The general accuracy and asymptotic theory expressions of the system performance for two NOMA cognitive secondary users, e.g., outage probability and interception probability are derived, and they are also verified through Monte Carlo simulation. On this basis, we also investigate the effects of important system parameters such as the relay number, outdated channel side information (CSI), imperfect spectrum sensing, NOMA power allocation and imperfect successive interference cancellation (SIC) factor. It can be concluded that the outage diversity order for the NOMA users in the main channels can achieve as the relay number K when the perfect CSI appears. But the outage diversity order decreases to only one when the outdated CSI appears. However the intercept probability of the wiretap channel only got the diversity order as zero regardless of relay. And the imperfect spectrum sensing, imperfect SIC and NOMA power allocation can not affect the diversity order although they affect the system performance.










Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no data-sets were generated or analysed during the current study.
Code availability
Code will be made available on request.
References
Wang, P., Xiao, J., & Li, P. (2006). Comparison of orthogonal and non-orthogonal approaches to future wireless cellular systems. IEEE Vehicular Technology Magazine, 1(3), 4–11.
Saito, Y., Benjebbour, A., Kishiyama, Y., & Nakamura, T. (2013). System-level performance evaluation of downlink non-orthogonal multiple access (NOMA). In 2013 IEEE 24th Annual international symposium on personal, indoor, and mobile radio communications (PIMRC). pp. 611–615.
Dai, L., Wang, B., Yuan, Y., Han, S., Chih-Lin, I., & Wang, Z. (2015). Non-orthogonal multiple access for 5g: solutions, challenges, opportunities, and future research trends. IEEE Communications Magazine, 53(9), 74–81.
Andrews, J. G. (2005). Interference cancellation for cellular systems: A contemporary overview. IEEE Wireless Communications Magazine, 12(2), 19–29.
Ding, Z., Yang, Z., Fan, P., & Poor, H. V. (2014). On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Processing Letters, 21(12), 1501–1505.
Ding, Z., Peng, M., & Poor, H. V. (2015). Cooperative non-orthogonal multiple access in 5G systems. IEEE Communications Letters, 19(8), 1462–1465.
Li, X., Li, J., Liu, Y., Ding, Z., & Nallanathan, A. (2020). Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Transactions on Wireless Communications, 19(1), 680–695.
Le, T. A., & Kong, H. Y. (2020). Performance analysis of downlink nomaCEH relaying network in the presence of residual transmit rf hardware impairments. Wireless Networks, 26, 1045–1055.
Zhong, B., & Zhang, Z. (2018). Opportunistic two-way full-duplex relay selection in underlay cognitive networks. IEEE Systems Journal, 12(1), 725–734.
Li, Q., & Varshney, P. K. (2017). Resource allocation and outage analysis for an adaptive cognitive two-way relay network. IEEE Transactions on Communications, 16(7), 4727–4737.
Le, L. B., & Hossain, E. (2008). Resource allocation for spectrum underlay in cognitive radio networks. IEEE Transactions on Wireless Communications, 7(12), 5306–5315.
Wang, X., Li, E., Ha, D. B., Hoang, T., & Zhang, H. (2016). Secure cognitive relay network: Joint the impact of imperfect spectrum sensing and outdated feedback. Wireless Personal Communications, 87, 165–192.
Lv, L., Chen, J., Ni, Q., Ding, Z., & Jiang, H. (2018). Cognitive non-orthogonal multiple access with cooperative relaying: a new wireless frontier for 5G spectrum sharing. IEEE Communications Magazine, 56(4), 188–195.
Wang, Y., Wu, Y., Zhou, F., Wu, Y., & Wang, Y. (2017). Multi-objective resource allocation in NOMA cognitive radios based on a practical non-linear energy harvesting model. In: 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), pp. 1–6.
Lv, L., Ding, Z., Ni, Q., & Chen, J. (2018). Secure MISO-NOMA transmission with artificial noise. IEEE Transactions on Vehicular Technology, 67(7), 6700–6705.
Zhao, N., Li, D., Liu, M., Cao, Y., & Wang, X. (2019). Secure transmission via joint precoding optimization for downlink MISO NOMA. IEEE Transactions on Vehicular Technology, 68(8), 7603–7615.
Zhao, N., Wang, W., Wang, J., Chen, Y., Lin, Y., & Ding, Z. (2019). Joint beamforming and jamming optimization for secure transmission in MISO-NOMA networks. IEEE Transactions on Communications, 67(3), 2294–2305.
Li, X., Zhao, M., Zeng, M., Mumtaz, S., Menon, V., Ding, Z., & Dobre, O. (2021). Hardware impaired ambient backscatter NOMA system: Reliability and security. IEEE Transactions on Communications, 69(4), 2723–2736.
Li, X., Wang, Q., Zeng, M., Liu, Y., Dang, S., Tsiftsis, T., & Dobre, O. (2023). Physical-layer authentication for ambient backscatter aided NOMA symbiotic systems. IEEE Transactions on Communications, 71(4), 2288–2303.
Shu, Z., & Qian, Y. (2013). On physical layer security for cognitive radio networks. IEEE Network, 27(3), 28–33.
Zhu, J. (2013). Security-reliability trade-off for cognitive radio networks in the presence of eavesdropping attack. Eurasip Journal on Advances in Signal Processing, 2013(1), 1–10.
Shang, Z., Zhang, T., Tao, L., Xiang, Z., & Yang, W. (2021). Physical layer security in cognitive noma sensor networks with full-duplex technique. International Journal of Distributed Sensor Networks, 17(12), 331–342.
Xiang, Z., Yang, W., Pan, G., Cai, Y., & Song, Y. (2019). Physical layer security in cognitive radio inspired noma network. IEEE Journal of Selected Topics in Signal Processing, 17(3), 700–714.
Li, X., Zhao, M., Gao, X. C., Li, L., Do, D. T., Rabie, K. M., et al. (2020). Physical layer security of cooperative noma for IoT networks under I/Q imbalance. IEEE Access, 8, 51189–51199.
Tang, S., & Chen, L. (2022). Computational intelligence and deep learning for next generation edge-enabled industrial IoT. IEEE Transactions Network Science Engineering, 10(5), 2881–2893.
Chen, H., Liu, J., Dong, Z., Zhou, Y., & Guo, W. (2011). Exact capacity analysis of partial relay selection under outdated csi over rayleigh fading channels. IEEE Transactions on Vehicular Technology, 60(8), 4014–4018.
Zou, Y., Champagne, B., Zhu, W. P., & Hanzo, L. (2014). Relay-selection improves the security-reliability trade-off in cognitive radio systems. IEEE Transactions on Communications, 63(1), 215–228.
Wang, X., Li, E., & Yang, G. (2021). Performance analysis of 5G downlink cooperative NOMA network with multi-antenna relay. Physical Communication, 52(101586), 1–10.
Liu, C., Fu, X., Wang, Y., Guo, L., Liu, Y., Lin, Y., Zhao, H., & Gui, G. (2024). Overcoming data limitations: a few-shot specific emitter identification method using self-supervised learning and adversarial augmentation. IEEE Transactions Information. Forensics Security, 19, 500–513.
Lin, Y., Tu, Y., Dou, Z., Chen, L., & Mao, S. (2020). Contour stella image and deep learning for signal recognition in the physical layer. IEEE Transactions on Cognitive Communications and Networking, 7(1), 34–46.
Yao, Z., Fu, X., Guo, L., Wang, Y., Lin, Y., Shi, S., & Gui, G. (2023). Few-shot specific emitter identification using asymmetric masked auto-encoder. IEEE Communications Letters, 27(10), 2657–2661.
Tang, S., Xia, J., Fan, L., Lei, X., Xu, W., & Nallanathan, A. (2022). Dilated convolution based CSI feedback compression for massive MIMO systems. IEEE Transcations Vehicular Technology, 71(10), 11216–11221.
He, L., Fan, L., Lei, X., Tang, X., Fan, P., & Nallanathan, A. (2023). Learning-based MIMO detection with dynamic spatial modulation. In IEEE Transactions on cognitive communications and networking, early access, pp. 1–12.
Funding
This work was supported by Shandong Provincial Natural Science Foundation (ZR2020MF001, ZR2022MF273), A Project of Shandong Province Higher Educational Science and Technology Program (J18KA315), the National Defense Science and Technology Innovation Zone of China - Marine Science and Technology Collaborative Innovation Center Foundation of Qingdao (22-05-CXZX-04-02-06).
Author information
Authors and Affiliations
Contributions
Xinjie Wang proposed the idea, checked the derivations, revised the paper. Min Zhang derived the equations, done the simulations, wrote the draft. Enyu Li and Guang Yang revised the paper. Xuhu Wang given some suggestions for simulations.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
\(I_{1}\) and \(I_{2}\) in (20) can be given as
\(I_{3}^{k}=Pr\{{\left| {D}\right| =k}\vert {H=H_{0},\tilde{H}=H_{0}}\}\) represents the probability of successful relay decoding set under the condition that S detects the spectrum idle and matches the actual situation, and it means \(\alpha _{p}=0\). \(I_{4}^{k}=Pr\{{\left| {D}\right| =k}\vert {H=H_{1},\tilde{H}=H_{0}}\}\) is the probability of successful relay decoding if the sensing result does not match the actual situation, so it leads to \(\alpha _{p}=1\). \(I_{3}^{k}\) and \(I_{4}^{k}\) also mean that there are \(k(k=0,1,2,...,K)\) relay decodes successfully. Substitute (3) and (4) into \(I_{3}^{k}\) and \(I_{4}^{k}\),we have (33) and (34) as follows.
Based on (17), \(I_{6}\) can be expressed as
Substituting (31), (32), (33), (34) and (35) into (20), we get (21).
Appendix B
When considering the wiretap of the eavesdropper, the number of decoding relays should be larger than zero, so \(I_{3}^{k}=Pr\{{\left| {D}\right| =k}\vert {H=H_{0},\tilde{H}=H_{0}}\}\) can be represented as \(I_{3}^{k_{*}}=Pr\{{\left| {D}\right| =k,k>0}\vert {H=H_{0},\tilde{H}=H_{0}}\}\),where \(k>0\). So \(I_{3}^{k_{*}}\) can be expressed as
Similarly, we can also obtain \({I_{4}^{k_{*}}}\) as
Substitute (13) into \(Pr\{\gamma _{0,E_{i}}>\gamma _{thE_{i}}^{x_{i}}\}\) and \(Pr\{\gamma _{1,E_{i}}>\gamma _{thE_{i}}^{x_{i}}\}\), we have
Substitute (20), (21), (36), (37), (38) and (39) into (24), we have the intercept probability of \(x_{i}\) by E as (25).
Appendix C
In the high SNR region, \(I_{3}^{k}\) can be gotten with the help of (26) as
\(I_{4}^{k}\) can be expressed as
Based on (27), the asymptotic value of \(I_{6}\) can be expressed as \(I_{6}^{*}\). When \(\rho _{i}<1\), \(I_{6}^{*}\) is given as
Substituting (40), (41) and (42) into (21), the outage probability with \(\rho _{i}<1\) can be gotten as (28).
when \(\rho _{i}=1\), \(I_{6}^{*}\) can be expressed as
Substituting (40), (41) and (43) into (21), the outage probability with \(\rho _{i}=1\) can be gotten as (29).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, M., Wang, X., Li, E. et al. Secure 5G downlink NOMA cognitive relay network: joint the impact of imperfect spectrum sensing and outdated CSI. Wireless Netw 30, 1925–1937 (2024). https://doi.org/10.1007/s11276-023-03632-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11276-023-03632-x