Performance evaluation of multiple relay SWIPT enabled cooperative NOMA network in the presence of interference

Abstract

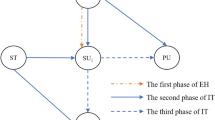
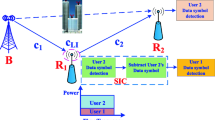
Simultaneous wireless information and power transmission (SWIPT) allows the use of RF signals for both information detection and energy harvesting. Integration of cooperation, NOMA and SWIPT can provide energy-efficient, reliable, and spectral-efficient networks. Therefore, this study aims to design energy harvesting-enabled cooperative NOMA (C-NOMA) networks. This work investigates relay selection for multiple relay downlink C-NOMA networks with SWIPT in the presence of interference. The analytical closed-form outage probability expressions for the proposed relay selection are derived. Subsequently, the impact of various parameters, including the number of available relay nodes, energy harvesting parameters, and energy conversion efficiency, is analyzed on the performance of proposed networks. The finding showed that system performance improves with the number of intermediate relaying nodes, transmit power, and energy conversion efficiency. Comparative analysis of NOMA and time division multiple access TDMA proved the superiority of NOMA over traditional OMA schemes.

Appendices

Appendix A

$${\text{P}}_{1} = \Pr \left( {X < C_{1} \left( {CX_{I} + 1} \right)} \right) + \Pr \left( {C_{1} \left( {CX_{I} + N_{0} } \right) > { }X{ } < \frac{1}{{\rho_{s} }}\left( {\frac{{C_{2} }}{{X_{1} }} - \rho_{I} X_{I} } \right){ }} \right),$$

(A.1)

Where $X={\left|{g}_{n}\right|}^{2},{X}_{1}={\left|{h}_{n1}\right|}^{2}, {X}_{I}=\sum_{i=1}^{L}{\left|{g}_{i}\right|}^{2}, C=\left(1-\xi \right){\rho }_{I} and {\rho }_{I}=\frac{{P}_{I}}{{N}_{0}}.$

$$P_{1} = \mathop \smallint \limits_{0}^{\infty } F_{X} (C_{1} \left( {CX_{I} + 1 } \right)) f_{{X_{I} }} \left( x \right) dx + \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } \left( {F_{X} \left( {\frac{1}{{\rho_{s} }}\left( {\frac{{C_{2} }}{{X_{1} }} - \rho_{I} X_{I} } \right)} \right) - F_{X} \left( {C_{1} \left( {CX_{I} + 1} \right)} \right)} \right) f_{{X_{1} ,X_{I} }} \left( {x,y} \right) dxdy$$

(A.2)

$$= \mathop \smallint \limits_{0}^{\infty } F_{X} (C_{1} \left( {CX_{I} + N_{0} } \right)) f_{{X_{I} }} \left( x \right) dx + \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } \left( {F_{X} \left( {\frac{1}{{\rho_{s} }}\left( {\frac{{C_{2} }}{{X_{1} }} - \rho_{I} X_{I} } \right)} \right)} \right) f_{{X_{2} ,X_{I } }} \left( {x,y} \right) dxdy - \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } \left( {F_{X} (C_{1} \left( {CX_{I} + N_{0} } \right)} \right) f_{{X_{!} ,X_{I } }} \left( {x,y} \right) dxdy$$

(A.3)

As ${X}_{1},{X}_{2} and {X}_{I}$ are independent of each other, first and last term cancels out.

$$={\int }_{0}^{\infty }{\int }_{0}^{\infty }\left({F}_{X}\left(\frac{1}{{\rho }_{s}}\left(\frac{{C}_{2}}{{X}_{1}}-{\rho }_{I}{X}_{I}\right)\right)\right) { f}_{{X}_{1},{X}_{I }}\left(x,y\right) dxdy$$

(A.4)

$$=\frac{{\lambda }_{I}^{L}{\lambda }_{1}}{\Gamma ({\text{L}})}{\int }_{0}^{\infty }{\int }_{0}^{\infty }{\left(1-{e}^{-\frac{{\lambda }_{g}}{{\rho }_{s}}\left(\frac{{C}_{2}}{x}-{\rho }_{I}y\right)}\right)}^{M}{{{ e}^{-{\lambda }_{1}x}y}^{L-1} e}^{-{\lambda }_{I}y} dxdy$$

(A.5)

Using binomial expansion to further solve the P₁

$$=1-\frac{{\lambda }_{I}^{L}{\lambda }_{1}}{\Gamma ({\text{L}})}\sum_{n=1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right) {\left(-1\right)}^{n+1}{\int }_{0}^{\infty }{\int }_{0}^{\infty }{e}^{-\frac{{n\lambda }_{g}}{{\rho }_{s}}\left(\frac{{C}_{2}}{x}-{\rho }_{I}y\right)}{{{ e}^{-{\lambda }_{1}x}y}^{L-1} e}^{-{\lambda }_{I}y} dxdy$$

(A.6)

$$=1-\frac{{\lambda }_{I}^{L}{\lambda }_{1}}{\Gamma ({\text{L}})}\sum_{n=1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right) {\left(-1\right)}^{n+1}{\int }_{0}^{\infty }{\int }_{0}^{\infty }{e}^{-\frac{{n\lambda }_{g}*{C}_{2}}{{\rho }_{s*x}}-{\lambda }_{1}x}*{{y}^{L-1} e}^{-y({\lambda }_{I}-\frac{n{\rho }_{I}{\lambda }_{g}}{{\rho }_{s}})} dxdy$$

(A.7)

${\int }_{0}^{\infty }{e}^{-\frac{\beta }{4x}-\lambda x}=\sqrt{\beta /\lambda } {K}_{1}\sqrt{\beta \lambda }$ is used to solve above equation further,

$$=1-\frac{{\lambda }_{I}^{L}{\lambda }_{1}}{\Gamma ({\text{L}})}\sum_{n=1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right) {\left(-1\right)}^{n+1}\sqrt{\frac{4n{C}_{2}{\lambda }_{g}}{{\rho }_{s}{\lambda }_{1}}} {K}_{1}\sqrt{\frac{4n{C}_{2}{\lambda }_{g}{\lambda }_{1}}{{\rho }_{s}}}{\int }_{0}^{\infty }{{y}^{L-1} e}^{-y({\lambda }_{I}-\frac{n{\rho }_{I}{\lambda }_{g}}{{\rho }_{s}})} dy$$

(A.8)

From (3.381.4) of (Gradshteyn & Ryzhik, 2014), $\underset{0}{\overset{\infty }{\int }}{x}^{v-1}{e}^{-\mu x}dx=\frac{1}{{\mu }^{v}}\Gamma (v)$

$$P_{1} = 1 - \lambda_{I}^{L} \lambda_{1} \mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {\lambda_{I} - \frac{{n\rho_{I} \lambda_{g} }}{{\rho_{s} }}} \right)^{L} }}\sqrt {\frac{{4nC_{2} \lambda_{g} }}{{\rho_{s} \lambda_{1} }}} K_{1} \sqrt {\frac{{4nC_{2} \lambda_{g} \lambda_{1} }}{{\rho_{s} }}}$$

(A.9)

Which completes the proof.

$${P}_{2}={\text{Pr}}\left(\frac{{\left(1-\xi \right)P}_{s}{\alpha }_{1}{\left|{g}_{n}\right|}^{2}}{{\left(1-\xi \right)P}_{s}{\alpha }_{2}{\left|{g}_{n}\right|}^{2}+\sum_{i=1}^{L}{P}_{i}{\left|{g}_{i}\right|}^{2}+{N}_{0}}<{\in }_{1},\frac{{\left(1-\xi \right)P}_{s}{\alpha }_{2}{\left|{g}_{n}\right|}^{2}}{\sum_{i=1}^{L}{P}_{i}{\left|{g}_{i}\right|}^{2}+{N}_{0}}<{\in }_{2}\right)+{\text{Pr}}(\frac{{\left(1-\xi \right)P}_{s}{\alpha }_{1}{\left|{g}_{n}\right|}^{2}}{{\left(1-\xi \right)P}_{s}{\alpha }_{2}{\left|{g}_{n}\right|}^{2}+\sum_{i=1}^{L}{P}_{i}{\left|{g}_{i}\right|}^{2}+{N}_{0}}>{\in }_{1},\frac{{\left(1-\xi \right)P}_{s}{\alpha }_{2}{\left|{g}_{n}\right|}^{2}}{\sum_{i=1}^{L}{P}_{i}{\left|{g}_{i}\right|}^{2}+{N}_{0}}>{\in }_{2},\frac{{\alpha }_{1}{P}_{r}^{n}{\left|{h}_{n2}\right|}^{2}}{{\alpha }_{2}{P}_{r}^{n}{\left|{h}_{n2}\right|}^{2}+{N}_{0}}\le {\in }_{1}, \frac{{\alpha }_{1}{P}_{r}^{n}{\left|{h}_{n2}\right|}^{2}}{{N}_{0}}<{\in }_{2})$$

Appendix B

Let,

$$\begin{gathered} {\text{P}}_{2} = P_{2}^{1} + P_{2}^{2} \hfill \\ P_{2}^{1} = \Pr \left( {X \le + \frac{{C_{3} }}{{\rho_{s} }}(CX_{I} + 1} \right) \hfill \\ \end{gathered}$$

(B.1)

where $X = \left| {g_{n} } \right|^{2} ,X_{2} = \left| {h_{n2} } \right|^{2} ,C_{3} = \left( {1 - \xi } \right)\rho_{I} and\, X_{I} = \mathop \sum \limits_{i = 1}^{L} \left| {g_{i} } \right|^{2}.$

$${\text{P}}_{2}^{1} = \mathop \smallint \limits_{0}^{\infty } F_{X} (C_{3} \left( {CX_{i} + 1 } \right)) f_{{X_{I} }} \left( x \right) dx$$

(B.2)

$$P_{2}^{1} = \frac{{\lambda_{I}^{L} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \smallint \limits_{0}^{\infty } \left( {1 - e^{{ - \frac{{\lambda_{g} C_{3} }}{{\rho_{s} }}\left( {Cx + 1} \right)}} } \right)^{M} x^{L - 1} e^{{ - \lambda_{I} x}} dx$$

(B.3)

$$P_{2}^{1} = 1 - \frac{{\lambda_{I}^{L} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} \mathop \smallint \limits_{0}^{\infty } x^{L - 1} e^{{ - n\frac{{\lambda_{g} C_{3} }}{{\rho_{s} }}\left( {Cx + 1} \right) - \lambda_{I} x}} dx$$

(B.4)

$$P_{2}^{1} = 1 - \frac{{\lambda_{I}^{L} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} e^{{ - \frac{{n\lambda_{g} C_{3} }}{{\rho_{s} }}}} \mathop \smallint \limits_{0}^{\infty } x^{L - 1} e^{{x\left( { - \frac{{n\lambda_{g} CC_{3} }}{{\rho_{s} }} - \lambda_{I} } \right)}} dx$$

(B.5)

$$P_{2}^{1} = 1 - \frac{{\lambda_{I}^{L} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} e_{1}^{{ - \frac{{n\lambda_{g} C_{3} }}{{\rho_{s} }}}} \mathop \smallint \limits_{0}^{\infty } x^{L - 1} e^{{ - x\left( {\frac{{n\lambda_{g} CC_{3} }}{{P_{s} }} + \lambda_{I } } \right)}} dx$$

(B.6)

Following $\mathop \smallint \limits_{0}^{\infty } x^{v - 1} e^{ - \mu x} dx = \frac{1}{{\mu^{v} }}\Gamma \left( v \right)$

$$P_{2}^{1} = 1 - \lambda_{I}^{L} \mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\frac{1}{{\left( {\frac{{n\lambda_{g} CC_{3} }}{{\rho_{s} }} + \lambda_{I} } \right)^{L} }}\left( { - 1} \right)^{n + 1} e_{1}^{{ - \frac{{n\lambda_{g} C_{3} }}{{\rho_{s} }}}}$$

(B.7)

$$P_{2}^{2} = \Pr \left( {\frac{{C_{5} }}{{\rho_{S} }} \left( {CX_{I} + 1} \right) < X < \frac{1}{{\rho_{S} }}\left( {\frac{{C_{4} }}{{X_{2} }} - \rho_{I} X_{I} } \right) } \right),$$

(B.8)

$$P_{2}^{2} = \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } \left( {F_{X} \left( {\frac{1}{{\rho_{S} }}\left( {\frac{{C_{4} }}{{X_{2} }} - \rho_{I} X_{I} } \right)} \right) - F_{X} \left( {\frac{{C_{5} }}{{\rho_{S} }} \left( {CX_{I} + 1} \right)} \right)} \right) f_{{X_{i} ,X_{2} }} \left( {x,y} \right) dxdy$$

(B.9)

Let $P_{2}^{2} = Q_{1} - Q_{2}$

$$Q_{1} = \frac{{\lambda_{I}^{L} \lambda_{2} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } \left( {1 - e^{{ - \frac{{\lambda_{g} }}{{\rho_{s} }}\left( {\frac{{C_{4} }}{x} - \rho_{I} y} \right)}} } \right)^{M} e^{{ - \lambda_{2} x}} y^{L - 1} e^{{ - \lambda_{I} y}} dxdy$$

(B.10)

$$= 1 - \frac{{\lambda_{I}^{L} \lambda_{2} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } e^{{ - \frac{{n\lambda_{g} }}{{\rho_{s} }}\left( {\frac{{C_{4} }}{x} - \rho_{I} y} \right)}} e^{{ - \lambda_{2} x}} y^{L - 1} e^{{ - \lambda_{I} y}} dxdy$$

(B.11)

$$= 1 - \frac{{\lambda_{I}^{L} \lambda_{2} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } e_{1}^{{ - \frac{{n\lambda_{g} C_{4} }}{{\rho_{s} x}} - \lambda_{2} x}} y^{L - 1} e^{{ - y\left( {\lambda_{I} - \frac{{n\lambda_{g} \rho_{I} }}{{\rho_{s} }}} \right)}} dxdy$$

(B.12)

$\mathop \smallint \limits_{0}^{\infty } e^{{ - \frac{\beta }{4x} - \lambda x}} = \sqrt {\beta /\lambda } K_{1} \sqrt {\beta \lambda }$ is used to solve above equation further,

$$= 1 - \frac{{\lambda_{I}^{L} \lambda_{2} }}{{{\Gamma }\left( {\text{L}} \right)}}\mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} \sqrt {\frac{{4nC_{4} \lambda_{g} }}{{\rho_{s} \lambda_{2} }}} K_{1} \sqrt {\frac{{4nC_{4} \lambda_{g} \lambda_{2} }}{{\rho_{s} }}} \mathop \smallint \limits_{0}^{\infty } y^{L - 1} e^{{ - y\left( {\lambda_{I} - \frac{{n\lambda_{g} \rho_{I} }}{{\rho_{s} }}} \right)}} dy$$

(B.13)

From (3.381.4) of (Gradshteyn & Ryzhik, 2014), $\mathop \smallint \limits_{0}^{\infty } x^{v - 1} e^{ - \mu x} dx = \frac{1}{{\mu^{v} }}\Gamma \left( v \right)$

$$Q_{1} = 1 - \lambda_{I}^{L} \lambda_{2} \mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {\lambda_{I} - \frac{{n\lambda_{g} \rho_{I} }}{{\rho_{s} }}} \right)^{L} }}\sqrt {\frac{{4nC_{4} \lambda_{g} }}{{\rho_{s} \lambda_{2} }}} K_{1} \sqrt {\frac{{4nC_{4} \lambda_{g} \lambda_{2} }}{{\rho_{s} }}}$$

(B.14)

Following same steps as to evaluate $P_{2}^{1}$ we can also solve

$$Q_{2} = 1 - \lambda_{I}^{L} \mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\frac{{\left( { - 1} \right)^{n + 1} }}{{\left( {\lambda_{I} + \frac{{n\lambda_{g} CC_{5} }}{{\rho_{s} }}} \right)^{L} }}e_{1}^{{ - \frac{{n\lambda_{g} CC_{5} }}{{\rho_{s} }}}}$$

(B.15)

Putting $Q_{1 }$ and $Q_{2}$ to find $P_{2}^{2} ,$ thus it completes the solution.

$$P_{2}^{2} = \lambda_{I}^{L} \mathop \sum \limits_{n = 1}^{M} \left( {\begin{array}{*{20}c} M \\ n \\ \end{array} } \right)\left( { - 1} \right)^{n + 1} \left( {\frac{1}{{\left( {\lambda_{I} - \frac{{n\lambda_{g} \rho_{I} }}{{\rho_{s} }}} \right)^{L} }}\sqrt {\frac{{4nC_{4} \lambda_{g} }}{{\rho_{s} \lambda_{2} }}} K_{1} \sqrt {\frac{{4nC_{4} \lambda_{g} \lambda_{2} }}{{\rho_{s} }}} - \frac{\Gamma \left( L \right)}{{\left( {nC_{1} + \lambda } \right)^{L} }}e_{1}^{{ - nC_{1} N_{0} }} } \right).$$

(B.16)