Skip to main content

Advertisement

Springer Nature Link
Log in

Doa estimation algorithm based on UV decomposition matrix completion

  • Original Paper
  • Published:
Wireless Networks Aims and scope Submit manuscript

Abstract

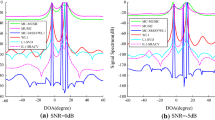
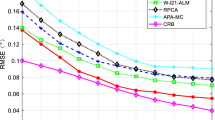
In the imperfect communication environment, the array received signal may have missing data, which could suffer from the direction-of-arrival (DOA) estimation performance deterioration. To this end, the matrix completion method is usually used for recovering the missing data of received signal to improve the DOA estimation accuracy. In this paper, a matrix completion DOA estimation algorithm is proposed based on UV decomposition. Firstly, the array received signal recovery problem is transformed into a matrix completion problem. On this basis, the UV decomposition of the signal is introduced into the matrix completion model, which avoids the singular value decomposition of kernel norm optimization and reduces the computational complexity. In addition, a residual regular term is utilized in the proposed algorithm to reduce the data deviation caused by matrix decomposition. Then, the received signal of the array to be recovered is solved by the alternating direction multiplier method (ADMM) algorithm. Finally, the multiple signal classification (MUSIC) algorithm is used to estimate the DOA of recovered array signal. Simulation results indicate that the proposed algorithm can better recover data to perform DOA estimation with the low computational complexity, and is superior to existing DOA estimation algorithms based on matrix completion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Shi, J., Hu, G., Zhang, X., & Sun, F. (2019). Sparsity-based doa estimation of coherent and uncorrelated targets with flexible mimo radar. IEEE Transactions on Vehicular Technology, 68(6), 5835–5848.

    Article  MATH  Google Scholar 

  2. Wan, L., Liu, K., Liang, Y.-C., & Zhu, T. (2021). Doa and polarization estimation for non-circular signals in 3-d millimeter wave polarized massive mimo systems. IEEE Transactions on Wireless Communications, 20(5), 3152–3167.

    Article  MATH  Google Scholar 

  3. Schmidt, R. (1986). Multiple emitter location and signal parameter estimation. IEEE Transactions on Antennas and Propagation, 34(3), 276–280.

    Article  MathSciNet  MATH  Google Scholar 

  4. Roy, R., & Kailath, T. (1989). Esprit-estimation of signal parameters via rotational invariance techniques. IEEE Transactions on acoustics, speech, and signal processing, 37(7), 984–995.

    Article  MATH  Google Scholar 

  5. Bresler, Y. (1988). Maximum likelihood estimation of a linearly structured covariance with application to antenna array processing. In: Fourth Annual ASSP Workshop on Spectrum Estimation and Modeling, pp. 172–175. IEEE

  6. Ge, C., He, L., Zhou, M.-J., Lin, X.-P., & Zhang, X.-F. (2018). Two-dimensional doa estimation with partial damaged sensors in rectangular array based on tensor reconstruction. In: 2018 4th Annual International Conference on Network and Information Systems for Computers (ICNISC), pp. 299–306. IEEE

  7. Setayesh, A., Yazdian, E., & Malek-Mohammadi, M. (2019). Direction of arrival estimation with missing data via matrix completion. Signal, Image and Video Processing, 13(7), 1451–1459.

    Article  MATH  Google Scholar 

  8. Mohajer, A., Sorouri, F., Mirzaei, A., Ziaeddini, A., Rad, K. J., & Bavaghar, M. (2022). Energy-aware hierarchical resource management and backhaul traffic optimization in heterogeneous cellular networks. IEEE Systems Journal, 16(4), 5188–5199.

    Article  Google Scholar 

  9. Dong, S., Zhan, J., Hu, W., Mohajer, A., Bavaghar, M., & Mirzaei, A. (2023). Energy-efficient hierarchical resource allocation in uplink-downlink decoupled noma hetnets. IEEE Transactions on Network and Service Management

  10. Mohajer, A., Daliri, M. S., Mirzaei, A., Ziaeddini, A., Nabipour, M., & Bavaghar, M. (2022). Heterogeneous computational resource allocation for noma: Toward green mobile edge-computing systems. IEEE Transactions on Services Computing, 16(2), 1225–1238.

    Article  Google Scholar 

  11. Cai, J.-F., Candès, E. J., & Shen, Z. (2010). A singular value thresholding algorithm for matrix completion. SIAM Journal on optimization, 20(4), 1956–1982.

    Article  MathSciNet  MATH  Google Scholar 

  12. Lin, Z., Ganesh, A., Wright, J., Wu, L., Chen, M., & Ma, Y. (2009). Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix. Coordinated Science Laboratory Report no. UILU-ENG-09-2214, DC-246

  13. Chen, Y., Xu, Y., & Li, R. (2016). An alm matrix completion algorithm for recovering weather monitoring data. In: 2016 IEEE Symposium on Computers and Communication (ISCC), pp. 988–995. IEEE

  14. Wang, X., Zhu, Y., Huang, M., Wang, J., Wan, L., & Bi, G. (2019). Unitary matrix completion-based doa estimation of noncircular signals in nonuniform noise. IEEE Access, 7, 73719–73728.

    Article  MATH  Google Scholar 

  15. Fei, Y., Cao, H., Wu, Y., Chen, X., & Chen, L. (2021). Doa estimation in non-uniform noise using matrix completion via alternating projection. IEEE Open Journal of Antennas and Propagation, 2, 281–285.

    Article  MATH  Google Scholar 

  16. Jalal, B., Elnahas, O., & Quan, Z. (2022). Efficient doa estimation under partially impaired antenna array elements. IEEE Transactions on Vehicular Technology, 71(7), 7991–7996.

    Article  MATH  Google Scholar 

  17. Chen, J., Gao, W., & Wei, K. (2021). Exact matrix completion based on low rank hankel structure in the fourier domain. Applied and Computational Harmonic Analysis, 55, 149–184.

    Article  MathSciNet  MATH  Google Scholar 

  18. Mazumder, R., Hastie, T., & Tibshirani, R. (2010). Spectral regularization algorithms for learning large incomplete matrices. The Journal of Machine Learning Research, 11, 2287–2322.

    MathSciNet  MATH  Google Scholar 

  19. Bokaei, M., Razavikia, S., Amini, A., & Rini, S. (2022). Single-snapshot doa estimation via weighted hankel-structured matrix completion. In: 2022 30th European Signal Processing Conference (EUSIPCO), pp. 1756–1760. IEEE

  20. Jiang, G., Mao, X.-P., & Liu, Y.-T. (2020). Underdetermined doa estimation via covariance matrix completion for nested sparse circular array in nonuniform noise. IEEE Signal Processing Letters, 27, 1824–1828.

    Article  MATH  Google Scholar 

  21. Zhao, J., Liang, Y., Yi, S., Shen, Q., & Cao, X. (2023). Improving generalization of double low-rank representation using schatten-p norm. Pattern Recognition, 138, 109352.

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 61971117) the Natural Science Foundation of Hebei Province (Grant No. F2024501005) and the \(\mathrm {S \& T }\) Program of Hebei (No. 22377717D).

Author information

Authors and Affiliations

  1. Laboratory of Cognitive Radio and Big Spectrum Data Processing, Hebei Key Laboratory of Marine Perception Network and Data Processsing, Northeastern University at Qinhuangdao, Qinhuangdao, 066004, China

    Fulai Liu & Ruiyan Du

  2. School of Computer Science and Engineering, Northeastern University, Shenyang, 110819, China

    Guangyu Meng, Bo Zhang, Aiyi Zhang & Xinyue Lou

Authors
  1. Fulai Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guangyu Meng
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Bo Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Aiyi Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Xinyue Lou
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Ruiyan Du
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Fulai Liu or Guangyu Meng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, F., Meng, G., Zhang, B. et al. Doa estimation algorithm based on UV decomposition matrix completion. Wireless Netw 31, 2317–2326 (2025). https://doi.org/10.1007/s11276-024-03883-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11276-024-03883-2

Keywords