Performance Analysis of Incremental Amplify-and-Forward Relaying Protocols with Nth Best Partial Relay Selection Under Interference Constraint

Abstract

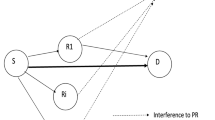
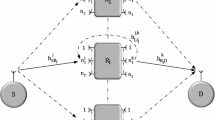
In this paper, we investigate two incremental amplify-and-forward relaying protocols in cognitive underlay networks. In the proposed protocols, whenever the secondary destination cannot receive the secondary source’s signal successfully, it requests a retransmission from one of M secondary relays. In the first protocol, we assume that a secondary relay with the Nth best channel gain to the secondary source is used to forward the received signal to the secondary destination. In the second protocol, relying on the quality of channels between the secondary relay and secondary destination and between the secondary relay and primary user, the Nth best relay is chosen for the retransmission. We derive exact closed-form expressions of the outage probability and average number of time slots for both protocols over Rayleigh fading channel. Finally, these mathematical expressions are then verified by Monte Carlo simulations.

Appendices

Appendix A: Derivation of (8)

Relying on [16], the CDF and PDF, respectively, of the RVs $\psi _2$ are given as

$$\begin{aligned} F_{\psi _2} \left(x\right)&= \frac{\lambda _2 x}{\lambda _2 x+\lambda _4 Q},\end{aligned}$$

(25)

$$\begin{aligned} f_{\psi _2} \left(x\right)&= \frac{\lambda _2 \lambda _4 Q}{\left({\lambda _2 x+\lambda _4 Q}\right)^{2}} \end{aligned}$$

(26)

Setting $w = \gamma _3$; the outage probability $\text{ P}_{\mathrm{IAF1}}^{\mathrm{out}}$ conditioned on $\gamma _3$ is calculated as

$$\begin{aligned} \text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)&= \Pr \left[{\psi _0 <\gamma _{th}, \gamma _1^{AF} < \gamma _{th} |\gamma _3} \right] \nonumber \\&= \Pr \left[{Q\frac{\gamma _0}{w}<\gamma _{th}}\right]\Pr \left[{\frac{\psi _1 \psi _2}{\psi _1 + \psi _2 +1}<\gamma _{th} |\gamma _3}\right] \nonumber \\&= \Pr \left[{\gamma _0 <\rho w}\right] \left[{F_{\psi _2} \left({\gamma _{th}}\right)+\int \limits _{\gamma _{th}}^{+\infty } {F_{\psi _1 |\gamma _3} \left({\frac{\gamma _{th} x+\gamma _{th}}{x-\gamma _{th}}} \right)f_{\psi _2} \left(x\right)dx}}\right]\nonumber \\ \end{aligned}$$

(27)

where $\rho = \gamma _{th} /Q$ and $F_{\psi _1 | \gamma _3} \left(.\right)$ is the CDF of $\psi _1$ conditioned on $\gamma _3$, which can be given by using (5) as

$$\begin{aligned} F_{\psi _1|\gamma _3} \left(x\right)&= \Pr \left[{Q\frac{\gamma _{1b}}{w}<x}\right]=F_{\gamma _{1b}} \left({\frac{wx}{Q}}\right) \nonumber \\&= 1+\sum _{n=1}^N {\sum _{m=0, n+m > 1}^{M-n+1} {\left({-1}\right)^{m}} C_M^{n-1} C_{M-n+1}^m \exp \left({-\frac{\left({n+m-1}\right)\lambda _1 w}{Q}x}\right)}\nonumber \\ \end{aligned}$$

(28)

Substituting (25), (26) and (28) into (27), we obtain (29) as

$$\begin{aligned} \text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)&= \left({1-\exp \left({-\lambda _0 \rho w}\right)}\right) \nonumber \\&\times \left[{1+\sum _{n=1}^N {\sum _{m=0, n+m > 1}^{M-n+1} {\left({-1}\right)^{m}} C_M^{n-1} C_{M-n+1}^m \lambda _2 \lambda _4 Q\underbrace{\int \limits _{\gamma _{th}}^{+\infty } {\dfrac{\exp \left({-\left({n+m-1}\right)\lambda _1 \rho w\dfrac{x+1}{x-\gamma _{th}}} \right)}{\left({\lambda _2 x+\lambda _4 Q} \right)^{2}}dx}}_{I_1}}} \right]\nonumber \\ \end{aligned}$$

(29)

Now, we consider the integral $I_1$ in (29). First, by setting $y=1+\frac{\lambda _2 \gamma _{th} +\lambda _4 Q}{\lambda _2 \left({x-\gamma _{th}} \right)}$, we can respectively get

$$\begin{aligned} \lambda _2 x + \lambda _4 Q&= \frac{\left({\lambda _2 \gamma _{th} +\lambda _4 Q}\right)y}{y-1},\end{aligned}$$

(30)

$$\begin{aligned} \frac{x+1}{x-\gamma _{th}}&= \frac{\lambda _2 \left({1+\gamma _{th}} \right)y+\lambda _4 Q-\lambda _2}{\lambda _4 Q+\lambda _2 \gamma _{th}},\end{aligned}$$

(31)

$$\begin{aligned} dy&= -\frac{\lambda _2 \gamma _{th} + \lambda _4 Q}{\lambda _2 \left({x-\gamma _{th}}\right)^{2}}dx = -\frac{\lambda _2 \left({y-1}\right)^{2}}{\lambda _2 \gamma _{th} + \lambda _4 Q}dx \end{aligned}$$

(32)

Therefore, by using the change of variable $y=1+\frac{\lambda _2 \gamma _{th} + \lambda _4 Q}{\lambda _2 \left({x-\gamma _{th}}\right)}$ and results given in (30–32), we can express the integral $I_1$ under the following form:

$$\begin{aligned} I_1&= \int \limits _{+\infty }^0 {\frac{\left({y-1}\right)^{2}}{\left({\lambda _2 \gamma _{th} +\lambda _4 Q} \right)^{2}y^{2}}\exp \left({-\left({n+m-1}\right)\lambda _1 \rho w\frac{\lambda _2 \left({1+\gamma _{th}} \right)y+\lambda _4 Q-\lambda _2}{\lambda _4 Q+\lambda _2 \gamma _{th}}}\right)\left({-\frac{\lambda _2 \gamma _{th} +\lambda _4 Q}{\lambda _2 \left({y-1}\right)^{2}}dy}\right)} \nonumber \\&= \frac{1}{\lambda _2 \left({\lambda _2 \gamma _{th} +\lambda _4 Q} \right)}\exp \left({-\left({n+m-1} \right)\lambda _1 \rho w\frac{\lambda _4 Q-\lambda _2}{\lambda _4 Q+\lambda _2 \gamma _{th}}} \right) \nonumber \\&\times \int \limits _0^{+\infty } {\frac{1}{y^{2}}\exp \left({-\left({n+m-1} \right)\lambda _1 \rho w\frac{\lambda _2 \left({1+\gamma _{th}} \right)y}{\lambda _4 Q+\lambda _2 \gamma _{th}}} \right)dy} \end{aligned}$$

(33)

Substituting (33) into (29), we can rewrite $\text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)$ as follows:

$$\begin{aligned}&\text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)= \left({1-\exp \left({-\lambda _0 \rho w}\right)}\right)\nonumber \\&\quad \left[{\begin{array}{l} 1+\sum _{n=1}^N {\sum _{m=0, n+m > 1}^{M-n+1} {\left({-1} \right)^{m}} C_M^{n-1} C_{M-n+1}^m \dfrac{\lambda _4 Q\exp \left({-\Omega \left({\lambda _4 Q-\lambda _2} \right)w} \right)}{\lambda _2 \gamma _{th} +\lambda _4 Q}} \\ \times \int _1^{+\infty } {\dfrac{\exp \left({-\Omega \lambda _2 \left({1+\gamma _{th}} \right)wy} \right)}{y^{2}}} dy \\ \end{array}} \right],\qquad \quad \end{aligned}$$

(34)

where $\Omega = \frac{\left({n+m-1}\right) \lambda _1 \rho }{\lambda _2 \gamma _{th} + \lambda _4 Q}$.

Because

$\int \limits _1^{+\infty } {\frac{\exp \left({-\Omega \lambda _2 \left({1+\gamma _{th}}\right)wy}\right)}{y^{2}}} dy\!=\!\exp \left({\!-\!\Omega \lambda _2 \left({1\!+\!\gamma _{th}}\right)w} \right)\!-\!\Omega \lambda _2 \left({1\!+\!\gamma _{th}}\right)wE_1 \left({\Omega \lambda _2 \left({1\!+\!\gamma _{th}}\right)w} \right)$, where $E_1 \left(.\right)$ is exponential integral, we obtain (35) from (34) as follows:

$$\begin{aligned} \text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)&= 1-\exp \left({-\lambda _0 \rho w}\right)+\sum _{n=1}^N {\sum _{m=0, n+m > 1}^{M-n+1} {\left({-1}\right)^{m}} C_M^{n-1} C_{M-n+1}^m \frac{\lambda _4 Q}{\lambda _2 \gamma _{th} +\lambda _4 Q}} \nonumber \\&\times \left[{\begin{array}{l} \exp \left({-\Omega \left({\lambda _2 \gamma _{th} +\lambda _4 Q} \right)w} \right)-\exp \left({-\left({\Omega \left({\lambda _2\gamma _{th} +\lambda _4 Q}\right)+\lambda _0 \rho }\right)w}\right)\\ \,-\,\Omega \lambda _2 \left({1+\gamma _{th}}\right)w\exp \left({-\Omega \left({\lambda _4 Q-\lambda _2}\right)w}\right)E_1 \left({\Omega \lambda _2 \left({1+\gamma _{th}}\right)w} \right)\\ \,+\,\Omega \lambda _2 \left({1+\gamma _{th}} \right)w\exp \left({-\left({\Omega \left({\lambda _4 Q-\lambda _2} \right)+\lambda _0 \rho } \right)w} \right)E_1 \left({\Omega \lambda _2 \left({1+\gamma _{th}} \right)w} \right) \\ \end{array}}\right]\nonumber \\ \end{aligned}$$

(35)

Similar to [14], the probability $\text{ P}_{\mathrm{IAF1}}^{\mathrm{out}}$ can be formulated as

$$\begin{aligned} \text{ P}_{\mathrm{IAF1}}^{\mathrm{out}} =\int \limits _0^{+\infty } {\text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)f_{\gamma _3} \left(w\right)dw} = \int \limits _0^{+\infty } {\text{ P}_{\mathrm{IAF1|}\gamma _3}^{\mathrm{out}} \left(w\right)\lambda _3 \exp \left({-\lambda _3 w}\right)dw} \end{aligned}$$

(36)

In addition, with a, b and c as positive constants, we have (33) as

$$\begin{aligned} \int \limits _0^{+\infty } {\left({ax}\right)b\exp \left({-cx}\right)E_1 \left({ax}\right)dx} = \frac{ab}{c^{2}}\left[{\ln \left({\frac{a+c}{a}}\right)-\frac{c}{a+c}}\right] \end{aligned}$$

(37)

Now, we substitute (35) into (36), then we use (37) to calculate the corresponding integral. After some careful manipulation, we obtain (8).

Appendix B: Derivation of (12)

Similar to (27), by setting $w=\gamma _3$, the outage probability $\text{ P}_{\mathrm{IAF2}}^{\mathrm{out}}$ conditioned on $\gamma _3$ is calculated as

$$\begin{aligned} \text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)=\Pr \left[{\gamma _0 <w\rho }\right] \left[{F_{\psi _3}\left({\gamma _{th}} \right)+\int \limits _{\gamma _{th}}^{+\infty } {F_{\psi _3 |\gamma _3} \left({\frac{\gamma _{th} x+\gamma _{th}}{x-\gamma _{th}}} \right)f_{\psi _4}\left(x\right)dx}}\right].\nonumber \\ \end{aligned}$$

(38)

By using $F_{\psi _3 |\gamma _3} \left(x\right)=1-\exp \left({-\frac{\lambda _3 wx}{Q}}\right)$ and (10) for (38), we obtain

$$\begin{aligned} \text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)&= \left({1-\exp \left({-\lambda _0 \rho w}\right)} \right) \nonumber \\&\times \left[{1\!-\!\frac{M!}{\left({N-1}\right)!\left({M-N} \right)!}\left({\kappa Q}\right)^{N}\int \limits _{\gamma _{th}}^{+\infty } {\frac{x^{M-N}}{\left({x+\kappa Q}\right)^{M+1}}\exp \left({-\lambda _3 \rho w\frac{x+1}{x-\gamma _{th}}}\right)dx}} \right]\!.\nonumber \\ \end{aligned}$$

(39)

Now, by applying the change of variable $y=\frac{x+\kappa Q}{x-\gamma _{th}}$, we rewrite (39) as

$$\begin{aligned} \text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)&\!=\!&\left({1-\exp \left({-\lambda _0 \rho w}\right)}\right) \left[{\begin{array}{l} 1-\frac{M!}{\left({N-1}\right)!\left({M-N}\right)!} \frac{\gamma _{th}^{M-N}\left({\kappa Q}\right)^{N}}{\left({\gamma _{th} + \kappa Q}\right)^{M}}\exp \left({-\Delta \left({\kappa Q-1}\right)w}\right) \\ \times \int \limits _1^{+\infty } {\frac{\left({y+\frac{\kappa }{\rho }} \right)^{M-N}\left({y-1}\right)^{N-1}}{y^{M+1}}\exp \left({-\Delta \left({1+\gamma _{th}}\right)wy}\right)dy} \end{array}} \right]\nonumber \\ \end{aligned}$$

(40)

where $\Delta = \frac{\lambda _3 \rho }{\gamma _{th} + \kappa Q}$.

Using binomial expansion for $\left({y+\frac{\kappa }{\rho }}\right)^{M-N}$ and $\left({y-1}\right)^{N-1}$ in (40), we have

$$\begin{aligned} \text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)&= \left({1-\exp \left({-\lambda _0 \rho w}\right)}\right) \nonumber \\&\times \left[{\begin{array}{l} 1-\dfrac{M!}{\left({N-1} \right)!\left({M-N} \right)!}\dfrac{\gamma _{th}^{M-N} \left({\kappa Q} \right)^{N}}{\left({\gamma _{th} +\kappa Q} \right)^{M}}\exp \left({-\Delta \left({\kappa Q-1}\right)w} \right) \\ \times \sum \limits _{i=0}^{M-N} {\sum \limits _{j=0}^{N-1} {\left({-1} \right)^{N-1-j}C_{M-N}^i C_{N-1-j}^j \left({\dfrac{\kappa }{\rho }} \right)}}^{M-N-i}\underbrace{\int \limits _1^{+\infty } {\dfrac{\exp \left({-\Delta \left({1+\gamma _{th}} \right)wy} \right)}{y^{M-i-j+1}}dy}}_{J_1} \\ \end{array}}\right].\nonumber \\ \end{aligned}$$

(41)

Applying [17, 3.351.4], for the integral $J_1$ in (42) and $E_1\left(x\right) = -E_i \left({-x}\right)$, we can obtain (42) as

$$\begin{aligned} \text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)&= 1-\exp \left({-\lambda _0 \rho w}\right)\nonumber \\&-\dfrac{M!}{\left({N-1} \right)!\left({M-N} \right)!}\frac{\gamma _{th}^{M-N} \left({\kappa Q} \right)^{N}}{\left({\gamma _{th} +\kappa Q} \right)^{M}}\sum _{i=0}^{M-N} {\sum _{j=0}^{N-1} {\left({-1} \right)^{N-1-j}C_{M-N}^i C_{N-1-j}^j \left({\frac{\kappa }{\rho }} \right)}}^{M-N-i} \nonumber \\&\!\times \! \left\{ {\begin{array}{l} \left({-1} \right)^{M-i-j}\frac{\left({\Delta \left({1+\gamma _{th}} \right)} \right)^{M-i-j}}{\left({M-i-j} \right)!} \left[{\begin{array}{l} w^{M-i-j}\exp \left({-\Delta \left({\kappa Q-1}\right)w} \right)E_1 \left({\Delta \left({1+\gamma _{th}}\right)w}\right)\\ -w^{M-i-j}\exp \left({-\left({\Delta \left({\kappa Q-1} \right)+\lambda _0 \rho } \right)w} \right)E_1 \left({\Delta \left({1+\gamma _{th}} \right)w} \right) \\ \end{array}} \right] \\ +\sum \limits _{u=0}^{M-i-j-1} {\frac{\left({-1}\right)^{u}\left({\Delta \left({1+\gamma _{th}}\right)}\right)^{u}}{\prod _{z=0}^u {\left({M-i-j-z}\right)}} \left[{\begin{array}{l} w^{u}\exp \left({-\Delta \left({\gamma _{th} +\kappa Q} \right)w} \right) \\ -w^{u}\exp \left({-\left({\Delta \left({\gamma _{th} +\kappa Q} \right)+\lambda _0 \rho } \right)w} \right) \\ \end{array}} \right]} \\ \end{array}} \right\} \nonumber \\ \end{aligned}$$

(42)

Also, the probability $\text{ P}_{\mathrm{IAF2}}^{\mathrm{out}}$ can be formulated as

$$\begin{aligned} \text{ P}_{\mathrm{IAF2}}^{\mathrm{out}} = \int \limits _0^{+\infty } {\text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right) f_{\gamma _3} \left(w\right)dw} = \int \limits _0^{+\infty } {\text{ P}_{\mathrm{IAF2|}\gamma _3}^{\mathrm{out}} \left(w\right)\lambda _3 \exp \left({-\lambda _3 w}\right)dw} \end{aligned}$$

(43)

Now, we substitute (42) into (43) and use [17, 6.228.2] with $E_1\left(x\right)=-E_i \left({-x}\right)$ for the corresponding integrals to obtain (12).