Closed-Form Solutions to the Pareto Boundary and Distributed Beamforming Strategy for the Two-User MISO Interference Channel

Abstract

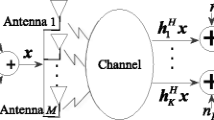
The outer boundary of the achievable rate region for multiple-input single-output (MISO) interference channel (IC) is Pareto boundary, and all points on the Pareto boundary can be obtained by solving weighted sum rate maximization problem. Unfortunately, since the optimization problem is non-convex, it is generally very difficult to obtain the solutions without performing an exhaustive search. In this paper, the achievable rate region of the two-user MISO IC is considered. Firstly, by minimizing the interference power leaked to the other receiver for fixed useful signal power received at the intended receiver, the non-convex optimization problem is converted into a family of convex optimization problems. Secondly, after some conversions, the closed-form solutions to all Pareto optimal points are derived using the Lagrange duality theory, and the only computation involved is to solve a basic quadratic equation. Then, the antenna reduction is performed to further simplify the process of derivation. In order to avoid the exchange of channel state information (CSI) between base stations, a distributed iterative beamforming strategy which can achieve a approximate Pareto optimal outcome with only a few iterations is also proposed. Finally, the results are validated via numerical simulations.

Appendices

Appendix A

1.1 Proof of Proposition 1

Write the direct link channel vector ${\tilde{\mathbf{h}}}_{kk}$ as a scalar multiple of the interference channel vector ${\tilde{\mathbf{h}}}_{k{\overline{k}}}$ plus a vector ${\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot$ which is orthogonal to ${\tilde{\mathbf{h}}}_{k{\overline{k}}}$

$$\begin{aligned} {\tilde{\mathbf{h}}}_{kk} =\omega _k {\tilde{\mathbf{h}}}_{k{\overline{k}}} +{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot . \end{aligned}$$

(17)

Since ${\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot$ is orthogonal to ${\tilde{\mathbf{h}}}_{k{\overline{k}}}$, we can obtain

$$\begin{aligned} \langle {\begin{array}{ll} {{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot ,}&{{\tilde{\mathbf{h}}}_{k{\overline{k}}}} \\ \end{array} }\rangle =\langle {\begin{array}{ll} {{\tilde{\mathbf{h}}}_{kk} -\omega _k {\tilde{\mathbf{h}}}_{k{\overline{k}}},}&{{\tilde{\mathbf{h}}}_{k{\overline{k}}}} \\ \end{array}}\rangle =0. \end{aligned}$$

(18)

Solving the Eq. (18) for $\omega _k$, we can get

$$\begin{aligned} \omega _k =\frac{\langle {\begin{array}{ll} {{\tilde{\mathbf{h}}}_{k{\overline{k}}},}&{{\tilde{\mathbf{h}}}_{kk}} \\ \end{array} }\rangle }{\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}} } \right\Vert^{2}}. \end{aligned}$$

(19)

Then the orthogonal vector ${\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot$ can be expressed as

$$\begin{aligned} {\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot ={\tilde{\mathbf{h}}}_{kk} -\frac{\langle {\begin{array}{ll} {{\tilde{\mathbf{h}}}_{k{\overline{k}}},}&{{\tilde{\mathbf{h}}}_{kk} } \\ \end{array} }\rangle }{\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}} } \right\Vert^{2}}{\tilde{\mathbf{h}}}_{k{\overline{k}}}. \end{aligned}$$

(20)

Now define $\mathbf{U}_k$ as a unitary matrix. Let $\frac{{\tilde{\mathbf{h}}}_{k{\overline{k}}}}{\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}}} \right\Vert}$ be the first column and $\frac{{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot }{\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot } \right\Vert}$ be the second column of the $\mathbf{U}_k$. With the definition of

$$\begin{aligned} {\overline{\mathbf{w}}}{\mathop {=}\limits ^{\Delta }} \mathbf{U}_k^H {\tilde{\mathbf{w}}}_k, \end{aligned}$$

(21)

the received signal at $\text{ MS}_k$ in (1) can be rewritten as (22).

$$\begin{aligned} y_k&= {\tilde{\mathbf{h}}}_{kk}^H \mathbf{U}_k {\overline{\mathbf{w}}}_k s_k +{\tilde{\mathbf{h}}}_{{\overline{k}}k}^H \mathbf{U}_{{\overline{k}}} {\overline{\mathbf{w}}}_{{\overline{k}}} s_{{\overline{k}}} +n_k\nonumber \\&= \left[{{\begin{array}{l} {\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}} }{\left\Vert {\widetilde{\mathbf{h}}_{k{\overline{k}}} } \right\Vert\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert}}\\ {\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}}^\bot }{\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert\left\Vert {\widetilde{\mathbf{h}}_{k{\overline{k}}}^\bot } \right\Vert}}\\ {\mathbf{0}_{\left( {N_t -2} \right)\times 1} } \\ \end{array}}} \right]^{H}\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert{\overline{\mathbf{w}}}_k s_k + \left[ {{\begin{array}{l} {\frac{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}k} } \right\Vert}{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}{\overline{k}}} } \right\Vert}}\\ 0 \\ {\mathbf{0}_{\left( {N_t -2} \right)\times 1} } \\ \end{array}}}\right]^{H}\left\Vert{\widetilde{\mathbf{h}}_{{\overline{k}}{\overline{k}}} } \right\Vert{\overline{\mathbf{w}}}_{{\overline{k}}} s_{{\overline{k}}} +n_k \end{aligned}$$

(22)

From the Eq. (22), we can find that the received signal $y_k$ doesn’t depend on the channel inputs $\bar{{w}}_{k,3} s_k$ to $\bar{{w}}_{k,N_t } s_k$ and $\bar{{w}}_{{\overline{k}},3} s_{{\overline{k}}}$ to $\bar{{w}}_{{\overline{k}},N_t } s_{{\overline{k}}}$ where $\bar{{w}}_{k,i}$ denotes the $i\text{ th}$ entry of beamforming vector ${\overline{\mathbf{w}}}_k$, and hence, they can be dropped. Define

$$\begin{aligned} \mathbf{w}_k {\mathop {=}\limits ^{\Delta }} \left\Vert{{\tilde{\mathbf{h}}}_{kk}} \right\Vert\left[ {{\begin{array}{l} {{\overline{w}}_{k,1} } \\ {{\overline{w}}_{k,2} } \\ \end{array} }} \right], \end{aligned}$$

(23)

and remove the irrelevant dimensions, we can obtain the following standard form of the equivalent channel

$$\begin{aligned} y_k =\left[ {{\begin{array}{l} {\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}} }{\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert\left\Vert {\widetilde{\mathbf{h}}_{k{\overline{k}}} } \right\Vert}} \\ {\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}}^\bot }{\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot } \right\Vert}} \\ \end{array} }} \right]^{H}\mathbf{w}_k s_k +\left[ {{\begin{array}{l} {\frac{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}k} } \right\Vert}{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}{\overline{k}}} } \right\Vert}} \\ 0 \\ \end{array} }} \right]^{H}\mathbf{w}_{{\overline{k}}} s_{{\overline{k}}} +n_k,\quad k=1,2. \end{aligned}$$

(24)

Consequently, the parameters of the equivalent channel can be expressed as the Eqs. (3), (4) and (5) respectively. $\square$

Appendix B

1.1 Proof of Theorem 1

Inspired by [19], we give the following proof. From the definition of the Pareto optimality, we know that every point on the Pareto boundary is uniquely defined when either of the user rate is known. Hence, we can derive the Pareto boundary by solving the optimization problem of maximizing one rate for a given value of the other rate

$$\begin{aligned} \begin{array}{l} \mathop {\text{ maximize}}\limits _{\mathbf{w}_k,\mathbf{w}_{{\overline{k}}} } \quad R_k \left( {\mathbf{w}_k,\mathbf{w}_{{\overline{k}}} } \right) \\ \text{ subject} \text{ to}\quad R_{{\overline{k}}} \left( {\mathbf{w}_{{\overline{k}}},\mathbf{w}_k } \right)=R_{{\overline{k}}}^{*} \quad \quad k=1,2, \\ \end{array} \end{aligned}$$

(25)

From the viewpoint of game theory [21], the minimum $\underline{R}_k$ and maximum $\overline{R} _k$ Pareto optimal rates of $\text{ MS}_k$ can be explicitly written as functions of the selfish (MRT) and altruistic (ZF) transmit strategies with full transmit power used as follows

$$\begin{aligned} \underline{R}_k&= R_k \left( {\sqrt{P_k }\mathbf{w}_k^{\mathrm{ZF}} ,\sqrt{P_{{\overline{k}}} }\mathbf{w}_{{\overline{k}}}^{\mathrm{MRT}} } \right),\end{aligned}$$

(26)

$$\begin{aligned} \overline{R}_k&= R_k \left( {\sqrt{P_k }\mathbf{w}_k^{\mathrm{MRT}} ,\sqrt{P_{{\overline{k}}} }\mathbf{w}_{{\overline{k}}}^{\mathrm{ZF}} } \right). \end{aligned}$$

(27)

As long as $R_k$ is chosen in the range $\left[ {\underline{R}_k ,\overline{R} _k } \right]$, there always exists a feasible solution to optimization problem of (25).

Assume that the Pareto optimal beamforming vector $\mathbf{w}_{{\overline{k}}}^{*}$ known, the problem (25) reduces to

$$\begin{aligned} \begin{array}{l} \mathop {\text{ maximize}}\limits _{\mathbf{w}_k } \quad R_{{\overline{k}}} \left( {\mathbf{w}_{{\overline{k}}}^{*},\mathbf{w}_k } \right) \\ \text{ subject} \text{ to}\quad R_k \left( {\mathbf{w}_k,\mathbf{w}_{{\overline{k}}}^{*} } \right)=R_k^{*},\quad k=1,2, \\ \end{array} \end{aligned}$$

(28)

where the optimization is only with respect to $\mathbf{w}_k$. From the expression of user rate in (7), we can find that $R_{{\overline{k}}}$ is monotonously decreasing with the interference power from $\text{ BS}_k$ and $R_k$ is monotonously increasing with the useful signal power from $\text{ BS}_k$ while useful signal power and interference power from $\text{ BS}_{{\overline{k}}}$ are fixed. Thus, the optimization problem of (28) can be equivalently written as

$$\begin{aligned} \begin{array}{l} \mathop {\text{ minimize}}\limits _{\mathbf{w}_k } \quad \mathbf{w}_k^H \mathbf{h}_{k{\overline{k}}} \mathbf{h}_{k{\overline{k}}}^H \mathbf{w}_k \\ \text{ subject} \text{ to}\quad \mathbf{w}_k^H \mathbf{h}_{kk} \mathbf{h}_{kk}^H \mathbf{w}_k =u_k^{*}, \\ \quad \quad \quad \quad \quad \quad \mathbf{w}_k^H \mathbf{w}_k \le P_k,\quad k=1,2, \\ \end{array} \end{aligned}$$

(29)

where $u_k^{*}$ is the correspondingly useful signal power according to $R_k^{*}$. So, through minimizing the interference power subject to a specific bound $u_k$ defined in (10), we can obtain the Pareto optimal points. $\square$

Appendix C

1.1 Proof of Theorem 2

The problem (9) can be rewritten as

$$\begin{aligned} \begin{array}{l} \mathop {\text{ minimize}}\limits _{\mathbf{w}_k } \quad \mathbf{w}_k^H \mathbf{h}_{k{\overline{k}}} \mathbf{h}_{k{\overline{k}}}^H \mathbf{w}_k \\ \text{ subject} \text{ to}\quad \mathbf{w}_k^H \frac{\mathbf{h}_{kk} }{\sqrt{u_k }}\left( {\frac{\mathbf{h}_{kk} }{\sqrt{u_k }}} \right)^{H}\mathbf{w}_k =1, \\ \quad \quad \quad \quad \quad \quad \mathbf{w}_k^H \mathbf{w}_k \le P_k,\quad k=1,2. \\ \end{array} \end{aligned}$$

(30)

Since single-antenna receivers assumed, the rank of matrix $\frac{\mathbf{h}_{kk} }{\sqrt{u_k }}\left( {\frac{\mathbf{h}_{kk} }{\sqrt{u_k }}} \right)^{H}$ is one. Thus the first constraint can be replaced by the linear constraint $\mathbf{w}_k^H \frac{\mathbf{h}_{kk} }{\sqrt{u_k }}=1$ [22, 23], and the problem (30) reduces to

$$\begin{aligned} \begin{array}{l} \mathop {\text{ minimize}}\limits _{\mathbf{w}_k } \quad \mathbf{w}_k^H \mathbf{h}_{k{\overline{k}}} \mathbf{h}_{k{\overline{k}}}^H \mathbf{w}_k \\ \text{ subject} \text{ to}\quad \mathbf{w}_k^H \frac{\mathbf{h}_{kk} }{\sqrt{u_k }}=1, \\ \quad \quad \quad \quad \quad \quad \mathbf{w}_k^H \mathbf{w}_k \le P_k,\quad k=1,2. \\ \end{array} \end{aligned}$$

(31)

Set

$$\begin{aligned} \mathbf{B}&= \mathbf{h}_{k{\overline{k}}} \mathbf{h}_{k{\overline{k}}}^H = \left[ {{\begin{array}{ll} b&0 \\ 0&0 \\ \end{array} }} \right],\end{aligned}$$

(32)

$$\begin{aligned} \mathbf{a}&= \frac{\mathbf{h}_{kk} }{\sqrt{u_k }}=\frac{1}{\sqrt{u_k }} \left[ {{\begin{array}{l} m \\ n \\ \end{array} }} \right], \end{aligned}$$

(33)

where $b=\frac{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}k} } \right\Vert^{2}}{\left\Vert {\widetilde{\mathbf{h}}_{{\overline{k}}{\overline{k}}} } \right\Vert^{2}},\,m=\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}} }{\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert\left\Vert {\widetilde{\mathbf{h}}_{k{\overline{k}}} } \right\Vert}$ and $n=\frac{\widetilde{\mathbf{h}}_{kk}^H \widetilde{\mathbf{h}}_{k{\overline{k}}}^\bot }{\left\Vert {\widetilde{\mathbf{h}}_{kk} } \right\Vert\left\Vert {{\tilde{\mathbf{h}}}_{k{\overline{k}}}^\bot } \right\Vert}$. The Lagrangian of (31) is

$$\begin{aligned} \mathcal{L }\left( {\mathbf{w}_k,\lambda ,\mu } \right)=\mathbf{w}_k^H \mathbf{Bw}_k +\lambda \left( {\mathbf{w}_k^H \mathbf{a}-1} \right)+\mu \left( {\mathbf{w}_k^H \mathbf{w}_k -P_k } \right), \end{aligned}$$

(34)

where $\lambda$ and $\mu$ are the Lagrange multipliers associated with the problem (31).

From the Karush-Kuhn-Tucker (KKT) conditions [24–26], we can obtain

$$\begin{aligned} \frac{\partial \mathcal{L }\left( {\mathbf{w}_k,\lambda ,\mu } \right)}{\partial \mathbf{w}_k }&= 2\mathbf{Bw}_k +\lambda \mathbf{a}+2\mu \mathbf{w}_k =0,\end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial \mathcal{L }\left( {\mathbf{w}_k,\lambda ,\mu } \right)}{\partial \lambda }&= \mathbf{w}_k^H \mathbf{a}-1=0,\end{aligned}$$

(36)

$$\begin{aligned} \frac{\partial \mathcal{L }\left( {\mathbf{w}_k,\lambda ,\mu } \right)}{\partial \mu }&= \mathbf{w}_k^H \mathbf{w}_k -P_k =0. \end{aligned}$$

(37)

Since the primal problem (9) is convex, all solutions to the KKT conditions will yield Pareto optimal points [25]. From Eq. (35), we get

$$\begin{aligned} \mathbf{w}_k^{*} =-\frac{1}{2}\lambda \left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-1}\mathbf{a}, \end{aligned}$$

(38)

where $\mathbf{I}$ denotes the identity matrix of size $N_t \times N_t$. Submit (38) into (36) and (37), we get

$$\begin{aligned}&\lambda \mathbf{a}^{H}\left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-1}\mathbf{a}+2=0,\end{aligned}$$

(39)

$$\begin{aligned}&\lambda ^{2}\mathbf{a}^{H}\left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-2}\mathbf{a}-4P_k =0. \end{aligned}$$

(40)

From the expression of $\mathbf{B}$ defined in (32), we can get the expression of $\left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-1}$ and $\left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-2}$ as

$$\begin{aligned} \left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-1}&= \left[ {{\begin{array}{ll} {\frac{1}{b+\mu }}&\\&{\frac{1}{\mu }} \\ \end{array} }} \right],\end{aligned}$$

(41)

$$\begin{aligned} \left( {\mathbf{B}+\mu \mathbf{I}} \right)^{-2}&= \left[ {{\begin{array}{ll} {\frac{1}{\left( {b+\mu } \right)^{2}}}&\\&{\frac{1}{\mu ^{2}}} \\ \end{array} }} \right]. \end{aligned}$$

(42)

On substituting (41) and (42) into (39) and (40), we have

$$\begin{aligned} \frac{1}{u_k}\frac{\mu m^{H}m+\left( b+\mu \right)n^{H}n}{\left( {b+\mu } \right)\mu }&= -\frac{2}{\lambda },\end{aligned}$$

(43)

$$\begin{aligned} \frac{1}{u_k }\frac{\mu ^{2}m^{H}m+\left( {b+\mu } \right)^{2}n^{H}n}{\left( {b+\mu } \right)^{2}\mu ^{2}}&= \frac{4P_k }{\lambda ^{2}}. \end{aligned}$$

(44)

From (43) and (44), we have

$$\begin{aligned} \frac{\mu ^{2}m^{H}m+\left( {\text{ b}+\mu } \right)^{2}n^{H}n}{\left( {b+\mu } \right)^{2}\mu ^{2}}=\frac{P_k }{u_k}\frac{\left( {\mu m^{H}m+\left( {b+\mu } \right)n^{H}n} \right)^{2}}{\left( {b+\mu } \right)^{2}\mu ^{2}}, \end{aligned}$$

(45)

and we can equivalently rewrite (45) as

$$\begin{aligned} \!\left[\!{\left( {e\!+\!f} \right)\left( {\frac{P_k }{u_k }\left( {e\!+\!f} \right)-1} \right)} \!\right]\mu ^{2}\!+\!\left[ {2bf\left( {\frac{P_k }{u_k }\left( {e\!+\!f} \right)-1} \right)} \right]\mu \!+\!\left[ {b^{2}f\left( {\frac{P_k }{u_k }f\!-\!1} \right)} \right]=0,\nonumber \\ \end{aligned}$$

(46)

where $e=m^{H}m$ and $f=n^{H}n$ which all are constants.

Then, we can calculate the optimal beamforming vector by Eqs. (38), (39) and (46). $\square$