Skip to main content
SpringerLink
Log in

Differential Quadrature Amplitude Modulation and Relay Selection with Detect-and-Forward Cooperative Relaying

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

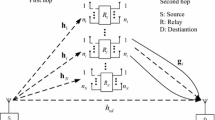
In this paper, we consider a cooperative communication system with differential modulation and relay-selection (DM–RS) in multi-relay networks, where the best relay is selected to forward the source node’s signal to the destination node with detect-and-forward (DetF) protocol. Unlike the conventional DM–RS–DetF scheme using phase shift keying (PSK), we propose a DM–RS–DetF scheme with quadrature amplitude modulation (QAM). Since the differential PSK scheme cannot be applied to the QAM constellations directly, we firstly develop the modulation and demodulation methods for the differential QAM scheme. Then, we derive a closed-form approximation and an upper bound of the symbol error rate for the DQAM–RS–DetF scheme over independent Rayleigh fading channels, by using the approximated signal-to-noise ratio of the equivalent relay link. Simulations results verify the validity of the analytical results and further show that when the modulation order \(M>8\) in Rayleigh fading channels, the DQAM–RS–DetF scheme outperforms the DPSK–RS–DetF scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. In [16], the proposed MLC is given by Eq. (8), i.e., \({{z}_{m}}\left( n \right) \approx y_{{ SD}}^{\text{* }}\left( n-1 \right) {{y}_{{ SD}}}\left( n \right) \text{+ }\frac{{{\gamma }_{eq}}}{{{\gamma }_{{ RD}}}}y_{{ RD}}^{\text{* }}\left( n-1 \right) {{y}_{{ RD}}}\left( n \right) \). If we consider a noise free situation, combining Eqs. (1), (2) and (5) in [16], we can obtain \({{z}_{m}}\left( n \right) \approx {{\mu }_{{ SD}}}d\left( n \right) +{{\mu }_{eq}}\tilde{d}\left( n \right) \), where \({{\mu }_{{ SD}}}={{\left| {{h}_{{ SD}}} \right| }^{2}}, {{\mu }_{eq}}=\min \{ {{\left| {{h}_{{ SR}}} \right| }^{2}}, {{\left| {{h}_{{ RD}}} \right| }^{2}} \}\). This is the MLC we used in this paper.

References

  1. Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part I. System description. IEEE Transactions on Communications, 51(11), 1927–1938.

    Article  Google Scholar 

  2. Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part II. Implementation aspects and performance analysis. IEEE Transactions on Communications, 51(11), 1939–1948.

    Article  Google Scholar 

  3. Nosratinia, A., Hunter, T., & Hedayat, A. (2004). Cooperative communication in wireless networks. IEEE Communications Magazine, 42(10), 74–80.

    Article  Google Scholar 

  4. Yang, Y., Hu, H., Xu, J., & Mao, G. (2009). Relay technologies for WiMax and LTE-advanced mobile systems. IEEE Communications Magazine, 47(10), 100–105.

    Article  Google Scholar 

  5. Laneman, J. N., Tse, D. N. C., & Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50(12), 3062–3080.

    Article  MathSciNet  Google Scholar 

  6. Bletsas, A., Khisti, A., Reed, D. P., & Lippman, A. (2006). A simple cooperative diversity method based on network path selection. IEEE Journal on Selected Areas in Communications, 24(3), 659–672.

    Article  Google Scholar 

  7. Ibrahim, A. S., Sadek, A. K., Su, W., & Liu, K. J. R. (2008). Cooperative communications with relay-selection: When to cooperate and whom to cooperate with. IEEE Transactions on Wireless Communications, 7(7), 2814–2827.

    Article  Google Scholar 

  8. Madan, R., Mehta, N., Molisch, A., & Zhang, J. (2008). Energy-efficient cooperative relaying over fading channels with simple relay selection. IEEE Transactions on Wireless Communication, 7(8), 3013–3025.

    Article  Google Scholar 

  9. Laneman, J. N., & Wornell, G. W. (2003). Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory, 49(10), 2415–2425.

    Article  MathSciNet  Google Scholar 

  10. Jing, Y., & Hassibi, B. (2006). Distributed space-time coding in wireless relay networks. IEEE Transactions on Wireless Communication, 5(12), 3524–3536.

    Article  Google Scholar 

  11. Jing, Y., & Jafarkhani, H. (2007). Using orthogonal and quasi-orthogonal designs in wireless relay networks. IEEE Transactions on Information Theory, 53(11), 4106–4118.

    Article  MathSciNet  Google Scholar 

  12. Zhao, Y., Adve, R., & Lim, T. J. (2007). Improving amplify-and-forward relay networks: Optimal power allocation versus selection. IEEE Transactions on Wireless Communications, 6(8), 3114–3123.

    Google Scholar 

  13. Jing, Y., & Jafarkhani, H. (2009). Single and multiple relay selection schemes and their achievable diversity orders. IEEE Transactions on Wireless Communications, 8(3), 1414–1423.

    Article  Google Scholar 

  14. Zheng, Z., Fu, S., Lu, K., Wang, J., & Chen, B. (2012). On the relay selection for cooperative wireless networks with physical-layer network coding. Wireless Networks, 18(6): 653–665.

    Google Scholar 

  15. Zhu, Y., Kam, P. Y., & Xin, Y. (2010). Differential modulation for decode-and-forward multiple relay systems. IEEE Transactions on Communications, 58(1), 189–199.

    Article  Google Scholar 

  16. Yuan, J., Li, Y., & Chu, L. (2010). Differential modulation and relay selection with detect-and-forward cooperative relaying. IEEE Transactions on Vehicle Technology, 59(1), 261–268.

    Article  Google Scholar 

  17. Gao, Y., Ge, J., & Han, C. (2011). Performance analysis of differential modulation and relay selection with detect-and-forward cooperative relaying. IEEE Communication Letters, 15(3), 323–325.

    Article  Google Scholar 

  18. Benjillali, M., & Szczecinski, L. (2009). A simple detect-and-forward scheme in fading channels. IEEE Communication Letters, 13(5), 309–311.

    Article  Google Scholar 

  19. Proakis, J. G. (2001). Digital communications (4th ed.). New York: McGraw-Hill.

    Google Scholar 

  20. Weber, W. I. I. I. (1978). Differential encoding for multiple amplitude and phase shift keying systems. IEEE Transactions on Communication, 26(3), 385–391.

    Article  Google Scholar 

  21. Warrier, D., & Madhow, U. (2002). Spectrally efficient noncoherent communication. IEEE Transaction on Information Theory, 48(3), 651–668.

    Article  MathSciNet  MATH  Google Scholar 

  22. Wang, T., Cano, A., Giannakis, G. B., & Laneman, N. (2007). High-performance cooperative demodulation with decode-and-forward relays. IEEE Transaction on Communications, 55(7), 1427–1438.

    Article  Google Scholar 

  23. David, H. A. (1970). Order statistics. Hoboken, NJ: Wiley.

    MATH  Google Scholar 

  24. Simon, M. K., & Alouini, M. S. (2005). Digital communications over fading channels (2nd ed.). Hoboken, NJ: Wiley.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an, China

    Yang Gao & Jianhua Ge

  2. School of Science, Xi’an University of Posts and Telecommunications, Xi’an, China

    Weijie Cong

Authors
  1. Yang Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jianhua Ge
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weijie Cong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yang Gao.

Additional information

This work was supported by the Fundamental Research Funds for the Central Universities (Grant No. K50511010005), the National Basic Research Program of China under Grant 2012CB316100, the 111 project (Grant No. B08038) and the National Natural Science Foundation of China (Grant Nos. 61001128, 61001207, 61101144 and 61101145). The authors gratefully acknowledge the Research in Motion (RIM) Corporation of Canada for financial support.

Appendix

Appendix

In this appendix, we will calculate the MSE of the CP estimation, i.e., Eq. (20) in Sect. 3. From the definition of the MSE,

$$\begin{aligned} {{ MSE}_{ CP}}&= E\left[ {{\left| P{{\left| h \right| }^{2}}-\frac{1}{L}{\mathbf{y }^{H}}\mathbf y \right| }^{2}} \right] \nonumber \\&= {{P}^{2}}E\left[ {{\left| h \right| }^{4}} \right] -\frac{2P}{L}E\left[ {{\left| h \right| }^{2}}{\mathbf{y }^{H}}\mathbf y \right] +\frac{1}{{{L}^{2}}}E\left[ {{\left( {\mathbf{y }^{H}}\mathbf y \right) }^{2}} \right] . \end{aligned}$$
(39)

Since \(h\sim { CN}\left( 0,\sigma _{h}^{2} \right) \), we have \(E\left[ {{\left| h \right| }^{4}} \right] =2\sigma _{h}^{2}\). Thus, the first term in (39) can be rewritten as

$$\begin{aligned} {{P}^{2}}E\left[ {{\left| h \right| }^{4}} \right] =2{{P}^{2}}\sigma _{h}^{2}. \end{aligned}$$
(40)

Using \(E[ {\mathbf{y }^{H}}\mathbf y ]=L{{\left| h \right| }^{2}} +L\sigma _{e}^{2}\), the second term in (39) becomes

$$\begin{aligned} \frac{2P}{L}E\left[ {{\left| h \right| }^{2}}{\mathbf{y }^{H}}\mathbf y \right]&= \frac{2P}{L}{E_{h}}\left[ {{\left| h\right| }^{2}}{E_\mathbf{x ,\mathbf e }}\left[ {\mathbf{y }^{H}}\mathbf y \right] \right] \nonumber \\&= \frac{2P}{L}{E_{h}}\left[ {{\left| h \right| }^{2}}\left( L{{\left| h \right| }^{2}} +L\sigma _{e}^{2} \right) \right] \nonumber \\&= 4{{P}^{2}}\sigma _{h}^{2}+2P\sigma _{h}^{2}\sigma _{e}^{2}. \end{aligned}$$
(41)

In addition, using (18), the third term in (39) can be expanded as

$$\begin{aligned} \frac{1}{{{L}^{2}}}E\left[ {{\left( {\mathbf{y }^{H}}\mathbf y \right) }^{2}} \right]&= \frac{1}{{{L}^{2}}}E\left[ {{\left( P{{\left| h \right| }^{2}}{\mathbf{x }^{H}}\mathbf x +2\sqrt{P}\mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) +{\mathbf{e }^{H}}\mathbf e \right) }^{2}} \right] \nonumber \\&= \frac{1}{{{L}^{2}}}E\left[ {{\left( P{{\left| h \right| }^{2}}{\mathbf{x }^{H}}\mathbf x \right) }^{2}} \right] +\frac{1}{{{L}^{2}}}E\left[ {{\left( 2\sqrt{P}\mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) +{\mathbf{e }^{H}}\mathbf e \right) }^{2}} \right] \nonumber \\&+\frac{2}{{{L}^{2}}}E\left[ P{{\left| h \right| }^{2}}{\mathbf{x }^{H}}\mathbf x \left( 2\sqrt{P}\mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) +{\mathbf{e }^{H}}\mathbf e \right) \right] \nonumber \\&= \frac{{{P}^{2}}}{{{L}^{2}}}E\left[ {{\left| h \right| }^{4}} \right] E\left[ {{\left( {\mathbf{x }^{H}}\mathbf x \right) }^{2}} \right] +\frac{4P}{{{L}^{2}}}E\left[ \mathfrak R {{\left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) }^{2}} \right] +\frac{1}{{{L}^{2}}}E\left[ {{\left( {\mathbf{e }^{H}}\mathbf e \right) }^{2}} \right] \nonumber \\&+\frac{4\sqrt{P}}{{{L}^{2}}}E\left[ \mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) {\mathbf{e }^{H}}\mathbf e \right] +\frac{4P\sqrt{P}}{{{L}^{2}}}E\left[ {{\left| h \right| }^{2}}{\mathbf{x }^{H}}\mathbf x \mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) \right] \nonumber \\&+\frac{2P}{{{L}^{2}}}E\left[ {{\left| h \right| }^{2}} \right] E\left[ {\mathbf{x }^{H}}\mathbf x \right] E\left[ {\mathbf{e }^{H}}\mathbf e \right] \nonumber \\&\triangleq {{ MSE}_{ CP1}}+{{ MSE}_{{ CP}2}}+{{ MSE}_{{ CP}3}}+{{ MSE}_{{ CP}4}}\nonumber \\&+{{ MSE}_{{ CP}5}} +{{ MSE}_{{ CP}6}}. \end{aligned}$$
(42)

Since the source symbols \({{s}_{1}},\ldots ,{{s}_{L}}\) are iid discrete random variables with \(E\left[ {{\left| {{s}_{l}} \right| }^{2}} \right] =1\), from (2) the first term in (42) can be calculated as

$$\begin{aligned} {{ MSE}_{{ CP}1}}&= \frac{{{P}^{2}}}{{{L}^{2}}}\times 2\sigma _{h}^{4}\times E\left[ {{\left( \sum \limits _{l=1}^{L}{{a}_{l}^2} \right) }^{2}} \right] \nonumber \\&= \frac{{{P}^{2}}}{{{L}^{2}}}\times 2\sigma _{h}^{4}\times \left( \sum \limits _{l=1}^{L}{E\left[ {a}_{l}^4\right] } +\sum \limits _{l=1}^{L}{\sum \limits _{k=1,k\ne l}^{L}{E\left[ {a}_{l}^2 \right] E\left[ {a}_{k}^2 \right] }}\right) \nonumber \\&= \frac{{{P}^{2}}}{{{L}^{2}}}\times 2\sigma _{h}^{4}\times \left[ {{L}^{2}}+L\left( {{\nu }_{a}}-1 \right) \right] \nonumber \\&= 2{{P}^{2}}\sigma _{h}^{4}+\frac{2{{P}^{2}}}{L}\left( {{\nu }_{a}}-1 \right) \sigma _{h}^{4}, \end{aligned}$$
(43)

where \({{\nu }_{a}}=E\left[ {a}_{l}^4 \right] \). Using \(\mathfrak R \left( {{h}^{*}}{\mathbf{x }^{H}}\mathbf e \right) =\mathfrak R \left( {{h}^{*}} \right) \sum \nolimits _{k=1}^{L}\mathfrak{R \left( x_{k}^{*}e \right) }+\mathfrak I \left( {{h}^{*}} \right) \sum \nolimits _{k=1}^{L}\mathfrak{I \left( x_{k}^{*}e \right) }\), the \({{{ MSE}}_{{ CP}2}}\) in (42) becomes

$$\begin{aligned} {{{ MSE}}_{{ CP}2}}&= \frac{4P}{{{L}^{2}}}\left\{ E\left[ \mathfrak R {{\left( {{h}^{*}} \right) }^{2}} \right] E\left[ \sum \limits _{k=1}^{L}\mathfrak{R {{\left( x_{k}^{*}{{e}_{k}} \right) }^{2}}} \right] +E\left[ \mathfrak I {{\left( {{h}^{*}} \right) }^{2}} \right] E\left[ \sum \limits _{k=1}^{L}\mathfrak{I {{\left( x_{k}^{*}{{e}_{k}} \right) }^{2}}} \right] \right\} \nonumber \\&= \frac{4P}{{{L}^{2}}}\times \left( \frac{1}{2}\sigma _{h}^{2}\times \frac{L}{2}\sigma _{e}^{2}+\frac{1}{2}\sigma _{h}^{2}\times \frac{L}{2}\sigma _{e}^{2} \right) \nonumber \\&= \frac{2P}{L}\sigma _{h}^{2}\sigma _{e}^{2} \end{aligned}$$
(44)

Moreover, \({\mathbf{e }^{H}}\mathbf e =\sum \nolimits _{k=1}^{L}{\left( \mathfrak R {{\left( {{e}_{k}} \right) }^{2}}+\mathfrak I {{\left( {{e}_{k}} \right) }^{2}} \right) }\) confines the central Chi-square distribution with \(2L\) degrees of freedom, then \(E\left[ {{\left( {\mathbf{e }^{H}}\mathbf e \right) }^{2}} \right] =\left( L+{{L}^{2}} \right) \sigma _{e}^{4}\). Thus, the \({{MSE}_{CP3}}\) in (42) can be obtained as

$$\begin{aligned} { MSE}_{{ CP}3}=\left( \frac{1}{L}+1 \right) \sigma _{e}^{4}. \end{aligned}$$
(45)

Since \(E\left[ \mathfrak R \left( {{h}^{*}} \right) \right] =E\left[ \mathfrak I \left( {{h}^{*}} \right) \right] =0\), the \({ MSE}_{{ CP}4}\) and \({ MSE}_{CP5}\) are equal to zero. In addition, the \({{{ MSE}}_{{ CP}6}}\) in (42) can be calculated as

$$\begin{aligned} {{{ MSE}}_{{ CP}6}}=2P\sigma _{h}^{2}\sigma _{e}^{2}. \end{aligned}$$
(46)

Substituting (43)–(46) into (42), the MSE of the CP estimation can be obtained as

$$\begin{aligned} {{{ MSE}}_{{ CP}}}=\frac{2{{P}^{2}}}{L}\sigma _{h}^{2}\left( {{\nu }_{a}}-1 \right) +\frac{2P}{L}\sigma _{h}^{2}\sigma _{e}^{2}+\left( \frac{1}{L}+1 \right) \sigma _{e}^{4}. \end{aligned}$$
(47)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gao, Y., Ge, J. & Cong, W. Differential Quadrature Amplitude Modulation and Relay Selection with Detect-and-Forward Cooperative Relaying. Wireless Pers Commun 72, 1399–1414 (2013). https://doi.org/10.1007/s11277-013-1085-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-013-1085-0

Keywords

Search

Navigation