Exact Outage Probability of a Decode-and-Forward Scheme with Best Relay Selection Under Physical Layer Security

Abstract

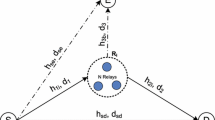
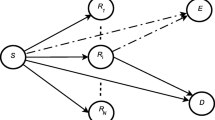
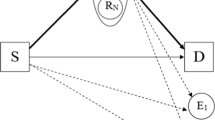
As demand for highly reliable data transmission in wireless networks has increased rapidly, cooperative communication technology has attracted a great deal of attention. In cooperative communication, some nodes, called eavesdroppers, illegally receive information that is intended for other communication links at the physical layer because of the broadcast characteristics of the wireless environment. Hence, Physical Layer Security is proposed to secure the communication link between two nodes against access by the eavesdroppers. In this paper, we propose and analyze the performance of decode-and-forward schemes with the best relay selection under Physical Layer Security with two operation protocols: first, only cooperative communication, and second, a combination of direct transmission and cooperative communication (the incremental protocol). In these schemes, a source transmits data to a destination with the assistance of relays, and the source-destination link is eavesdropped by one other node. The best relay is chosen in these proposals based on the maximum Signal-to-Noise ratio from the relays to the destination, and satisfies the secure communication conditions. The performance of each system is evaluated by the exact outage probability of the data rate over Rayleigh fading channels. Monte-Carlo results are presented to verify the theoretical analysis and are compared with a direct transmission scheme under Physical Layer Security and compared with each other.

Appendices

Appendix A: Solving the Probability $\Pr \left[ {D_2 =\left\{ \varnothing \right\} } \right]$ in Formula (19)

Substituting (9) and (10) into (19), we obtain (36) as

$$\begin{aligned} \Pr \left[ {D_2 =\left\{ \varnothing \right\} } \right] =\Pr \left[ {\gamma _{21} \le \gamma _{31} , \gamma _{22} \le \gamma _{32} , \ldots , \gamma _{2M} \le \gamma _{3M} } \right] =\prod _{i=1}^M {\Pr \left[ {\gamma _{2i} \le \gamma _{3i} } \right] }\quad \end{aligned}$$

(36)

The probability $\Pr \left[ {\gamma _{2i} <\gamma _{3i} } \right]$ is given as

$$\begin{aligned} \Pr \left[ {\gamma _{2i} <\gamma _{3i} } \right]&= \int \limits _{0}^\infty {\int \limits _0^x {f_{3i} (x)f_{2i} (y)dydx} } =\int \limits _0^\infty {\lambda _3 e^{-\lambda _3 x}F_{2i} (x)dx} \nonumber \\&= \int \limits _0^\infty {\lambda _3 e^{-\lambda _3 x}\left( {1-e^{-\lambda _2 x}} \right) dx=\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \end{aligned}$$

(37)

where $f_{2i} (\cdot ), f_{3i} (\cdot )$ and $F_{2i} (\cdot )$ are the probability density functions (PDF) of the exponential random variables $\gamma _{2i} , \gamma _{3i}$ and the CDF of the exponential random variable $\gamma _{2i}$, respectively, and given as

$$\begin{aligned} f_{2i} (x)=\lambda _{2} e^{-\lambda _2 x}\end{aligned}$$

(38)

$$\begin{aligned} f_{3i} (x)=\lambda _3 e^{-\lambda _3 x}\end{aligned}$$

(39)

$$\begin{aligned} F_{2i} (x)=1-e^{-\lambda _2 x} \end{aligned}$$

(40)

From (37), the probability $\Pr \left[ {D_2 =\left\{ \varnothing \right\} } \right]$ in (36) is obtained as

$$\begin{aligned} \Pr \left[ {D_2 =\left\{ \varnothing \right\} } \right] =\left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \right) ^{M} \end{aligned}$$

(41)

Appendix B: Solving the Probability in (24)

We note that there are $C_M^{K}$ possible ways for the subset $D_{2}$. Hence, formula (24) is expressed as

$$\begin{aligned} \Delta =\sum _{K=1}^M {C_M^K \Pr \left[ {\begin{array}{l} ASR_1 >0, ASR_2 >0, \ldots , ASR_K >0,ASR_{K+1} \le 0, ASR_{K+2}\\ \quad \le 0, \ldots , ASR_M \le 0, \\ R_{21} <R_P , R_{22} <R_P, \ldots , R_{2K} <R_P \nonumber \\ \end{array}} \right] }\\ \end{aligned}$$

(42)

Substituting (17) and (9) into (42), we obtain (43) as

$$\begin{aligned} \displaystyle \Delta&= \displaystyle \sum _{K=1}^M {C_M^K \Pr \left[ {\begin{array}{l} \gamma _{21} >\gamma _{31} , \gamma _{22} >\gamma _{32}, \ldots , \gamma _{2K} >\gamma _{3K} , \nonumber \\ \gamma _{2(K+1)} <\gamma _{3(K+1)} ,\gamma _{2(K+2)} <\gamma _{3(K+2)}, \ldots , \gamma _{2M} <\gamma _{3M} \\ \gamma _{21} <\theta , \gamma _{22} <\theta , \ldots , \gamma _{2K} <\theta \\ \end{array}} \right] } \nonumber \\ \displaystyle&= \displaystyle \sum _{K=1}^M {C_M^K \left\{ {\begin{array}{l} \Pr \left[ {\gamma _{2(K+1)} <\gamma _{3(K+1)} ,\gamma _{2(K+2)} <\gamma _{3(K+2)}, \ldots , \gamma _{2M} <\gamma _{3M} } \right] \nonumber \\ \times \Pr \left[ {\gamma _{31} <\gamma _{21} <\theta , \gamma _{32} < \gamma _{22} <\theta , \ldots , \gamma _{3K} <\gamma _{2K} <\theta } \right] \\ \end{array}} \right\} } \\ \displaystyle&= \displaystyle \sum _{K=1}^M {C_M^K \left\{ {\prod _{i=1}^K {\Pr \left[ {\gamma _{3i} <\gamma _{2i} <\theta } \right] } \prod _{j=K+1}^M {\Pr } \left[ {\gamma _{2j} <\gamma _{3j} } \right] } \right\} } \end{aligned}$$

(43)

The probability $\Pr \left[ {\gamma _{3i} <\gamma _{2i} <\theta } \right]$ is derived as

$$\begin{aligned}&\displaystyle \Pr \left[ {\gamma _{3i} <\gamma _{2i} <\theta } \right] =\int \limits _0^\theta {f_{3i} (x)\int \limits _x^\theta {f_{2i} (y)dydx} } =\int \limits _0^\theta {\lambda _3 e^{-\lambda _3 x}\left[ {F_{2i} (\theta )-F_{2i} (x)} \right] dx} \nonumber \\&\quad \displaystyle =\int \limits _0^\theta {\lambda _3 e^{-\lambda _3 x}\left[ {e^{-\lambda _2 x}-e^{-\lambda _2 \theta }} \right] dx} =\frac{\lambda _3 }{\lambda _2 +\lambda _3 }+\frac{\lambda _2 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) }-e^{-\lambda _2 \theta } \end{aligned}$$

(44)

where $f_{2i} (\cdot ), f_{3i} (\cdot )$and $F_{2i} (\cdot )$ are given in (38), (39) and (40) in “Appendix A”, respectively.

Substituting (37) and (44) into (43), we have the probability $\Delta$ in (24) as

$$\begin{aligned} \displaystyle \Delta&= \displaystyle \sum _{K=1}^M {C_M^K \left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \right) ^{M-K}\left[ {\frac{\lambda _3 }{\lambda _2 +\lambda _3 }+\frac{\lambda _2 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) }-e^{-\lambda _2 \theta }} \right] ^{K}} \nonumber \\ \displaystyle&= \displaystyle \left( {1+\frac{\lambda _2 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) }-e^{-\lambda _2 \theta }} \right) ^{M}-\left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \right) ^{M} \end{aligned}$$

(45)

Appendix C: Solving the Probability in (28)

Similar to “Appendix B”, there are $C_M^K$ possible ways for the subset $D_{2}$. Hence, formula (28) is expressed as

$$\begin{aligned} \Omega =\sum _{K=1}^M {C_M^K \Pr \left[ {\begin{array}{l} ASR_1 >0, ASR_2 >0, \ldots , ASR_K >0,ASR_{K+1} \le 0, ASR_{K+2}\\ \quad \le 0,\ldots , ASR_M \le 0, \\ R_{31} >R_P , R_{32} >R_P, \ldots , R_{3K} >R_P \\ \end{array}} \right] }\nonumber \\ \end{aligned}$$

(46)

Substituting (17) and (10) into (46), formula (47) is obtained as

$$\begin{aligned} \displaystyle \Omega&= \sum _{K=1}^M {C_M^K \Pr \left[ {\begin{array}{l} \gamma _{21} >\gamma _{31} , \gamma _{22} >\gamma _{32}, \ldots , \gamma _{2K} >\gamma _{3K} , \nonumber \\ \displaystyle \gamma _{2(K+1)} <\gamma _{3(K+1)} ,\gamma _{2(K+2)} <\gamma _{3(K+2)}, \ldots , \gamma _{2M} <\gamma _{3M} \nonumber \\ \gamma _{31} >\theta , \gamma _{32} >\theta , \ldots , \gamma _{3K} >\theta \nonumber \\ \end{array}} \right] } \nonumber \\ \displaystyle&= \sum _{K=1}^M {C_M^K \left\{ {\begin{array}{l} \Pr \left[ {\gamma _{2(K+1)} <\gamma _{3(K+1)} ,\gamma _{2(K+2)} <\gamma _{3(K+2)}, \ldots , \gamma _{2M} <\gamma _{3M} } \right] \nonumber \\ \times \Pr \left[ {\gamma _{21} >\gamma _{31} >\theta , \gamma _{22} > \gamma _{32} >\theta , \ldots , \gamma _{2K} >\gamma _{3K} >\theta } \right] \nonumber \\ \end{array}} \right\} }\nonumber \\ \displaystyle&= \sum _{K=1}^M {C_M^K \left\{ {\prod _{i=1}^K {\Pr \left[ {\gamma _{2i} >\gamma _{3i} >\theta } \right] } \prod _{j=K+1}^M {\Pr } \left[ {\gamma _{2j} <\gamma _{3j} } \right] } \right\} } \end{aligned}$$

(47)

The probability $\Pr \left[ {\gamma _{2i} >\gamma _{3i} >\theta } \right]$ is derived as

$$\begin{aligned} \displaystyle \Pr \left[ {\gamma _{2i} >\gamma _{3i} >\theta } \right]&= \displaystyle \int \limits _\theta ^\infty {f_{2i} (x)\int _\theta ^x {f_{3i} (y)dydx} } =\int \limits _\theta ^\infty {\lambda _2 e^{-\lambda _2 x}\left[ {F_{3i} (x)-F_{3i} (\theta )} \right] dx}\nonumber \\ \displaystyle&= \displaystyle \int \limits _\theta ^\infty {\lambda _2 e^{-\lambda _2 x}\left[ {e^{-\lambda _3 \theta }-e^{-\lambda _3 x}} \right] dx} =\frac{\lambda _3 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) } \end{aligned}$$

(48)

where $f_{2i} (\cdot )$ and $f_{3i} (\cdot )$ are given in (38) and (39) in “Appendix A”, respectively; $F_{3i} (\cdot )$ is the CDF of the exponential random variable $\gamma _{3i}$, and given as

$$\begin{aligned} F_{3i} (x)=1-e^{-\lambda _3 x} \end{aligned}$$

(49)

Substituting (37) and (48) into (47), we have the probability $\Omega$ in (28) as

$$\begin{aligned} \Omega&= \sum _{K=1}^M {C_M^K \left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \right) ^{M-K}\left[ {\frac{\lambda _3 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) }} \right] ^{K}}\nonumber \\&= \left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }+\frac{\lambda _3 }{\lambda _2 +\lambda _3 }e^{-\theta \left( {\lambda _2 +\lambda _3 } \right) }} \right) ^{M}-\left( {\frac{\lambda _2 }{\lambda _2 +\lambda _3 }} \right) ^{M} \end{aligned}$$

(50)