Adaptive Cooperative Decode-and-Forward Transmission with Power Allocation Under Interference Constraint

Abstract

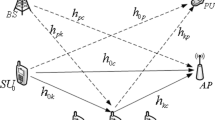
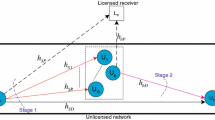
In this paper, we examine an adaptive decode-and-forward cooperative protocol under interference constraint. In the proposed protocol, relying on the obtained instantaneous signal-to-noise ratios (SNRs), a direct link or relay link is used to transmit data from the secondary source to the secondary destination. In addition, once the relay link is used, the secondary source and relay must adapt their transmit power to maximize the instantaneous SNR of this link. To evaluate the performance of the proposed protocol, we derive closed-form lower-bound and upper-bound expressions for the outage probability over Rayleigh fading channel. Finally, various Monte-Carlo simulations are presented to verify our analysis and compare the performance of the proposed protocol with that of the direct transmission protocol in underlay cognitive network.

Appendices

Appendix A

1.1 Proof of (4)

For ease of presentation, we set $y=P_{S}^{CC}$ and from (2), we have $P_{R}^{CC} =\frac{I_{P} }{\gamma _{3} }-y$. Hence, the optimization problem can be formulated as follows:

$$\begin{aligned}&\mathop {\max }\limits _{y} f(y)=\min \left( {y\gamma _{1}, \left( {\frac{I_{P} }{\gamma _{3} }-y} \right) \gamma _{2} } \right) \end{aligned}$$

(13)

$$\begin{aligned}&\text{ s.t.: }\quad \text{ s.t.: } 0<y\le \frac{I_{P} }{\gamma _{3}},\quad \text{ and } \end{aligned}$$

(14)

$$\begin{aligned}&\frac{I_{P} }{\gamma _{3} }-\frac{I_{P} }{\gamma _{4} }\le y \end{aligned}$$

(15)

where constraints (14) and (15) are obtained by $P_{S}^{\textit{CC}} \le I_{P} /\gamma _{3}$ and $P_{R}^{\textit{CC}} \le I_{P} /\gamma _{4}$, respectively.

Next, we consider three cases as follows:

Case 1::

$\frac{\gamma _{3} }{\gamma _{4} }\ge 1$

In this case, the constraint (15) is omitted and the function $f\left( y \right)$ obtains the optimal value, i.e., $f_{\max } \left( y \right) =\frac{I_{P} \gamma _{1} \gamma _{2} }{\left( {\gamma _{1} +\gamma _{2} } \right) \gamma _{3} }$, as $y\gamma _{1} =\left( {\frac{I_{P} }{\gamma _{3} }-y} \right) \gamma _{2}$ or $y=\frac{I_{P} \gamma _{2} }{\left( {\gamma _{1} +\gamma _{2} } \right) \gamma _{3} }$.

Case 2::

$\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\le \frac{\gamma _{3} }{\gamma _{4} }<1$

In this case, because $\frac{I_{P} }{\gamma _{3} }-\frac{I_{P} }{\gamma _{4} }\le \frac{I_{P} \gamma _{2} }{\left( {\gamma _{1} +\gamma _{2} } \right) \gamma _{3} }$, similar to Case 1, the optimal value of $f\left( y \right)$ is $f_{\max } \left( y \right) =I_{P} \frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }$ when $y=I_{P} \frac{\gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }$.

Case 3::

$\frac{\gamma _{3} }{\gamma _{4} }<\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }$

In this case, because $\frac{I_{P} }{\gamma _{3} }-\frac{I_{P} }{\gamma _{4} }>\frac{I_{P} \gamma _{2} }{\left( {\gamma _{1} +\gamma _{2} } \right) \gamma _{3} }$, so $y\gamma _{1} >\left( {\frac{I_{P} }{\gamma _{3} }-y} \right) \gamma _{2}$ and $f\left( y \right) =\left( {\frac{I_{P} }{\gamma _{3} }-y} \right) \gamma _{2}$. Similar to Case 2, the function $f\left( y \right)$ obtains the optimal value $f_{\max } \left( y \right) =I_{P} \frac{\gamma _{2} }{\gamma _{4} }$ as $y=\frac{I_{P} }{\gamma _{3} }-\frac{I_{P} }{\gamma _{4} }$.

From results obtained in Case 1, Case 2 and Case 3, the optimal solution $f_{\max } \left( y \right)$ can be given as follows:

$$\begin{aligned} f_{\max } \left( y \right) =\left\{ {\begin{array}{ll} I_{P} \frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) } ;&{}\quad \text{ if }\quad \frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }<\frac{\gamma _{3} }{\gamma _{4} } \quad \text{ as }\quad y=\frac{I_{P} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }. \\ I_{P} \frac{\gamma _{2} }{\gamma _{4} };&{}\quad \text{ if }\quad \frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4} } \quad \text{ as }\quad y=\frac{I_{P} }{\gamma _{3} }-\frac{I_{P} }{\gamma _{4}}.\\ \end{array}} \right. \end{aligned}$$

(16)

From (16) and $\gamma _{\max }^{CC} =f_{\max } \left( y \right) /N_{0}$, we obtain (4).

Appendix B

1.1 Proof of (9)

Considering the probability $\Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }<\rho ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }<\frac{\gamma _{3} }{\gamma _{4} } ,\frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }<\rho } \right]$ in (8); applying the inequality $\frac{\gamma _{1} \gamma _{2} }{\gamma _{1} +\gamma _{2} }\le \min \left( {\gamma _{1}, \gamma _{2} } \right)$, it can be bounded as

$$\begin{aligned}&\Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }<\rho ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }<\frac{\gamma _{3} }{\gamma _{4} } ,\frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }<\rho } \right] \ge \nonumber \\&\quad \ge \Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }<\rho ,\min \left( {\gamma _{1} ,\gamma _{2} } \right) <\frac{\gamma _{2} \gamma _{3} }{\gamma _{4} } ,\min \left( {\gamma _{1} ,\gamma _{2} } \right) <\rho \gamma _{3} } \right] \\&\quad \ge \underbrace{\Pr \left[ {\gamma _{1} \ge \gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,\gamma _{4} <\gamma _{3} ,\gamma _{2} <\rho \gamma _{3} } \right] }_{J_1} \nonumber \\&\qquad +\underbrace{\Pr \left[ {\gamma _{1} <\gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,\gamma _{4} \gamma _{1} <\gamma _{2} \gamma _{3} ,\gamma _{1} <\rho \gamma _{3} } \right] }_{J_2}\nonumber \end{aligned}$$

(17)

Considering the probability $J_{1}$ in (17), it can be formulated as

$$\begin{aligned} J_1&= \Pr \left[ {\gamma _{3} >\max \left( {\gamma _{4},\frac{\gamma _{0} }{\rho },\frac{\gamma _{2} }{\rho }} \right) ,\gamma _{1} \ge \gamma _{2} } \right] \nonumber \\&= \int \limits _{0}^{+\infty } {\lambda _{3} e^{-\lambda _{3} x}\Pr } \left[ {\max \left( {\gamma _{4} ,\frac{\gamma _{0} }{\rho },\frac{\gamma _{2} }{\rho }} \right) <x,\gamma _{1} \ge \gamma _{2} } \right] dx \end{aligned}$$

(18)

In (18), $\Pr \left[ {\max \left( {\gamma _{4} ,\frac{\gamma _{0} }{\rho },\frac{\gamma _{2} }{\rho }} \right) <x,\gamma _{1} \ge \gamma _{2} } \right]$ can be calculated as

$$\begin{aligned}&\Pr \left[ {\max \left( {\gamma _{4} ,\frac{\gamma _{0} }{\rho },\frac{\gamma _{2} }{\rho }} \right) <x,\gamma _{1} \ge \gamma _{2} } \right] \nonumber \\&\quad = \Pr \left[ {\gamma _{4} \le x} \right] \Pr \left[ {\gamma _{0} \le \rho x} \right] \int \limits _{0}^{\rho x} {\lambda _{2} e^{-\lambda _{2} u}du} \int \limits _{u}^{+\infty } {\lambda _{1} e^{-\lambda _{1} v}dv} \nonumber \\&\quad =\frac{\lambda _{2} }{\lambda _{1} +\lambda _{2} }\left( {1-e^{-\lambda _{4} x}} \right) \left( {1-e^{-\lambda _{0} \rho x}} \right) \left( {1-e^{-\left( {\lambda _{1} +\lambda _{2} } \right) \rho x}} \right) \end{aligned}$$

(19)

Substituting (19) into (18) and after some simple manipulation, we get

$$\begin{aligned} J_{1}&= \frac{\lambda _{2} \rho }{\lambda _{3} +\left( {\lambda _{1} +\lambda _{2} } \right) \rho }-\frac{\lambda _{2} \lambda _{3} \rho }{\left( {\lambda _{3} +\lambda _{4} } \right) \left[ {\lambda _{3} +\lambda _{4} +\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] } \nonumber \\&\quad -\frac{\lambda _{2} \lambda _{3} \rho }{\left( {\lambda _{3} +\lambda _{0} \rho } \right) \left[ {\lambda _{3} +\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho } \right] } \nonumber \\&\quad +\frac{\lambda _{2} \lambda _{3} \rho }{\left( {\lambda _{3} +\lambda _{4} +\lambda _{0} \rho } \right) \left[ {\lambda _{3} +\lambda _{4} +\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho } \right] } \end{aligned}$$

(20)

Now, considering the probability $J_{2}$ in (17), using the inequality $\gamma _{1} <\rho \gamma _{3}$, we have

$$\begin{aligned} J_{2}&= \Pr \left[ {\gamma _{1} <\gamma _{2} ,\gamma _{0} <\rho \gamma _{3}, \gamma _{1} \gamma _{4} <\gamma _{2} \gamma _{3} ,\gamma _{1} <\rho \gamma _{3} } \right] \nonumber \\&\ge \underbrace{\Pr \left[ {\gamma _{1} <\gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,\rho \gamma _{4} <\gamma _{2} ,\gamma _{1} <\rho \gamma _{3} } \right] }_{J_{3}} \end{aligned}$$

(21)

Similar to (18), we can formulate the probability $J_{3}$ in (21) as follows:

$$\begin{aligned} J_{3}&= \Pr \left[ {\gamma _{2} >\max \left( {\gamma _{1} ,\rho \gamma _{4} } \right) ,\gamma _{0} <\rho \gamma _{3} ,\gamma _{1} <\rho \gamma _{3} } \right] \nonumber \\&= \int \limits _{0}^{+\infty } {\left\{ {\lambda _{2} e^{-\lambda _{2} x}\Pr \left[ {\gamma _{4} \le \frac{x}{\rho }} \right] \int \limits _0^x {\lambda _{1} e^{-\lambda _{1} u}du} \int \limits _{\frac{u}{\rho }}^{+\infty } {\lambda _{3} e^{-\lambda _{3} v}dv} \int \limits _0^{\rho v} {\lambda _{0} e^{-\lambda _{0} t}dt} } \right\} dx} \end{aligned}$$

(22)

From (22) and after some manipulation, we obtain

$$\begin{aligned} J_3&= \frac{\lambda _{0} \lambda _{1} \lambda _{4} \rho ^{2}\left[ {2\lambda _{3} +\left( {\lambda _{0} +\lambda _{1} } \right) \rho } \right] }{\left( {\lambda _{3} +\lambda _{0} \rho } \right) \left( {\lambda _{3} +\lambda _{1} \rho } \right) \left( {\lambda _{4} +\lambda _{2} \rho } \right) \left[ {\lambda _{3} +\left( {\lambda _{0} +\lambda _{1} } \right) \rho } \right] } \nonumber \\&\quad -\frac{\lambda _{1} \lambda _{2} \lambda _{4} \rho ^{2}}{\left( {\lambda _{3} +\lambda _{1} \rho } \right) \left[ {\lambda _{3} +\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] \left[ {\lambda _{3} +\lambda _{4} \left( {\lambda _{0} +\lambda _{1} } \right) \rho } \right] } \nonumber \\&\quad +\frac{\lambda _{1} \lambda _{2} \lambda _{3} \lambda _{4} \rho ^{2}}{\left( {\lambda _{3} +\lambda _{0} \rho } \right) \left[ {\lambda _{3} +\left( {\lambda _{0} +\lambda _{1} } \right) \rho } \right] \left[ {\lambda _{3} +\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho } \right] }\nonumber \\&\times \frac{1}{\lambda _{3} +\lambda _{4} \left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho } \end{aligned}$$

(23)

Now, considering the probability $\Pr \left[ {\gamma _{0} <\rho \gamma _{3}, \frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4}}, \gamma _{2} \le \rho \gamma _{4} } \right]$ in (8); it can be rewritten as follows:

$$\begin{aligned}&\Pr \left[ {\gamma _{0} <\rho \gamma _{3} ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4}},\gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&\quad =\Pr \left[ {\gamma _{1} \ge \gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,\frac{\gamma _{1} +\gamma _{2} }{\gamma _{1} }\frac{\gamma _{3} }{\gamma _{4} }\le 1,\gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&\qquad +\Pr \left[ {\gamma _{1} <\gamma _{2} ,\gamma _{0} <\rho \gamma _{3},\frac{\gamma _{1} +\gamma _{2} }{\gamma _{1} }\frac{\gamma _{3} }{\gamma _{4} }\le 1,\gamma _{2} \le \rho \gamma _{4} } \right] \end{aligned}$$

(24)

With $\gamma _{1} \ge \gamma _{2}$, we have $\frac{\gamma _{1} +\gamma _{2} }{\gamma _{1} }\frac{\gamma _{3} }{\gamma _{4} }<\frac{2\gamma _{3} }{\gamma _{4} }$ and with $\gamma _{1} <\gamma _{2}$ and $\gamma _{2} \le \rho \gamma _{4}$, we obtain $\frac{\gamma _{1} +\gamma _{2} }{\gamma _{1} }\frac{\gamma _{3} }{\gamma _{4} }\le \frac{\gamma _{1} +\gamma _{2} }{\gamma _{1} \gamma _{2} }\rho \gamma _{3} \le \frac{2\rho \gamma _{3} }{\gamma _{1}}$. Hence, (24) can be bounded by

$$\begin{aligned}&\Pr \left[ {\gamma _{0} <\rho \gamma _{3} ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4}},\gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&\quad \ge \underbrace{\Pr \left[ {\gamma _{1} \ge \gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,2\gamma _{3} \le \gamma _{4} ,\gamma _{2} \le \rho \gamma _{4} } \right] }_{J_4 }\nonumber \\&\quad +\underbrace{\Pr \left[ {\gamma _{1} <\gamma _{2},\gamma _{0} <\rho \gamma _{3} ,2\rho \gamma _{3} \le \gamma _{1},\gamma _{2} \le \rho \gamma _{4} } \right] }_{J_{5}} \end{aligned}$$

(25)

Considering the probability $J_{4}$ in (25), it can be calculated as

$$\begin{aligned} J_{4}&= \Pr \left[ {\gamma _{2} \le \min \left( {\gamma _{1} ,\rho \gamma _{4} } \right) ,\frac{\gamma _{0} }{\rho }<\gamma _{3} <\frac{\gamma _{4} }{2}} \right] \nonumber \\&= \int \limits _0^{+\infty } {\left\{ {\lambda _{2} e^{-\lambda _{2} x}\Pr \left[ {\gamma _{1} \ge x} \right] \int \limits _{\frac{x}{\rho }}^{+\infty } {\lambda _{4} e^{-\lambda _{4} u}du} \int \limits _0^{\frac{u}{2}} {\lambda _{3} e^{-\lambda _{3} v}dv} \int \limits _0^{\rho v} {\lambda _{0} e^{-\lambda _{0} t}dt} } \right\} dx} \nonumber \\&= \frac{\lambda _{0} \lambda _{2} \rho ^{2}}{\left( {\lambda _{3} +\lambda _{0} \rho } \right) \left[ {\lambda _{4} +\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] }-\frac{4\lambda _{2} \lambda _{4} \rho }{\left( {\lambda _{3} +2\lambda _{4} } \right) \left[ {\lambda _{3} +2\lambda _{4} +2\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] } \nonumber \\&\quad +\frac{4\lambda _{2} \lambda _{3} \lambda _{4} \rho }{\left( {\lambda _{3} +\lambda _{0} \rho } \right) \left( {\lambda _{3} +2\lambda _{4} +\lambda _{0} \rho } \right) \left[ {\lambda _{3} +2\lambda _{4} +\left( {\lambda _{0} +2\lambda _{1} +2\lambda _{2} } \right) \rho } \right] } \end{aligned}$$

(26)

Next, we calculate the probability $J_{5}$ in (25) as

$$\begin{aligned} J_{5}&= \Pr \left[ {\gamma _{1} <\gamma _{2} ,\gamma _{0} <\rho \gamma _{3} ,2\rho \gamma _{3} \le \gamma _{1} ,\gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&= \int \limits _0^{+\infty } {\lambda _{0} e^{-\lambda _{0} x}dx\int \limits _{\frac{x}{\rho }}^{+\infty } {\lambda _{3} e^{-\lambda _{3} y}dy} } \int \limits _{2\rho y}^{+\infty } {\lambda _{1} e^{-\lambda _{1} z}dz} \int \limits _z^{+\infty } {\lambda _{2} e^{-\lambda _{2} v}dv} \int \limits _{\frac{v}{\rho }}^{+\infty } {\lambda _{4} e^{-\lambda _{4} t}dt} \nonumber \\&= \frac{\lambda _{0} \lambda _{1} \lambda _{2} \lambda _{3} \rho ^{3}}{\left[ {\lambda _{4} +\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] \left[ {\lambda _{3} +2\lambda _{4} +2\left( {\lambda _{1} +\lambda _{2} } \right) \rho } \right] \left[ {\lambda _{4} +\lambda _{2} \rho } \right] }\nonumber \\&\times\;\frac{1}{\left[ {\lambda _{3} +2\lambda _{4} +\left( {\lambda _{0} +2\lambda _{1} +2\lambda _{2} } \right) \rho } \right] } \end{aligned}$$

(27)

From (8), (17), (21) and (25), the outage probability $P_{CC}^{out}$ can be bounded as

$$\begin{aligned} P_{CC}^{out} \ge J_{1} +J_{3} +J_{4} +J_{5} =P_{CC}^{LB} \end{aligned}$$

(28)

Hence, substituting the results in (20), (23), (26) and (27) into (28), we obtain (9).

Appendix C

1.1 Proof of (10)

Considering the probability $\Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }<\rho ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }<\frac{\gamma _{3} }{\gamma _{4}}, \frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }<\rho } \right]$ in (8); it can be bounded as

$$\begin{aligned} \Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }\!<\!\rho ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }<\frac{\gamma _{3} }{\gamma _{4}}, \frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }\!<\!\rho } \right] <\underbrace{\Pr \left[ {\frac{\gamma _{0} }{\gamma _{3} }\!<\!\rho , \frac{\gamma _{1} \gamma _{2} }{\gamma _{3} \left( {\gamma _{1} +\gamma _{2} } \right) }\!<\!\rho } \right] }_{I_{1}}\quad \end{aligned}$$

(29)

Setting $X=\frac{\gamma _{1} \gamma _{2} }{\gamma _{1} +\gamma _{2}}$, the CDF of $X$ is given as

$$\begin{aligned} F_X \left( x \right) =1-2\sqrt{\lambda _{1} \lambda _{2} }x \exp \left( {-\left( {\lambda _{1} +\lambda _{2} } \right) x} \right) K_1 \left( {2\sqrt{\lambda _{1} \lambda _{2} }x } \right) \end{aligned}$$

(30)

where $K_{1} \left( . \right)$ is modified Bessel Function of the second kind [20].

From (29) and (30), we can formulate $I_{1}$ as

$$\begin{aligned} I_{1} =\Pr \left[ {\gamma _{0} <\rho \gamma _{3}, \frac{\gamma _{1} \gamma _{2} }{\gamma _{1} +\gamma _{2} }<\rho \gamma _{3} } \right] =\int \limits _{0}^{+\infty } {f_{\gamma _{3} } \left( x \right) F_{\gamma _{0} } \left( {\rho x} \right) F_x \left( {\rho x} \right) } dx \end{aligned}$$

(31)

Now, we have the following integral:

$$\begin{aligned} \int \limits _{0}^{+\infty } {\alpha _{1} \exp \left( {-\alpha _{2} x} \right) K_{1} \left( {\alpha _{3} x} \right) } dx=\frac{\alpha _{1} \alpha _{2} }{\alpha _{3} \left( {\alpha _{2}^2 -\alpha _{3}^2 } \right) }-\frac{\alpha _{1} \alpha _{3} }{\left( {\alpha _{2}^{2} -\alpha _{3}^{2} } \right) ^{3/2}}\cosh ^{-1}\left( {\frac{\alpha _{2} }{\alpha _{3} }} \right) \end{aligned}$$

(32)

where $\alpha _{1}, \,\alpha _{2}$ and $\alpha _{3}$ are positive real numbers, and $\cosh ^{-1}\left( x \right)$ is inverse hyperbolic cosine, which is given as $\cosh ^{-1}\left( x \right) =\ln \left( {x+\sqrt{x^{2}-1}} \right)$.

Substituting the PDF $f_{\gamma _{3} } \left( x \right) =\lambda _{3} \exp \left( {-\lambda _{3} x} \right)$, the CDF $F_{\gamma _{0} } \left( {\rho x} \right) =1-\exp \left( {-\lambda _{0} \rho x} \right)$, the CDF $F_{x} \left( {\rho x} \right)$ obtained in (30) and the result obtained in (32) into (31), we obtain

$$\begin{aligned} I_1&= \frac{\lambda _{0} \rho }{\lambda _{0} \rho +\lambda _{3} }\!-\!\frac{\lambda _{3} \left[ {\left( {\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] }{\left[ {\left( {\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] ^{2}-4\lambda _{1} \lambda _{2} \rho ^{2}}+\frac{4\lambda _{1} \lambda _{2} \lambda _{3} \rho ^{2}\, \text{ arccosh }\,\left[ {\frac{\left( {\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} }{2\sqrt{\lambda _{1} \lambda _{2} }\rho }} \right] }{\left\{ {\left[ {\left( {\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] ^{2}-4\lambda _{1} \lambda _{2} \rho ^{2}} \right\} ^{3/2}} \nonumber \\&\quad \!+\!\frac{\lambda _{3} \left[ {\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] }{\left[ {\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] ^{2}-4\lambda _{1} \lambda _{2} \rho ^{2}}\!-\!\frac{4\lambda _{1} \lambda _{2} \lambda _{3} \rho ^{2}\, \text{ arccosh }\,\left[ {\frac{\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} }{2\sqrt{\lambda _{1} \lambda _{2} }\rho }} \right] }{\left\{ {\left[ {\left( {\lambda _{0} +\lambda _{1} +\lambda _{2} } \right) \rho +\lambda _{3} } \right] ^{2}-4\lambda _{1} \lambda _{2} \rho ^{2}} \right\} ^{3/2}}\nonumber \\ \end{aligned}$$

(33)

Similarly, the outage probability $\Pr \left[ {\gamma _{0} <\rho \gamma _{3}, \frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4} } ,\gamma _{2} \le \rho \gamma _{4} } \right]$ in (8) can be bounded as follows:

$$\begin{aligned}&\Pr \left[ {\gamma _{0} <\rho \gamma _{3} ,\frac{\gamma _{1} }{\gamma _{1} +\gamma _{2} }\ge \frac{\gamma _{3} }{\gamma _{4}}, \gamma _{2} \le \rho \gamma _{4} } \right] <\Pr \left[ {\gamma _{0} <\rho \gamma _{3}, \gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&\quad =\Pr \left[ {\gamma _{0} <\rho \gamma _{3} } \right] \Pr \left[ {\gamma _{2} \le \rho \gamma _{4} } \right] \nonumber \\&\quad <\frac{\lambda _{0} \lambda _{2} \rho ^{2}}{\left( {\lambda _{0} \rho +\lambda _{3} } \right) \left( {\lambda _{2} \rho +\lambda _{4} } \right) }. \end{aligned}$$

(34)

From (8), (29), (33) and (34), we have $P_{CC}^{out} <P_{CC}^{UB}$, where $P_{CC}^{UB}$ is given as in (10).