Switched-Diversity Approach for Cognitive Scheduling

Abstract

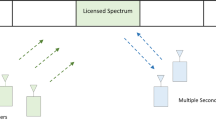
This article investigates the scheduling of secondary users in a spectrum-sharing cognitive environment under the primary user’s outage probability constraint. A switched-diversity combining approach to schedule the secondary users is explored. Specifically, switch-and-examine, switch-and-stay, selection-combining, and post-selection scheduling algorithms are investigated. Secondary users’ average performance measures are derived for the scheduling algorithms and compared against those of a single-user cognitive system. Results of this work illustrate the trade-off between the complexity of a scheduling algorithm and its average performance.

Appendices

Appendix 1: Derivation of Equation (7)

For $b > 0$ and $\mathrm{Q}{(x)} = \frac{1}{\sqrt{2 \pi }} \int _{x}^{\infty }{\exp {(-\frac{1}{2}y^2)}\,\mathrm{d}y}, A = \int \limits _{0}^{\infty } {\mathrm{Q}{(\sqrt{2 x})}\, \frac{b}{(x+b)^2} \,\mathrm{d}x}$ can be expressed as

$$\begin{aligned} A&= \int \limits _{0}^{\infty } {\int \limits _{\sqrt{2 x}}^{\infty }{\frac{1}{\sqrt{2 \pi }} \exp {(-\frac{1}{2}y^2)}\,\frac{b}{(x+b)^2} \,\mathrm{d}y} \,\mathrm{d}x} \\&= \frac{b}{\sqrt{2 \pi }} \int \limits _{0}^{\infty }{\exp {(-\frac{1}{2}y^2)} \int \limits _{0}^{\frac{1}{2}y^2}{\frac{1}{(x+b)^2} \,\mathrm{d}x} \,\mathrm{d}y} \\&= \frac{b}{\sqrt{2 \pi }} \int \limits _{0}^{\infty }{\exp {(-\frac{1}{2}y^2)} \left( \frac{1}{b}-\frac{1}{b + \frac{1}{2}y^2} \right) \,\mathrm{d}y}\\&= \frac{1}{2} - \frac{b}{\sqrt{2 \pi }} \int \limits _{0}^{\infty }{ \frac{\exp {(-\frac{1}{2}y^2)}}{b + \frac{1}{2}y^2}\,\mathrm{d}y}\\&\stackrel{(i)}{=} \frac{1}{2} - \frac{b}{\sqrt{\pi }} \int \limits _{0}^{\infty }{ \frac{\exp {(- t^2)}}{b + t^2}\,\mathrm{d}t} \\&\stackrel{(ii)}{=} \frac{1}{2} - \frac{b}{\sqrt{\pi }}\, \left( \frac{\pi }{2 \sqrt{b}} \,\exp {(b)}\, \mathrm{{erfc}}{(\sqrt{ b})}\right) \\&= \frac{1}{2} - \sqrt{\pi b}\, \exp {(b)}\, \mathrm{Q}{(\sqrt{2 b})}\,\cdot \end{aligned}$$

where $(i)$ is found by using $t^2 = \frac{1}{2}y^2$ and $(ii)$ is found from [14, Equation 7.4.11].

Appendix 2: Derivation of Equation (12)

For $a \ge 0$ and $b > 0, A = \int _{a}^{\infty } {\log _2{(1 + x)} \frac{b}{(x+b)^2} \,\mathrm{d}x}$ can be found for $b = 1$ as

$$\begin{aligned} A&= \int \limits _{a}^{\infty } {\log _2{(1 + x)} \frac{1}{(x + 1)^2} \,\mathrm{d}x} \\&= \int \limits _{a+1}^{\infty } {\log _2{(y)} \frac{1}{y^2} \,\mathrm{d}y} \\&= -\frac{\log _2{(y)} + \log _2{(e)}}{y}\left. \right| _{a+1}^{\infty } \\&= \frac{\log _2{(e)} + \log _2{(a + 1)}}{a + 1}\,\cdot \\ \end{aligned}$$

when $b \ne 1$, the integration is found as follows

$$\begin{aligned} A&= \int \limits _{a}^{\infty } {\log _2{(1 + x)} \frac{b}{(x + b)^2} \,\mathrm{d}x} \\&= \int \limits _{a+1}^{\infty } {\log _2{(y)} \frac{b}{(y + b - 1)^2} \,\mathrm{d}y} \\&= \frac{b}{b - 1} \frac{y \log _2{(y)} - (y + b - 1)\log _2{(y + b - 1)}}{y + b - 1}\left. \right| _{a+1}^{\infty } \\&= \frac{b}{b - 1} \frac{(a+b) \log _2{(a+b)} - (a+1) \log _2{(a+1)}}{a+b}\,\cdot \end{aligned}$$

Appendix 3: Derivation of Equation (29)

For $b > 0, A = \int \nolimits _{0}^{\infty } {\mathrm{Q}{(\sqrt{2 x})}\, \frac{x^{N-1}}{(x+b)^{N+1}} \,\mathrm{d}x}$ can be expressed as

$$\begin{aligned} A&= \int \limits _{0}^{\infty } {\int \limits _{\sqrt{2 x}}^{\infty }{\frac{1}{\sqrt{2 \pi }} \exp {(-\frac{1}{2}y^2)}\,\frac{x^{N-1}}{(x+b)^{N+1}} \,\mathrm{d}y} \,\mathrm{d}x} \\&= \frac{1}{\sqrt{2 \pi }} \int \limits _{0}^{\infty }{\exp {(-\frac{1}{2}y^2)} \int \limits _{0}^{\frac{1}{2}y^2}{\frac{x^{N-1}}{(x+b)^{N+1}} \,\mathrm{d}x} \,\mathrm{d}y} \\&= \frac{1}{\sqrt{2 \pi }} \int \limits _{0}^{\infty }{\exp {(-\frac{1}{2}y^2)} \frac{1}{b N} \left( \frac{y^2/2}{y^2/2+b}\right) ^{N}\,\mathrm{d}y}\\&\stackrel{(i)}{=} \frac{1}{2 b N} \frac{1}{\sqrt{\pi }} \int \limits _{0}^{\infty }{e^{-t} \frac{t^{N-1/2}}{(t + b)^N}\,\mathrm{d}t} \\&= \frac{{{}_1\mathrm{F}_1}(N , \frac{1}{2}, b) - 2 \sqrt{b}\, \frac{\Gamma (N + \frac{1}{2})}{\Gamma (N)} \, {{}_1\mathrm{F}_1}(N + \frac{1}{2}, \frac{3}{2}, b)}{2 b N} , \end{aligned}$$

where $(i)$ is found by using $t = \frac{1}{2}y^2, \Gamma (\cdot )$ is the Gamma function, and ${{}_1\mathrm{F}_1}(\cdot , \cdot , \cdot )$ is the Kummer confluent Hypergeometric function.