Performance of a Multi-hop UWB Transmitted Reference System using Decode-and-Forward Relays

Abstract

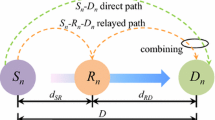
In this paper, end-to-end average bit error rate (ABER) of a multi-hop decode-and-forward relay system is evaluated using ultra-wideband transmitted reference (TR) receiver over a multi-path fading channel. Distribution of individual hop signal to noise ratio (SNR) is approximated by a log-normal distribution and corresponding ABER is evaluated by Gauss-Hermite Quadrature rule. These individual hop ABERs are then used to find the end-to-end ABER performance analytically which is faster than the simulation method available in the literatures. Performances of three variants of non-coherent TR receivers: simple transmitted reference, average transmitted reference and differential transmitted reference (DTR) receivers are compared assuming same total transmit power for a fixed end-to-end distance in line-of-sight (LOS) and non line-of-sight (NLOS) channel model. It is observed that the end-to-end ABER performance using DTR receivers is the best and multi-hop relaying is also most effective using these receivers to improve the performance. It is also found that the laws of diminishing returns hold for performance gain in average transmit SNR per bit at a particular ABER in LOS channel i.e. performance improvement in terms of transmit SNR is not equal as the number of hop increases. It decreases with increase in hop number but the reverse trend can be found in NLOS channel.

Evaluation of \(\mu _\gamma \) and \(\sigma _\gamma \)

To evaluate the $\mu _\gamma$ and $\sigma _\gamma$ we need to first calculate the $\mu _\alpha$ and $\sigma _\alpha ^2$ the mean and variance of $\ln \alpha$. Applying Wilkinson’s method to (13) which matches the first two moments of the sum of log-normals with that of approximated log-normal, the $\mu _\alpha$ and $\sigma _\alpha ^2$ can be found following [16].

$$\begin{aligned} \mu _\alpha&= 2 \ln u_1 -\frac{1}{2} \ln u_2 \nonumber \\ \sigma _\alpha ^2&= \ln u_2 -2 \ln u_1 \end{aligned}$$

(20)

where with $L$ number of resolvable multi-paths $u_1$ and $u_2$ can be expressed as

$$\begin{aligned} u_1&= \sum _{k=0}^{L-1} e^{2\lambda \mu _{\beta _k}+2{(\lambda \sigma _{\beta _k})}^2} \end{aligned}$$

(21)

$$\begin{aligned} u_2&= \sum _{k=0}^{L-1} e^{4\lambda \mu _{\beta _k}+8{(\lambda \sigma _{\beta _k})}^2} + 2 \sum _{k=0}^{L-2} \sum _{l=k+1}^{L-1} e^{2\lambda \mu _{\beta _k}+2\lambda \mu _{\beta _l} + 2{(\lambda \sigma _{\beta _k})}^2 +2{(\lambda \sigma _{\beta _l})}^2} \end{aligned}$$

(22)

Using the fact that the constant multiplied to a log-normal only shifts its mean of the associated Gaussian and keeps variance unchanged, the mean $\mu _{num}$ and variance $\sigma _{num}^2$ of the Gaussian $\ln (K_1 \alpha ^2)$ associated to the numerator of (12) is

$$\begin{aligned} \mu _{num}&= \ln K_1 + 2\mu _{\alpha } \nonumber \\ \sigma _{num}^2&= 4\sigma _\alpha ^2 \end{aligned}$$

(23)

The mean $\mu _{deno}$ and variance $\sigma _{deno}^2$ of the Gaussian $\ln (K_1 \alpha ^2 +1)$ associated to the denominator of (12) can be evaluated using Wilkinson’s method following the same approach as in (20) with $L=2$. The mean and variances of the two log-normals whose sum is of concern, take values as discussed in the Sect. 5.2. Then finally $\mu _\gamma$ and $\sigma _\gamma$ can be evaluated as using the properties (ii) and (i) of Sect. 5.2 subsequently.

$$\begin{aligned} \mu _\gamma&= \mu _{num} -\mu _{deno} \nonumber \\ \sigma _\gamma ^2&= \sigma _{num}^2 + \sigma _{deno}^2 \end{aligned}$$

(24)

The results obtained in (24) can then be used in (17) to get the individual hop ABER $P_{bit}$ and subsequently end-to-end ABER in (18).