Novel Algorithms for Quadratic Programming by Using Hypergraph Representations

Abstract

In this paper novel algorithms are introduced for solving NP hard discrete quadratic optimization problems commonly referred to as unconstrained binary quadratic programming. The proposed methods are based on hypergraph representation and recursive reduction of the dimension of the search space. In this way, efficient and fast search can be carried out and high quality suboptimal solutions can be obtained in real-time. The new algorithms can directly be applied to the quadratic problems of present day communication technologies, such as multiuser detection and scheduling providing fast optimization and increasing the performance. In the case of multiuser detection, the achieved bit error rate can approximate the Bayesian optimum and in the case of scheduling better Weighted Tardiness can be achieved by running the proposed algorithms. The methods are also tested on large scale quadratic problems selected from ORLIB and the solutions are compared to the ones obtained by traditional algorithms, such as Devour digest tidy-up, Hopfield neural network, local search, Taboo search and semi definite relaxing. As the corresponding performance analysis reveals the proposed methods can perform better than the traditional ones with similar complexity.

Appendix

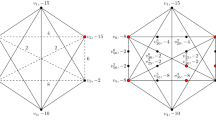
1.1 Description of the Algorithms

In this appendix we give the precise definition of the algorithms used in this article. We define the rules presented in Sect. 4.

1.1.1 Dimension Reduction of the Greedy Algorithm: L01

This algorithm uses a greedy strategy at the hypergraph level to determine in which direction the next hypernode falls. The algorithm stores the best N dimension candidate solution in $\mathbf {y^{opt}}$.

• 1. The algorithm starts at the original N dimension hypernode.

• 2. The inner solver is chosen to be a DHNN structure.

• 3. The performance of a “candidate solution” is defined by the value of the N dimension quadratic function on this solution.

• 4. We use the “inner solver” in every hypernode.

• 5. The next $n-1$ dimension hypernode is chosen from an $n\le \hbox {N}$ dimension hypernode as follows ($\Psi$): We search all the possible $n-1$ dimension hypernodes accessible from the current hypernode, and pick the best among them, which is performed by the following steps:

  • We assume that if we are in an arbitrary $n\le \hbox {N}$ dimension hypernode the best N dimension candidate solutions is accessible in $\mathbf {y}^{opt}$.

  • We select a starting point in an $n-1$ dimension hypernode for the “inner solver” from the actual $\mathbf {y}^{opt}$ by discarding the appropriate dimensions.

  • In each $n-1$ dimension hypernode the “inner solver” generates a $n-1$ dimension candidate solution, we denote it with $\mathbf {y^*}^{(i)}(\hbox {next})$.

  • We map every $\mathbf {y^*}^{(i)}(\hbox {next})$ back to the original N dimension space by filling the missing coordinates of $\mathbf {y^\dagger }^{(i)}(\hbox {next})$ with the coordinates of $\mathbf {y}^{opt}$.

  • According to the N dimension quadratic function we pick the best $\mathbf {y^\dagger }^{(i)}(\hbox {next})$ and compare with the value of the quadratic function taken over $\mathbf {y}^{opt}$.

  • If the performance is improved we choose that hypernode.

• 6. If not, the algorithm stops.

1.1.2 Dimension Reduction of the First Chance Algorithm: D01

This algorithm is different from the one described above in one rule. We do not evaluate all possible lower dimension hypernodes, but if we find one which gives a better candidate solution then we choose that hypernode. So instead of a full evaluation we introduce a “first-improve” strategy.

• 1. The algorithm starts at the original N dimension hypernode.

• 2. The inner solver is chosen to be a DHNN structure.

• 3. The performance of a “candidate solution” is defined by the value of the N dimension quadratic function on this solution.

• 4. We use the “inner solver” in every hypernode.

• 5. The next hypernode from an $n\le \hbox {N}$ dimension hypernode is chosen as follows $(\Psi )$. We pick one by one a possible $n-1$ dimension hypernode from the current node and if it improves our current candidate solution, we choose that hypernode, which is performed by the following steps:

  • We assume that if we are in an arbitrary $n\le \hbox {N}$ dimension hypernode the best N dimension candidate solutions is accessible in $\mathbf {y}^{opt}$.

  • We select a starting point in an $n-1$ dimension hypernode for the “inner solver” from the actual $\mathbf {y}^{opt}$ by discarding the appropriate dimensions.

  • In that $n-1$ dimension hypernode the “inner solver” generates one specific $n-1$ dimension candidate solution, we denote it by $\mathbf {y^*}^{(i)}(\hbox {next})$.

  • We map $\mathbf {y^*}^{(i)}(\hbox {next})$ back to the original N dimension space by filling the missing coordinates of $\mathbf {y^\dagger }^{(i)}(\hbox {next})$ with the coordinates of $\mathbf {y}^{opt}$.

  • According to the N dimension quadratic function we compare them with each other.

  • If the performance is improved we choose that hypernode.

  • If not, we try another not yet inspected hypernode in the $n-1$ dimension regime.

• 6. If we inspected every possible $n-1$ dimension hypernode and did not find a better candidate solution, the algorithm stops.

1.1.3 The Description of Dimension Adder DA01 Algorithm

This algorithm constructs a candidate solution gradually by adding dimensions starting from a low dimension hypernode until it reaches the highest dimension hypernode.

• 1. The algorithm starts from the 0 dimension hypernode.

• 2. The inner solver is chosen to be a DHNN structure.

• 3. The performance of a candidate solution depends on the dimension as we leave out the corresponding parts of the matrix and vector of the original N dimension quadratic function

• 4. We use the “inner solver” in every hypernode.

• 5. The next hypernode from an $n\le \hbox {N}$ dimension hypernode is chosen as follows $(\Psi )$: We pick one by one a possible $n+1$ dimension hypernode from the current node and if it improves our current candidate solution, we choose that hypernode, which is performed by the following steps:

  • We denote the set containing the indices of the coordinates of the current $n$ dimension hypernode with $C$. We denote the proposed candidate solution in this hypernode with $\mathbf {y}^*$.

  • We choose randomly a dimension which has not yet been picked, denoted by: $B =\{i\},i\ni C$.

  • We inspect the $n+1$ dimension hypernode with dimension indices $A = C \cup B$ with the “inner solver”.

  • At the inspected $n+1$ dimension hypernode the starting point of the “inner solver” (denoted by $\mathbf {y}$) is generated via copying the appropriate coordinates from the best found candidate solution and computing the missing coordinate via the gradient. $\mathbf {y}_ C =\mathbf {y}^*$ and $\mathbf {y}_\mathrm{B}=-{{\mathrm{sgn}}}(\mathbf {W^\mathrm{orig}}_\mathrm{B,C} \cdot \mathbf {y}^* - \mathbf {b^\mathrm{orig}}_\mathrm{B})$

  • We use the “inner solver” to get $\mathbf {y^*}\hbox {(next)}$ from $\mathbf {y}$.

• 6. If the Nth dimension was also added to the problem we stop and put $\mathbf {y}^{opt}=\mathbf {y^*}\hbox {(next)}$.

1.1.4 The Description of the Dimension Adder DA02 Algorithm

This algorithm is similar DA01 algorithm. It also constructs a candidate solution from a lower dimension one, but instead of a first-improve hypernode choice strategy this inspects all the possible one distance higher dimension hypernodes and chooses the best one.

• 1. The algorithm starts from the 0 dimension hypernode.

• 2. The “inner solver” is a DHNN structure.

• 3. The performance of a candidate solution here is dynamic. It is determined by the current $n=1\cdots \hbox {N}$ dimension quadratic function.

• 4. We use the “inner solver” in every hypernode.

• 5. The strategy by which we choose the next hypernode ($\Psi$) is the following:

  • We assume that if we are in an $n$ dimension hypernode, we also know the indices of the coordinates of the said hypernode. We denote this set with $C$, and the proposed candidate solution in this hypernode with $\mathbf {y}^*$.

  • We iterate through every dimension index which we did not inspect so far:$\forall i: B =\{i\},i\ni C$. We inspect all the possible $n+1$ dimension hypernode with dimension indices $A = C \cup B$ with the “inner solver”.

  • At each inspected $n+1$ dimension hypernode the starting point of the “inner solver” (denoted by $\mathbf {y}^{(i)}$) is generated via copying the appropriate coordinates from the best found candidate solution and computing the missing coordinate via the gradient. $\mathbf {y}^{(i)}_ C =\mathbf {y}^*$ and $\mathbf {y}^{(i)}_\mathrm{B}=-{{\mathrm{sgn}}}(\mathbf {W^\mathrm{orig}}_\mathrm{B,C} \cdot \mathbf {y}^* - \mathbf {b^\mathrm{orig}}_\mathrm{B})$

  • We use the “inner solver” to get $\mathbf {y^*}^{(i)}\hbox {(next)}$ from $\mathbf {y}^{(i)}$.

  • We choose the best performing $\mathbf {y^*}^{(i)}\hbox {(next)}$ and the corresponding hypernode for the next iteration.

• 6. If the Nth dimension was inspected as well the algorithm stops, and we put $\mathbf {y}^{opt}=\mathbf {y^*}\hbox {(next)}$.

1.2 Run-Time and Performance Analysis Tables

See Tables 3 and 4.

Table 3 Performance analysis table for the ORLIB problems

Table 4 Run time table for the ORLIB problems