Abstract
This paper studies differential space-time modulation using diversity-encoded differential amplitude and phase shift keying (DAPSK) for the multiple-input multiple-output (MIMO) system over independent but not identically distributed (inid) time-correlated Rician fading channels. An asymptotic maximum likelihood (AML) receiver is developed for differentially detecting diversity-encoded DAPSK symbol signals by operating on two consecutive received symbol blocks sequentially. Based on Beaulieu’s convergent series, the bit error probability (BEP) upper bound is analyzed for the AML receiver over inid time-correlated Rician fading channels. Particularly, an approximate BEP upper bound of the AML receiver is also derived for inid time-invariant Rayleigh fading channels with large received signal-to-noise power ratios. By virtue of this approximate bound, a design criterion is developed to determine the appropriate diversity encoding coefficients for the proposed DAPSK MIMO system. Numerical and simulation results show that the AML receiver for diversity-encoded DAPSK is nearly optimum when the average received signal-to-noise power ratios are high and the channel is heavily correlated fading and can provide better error performance than conventional noncoherent MIMO systems when the effect of non-ideal transmit power amplification is taken into account.








Similar content being viewed by others
Notes
Notably, all entries of the transmitted symbol matrix for DUSTM using APSK-based OSTCC take value in irregular symbol constellations. However, its PAPR value is fixed by 3 dB [16].
As indicated in [23], the error performance of DAPSK is highly sensitive to the amplitude ring ratio \(\mu \) in single-input multiple-output antenna systems, especially when the number of amplitude rings is large. This amplitude ring ratio parameter will be optimized in Sect. 4 through minimizing the BEP upper bound developed therein.
The rows of Walsh Hadamard and discrete Fourier transform matrices can be used as the dispersion vectors in the paper.
When \(\mathcal {S}\) is given, \(|x_{k}^{(i-1)}|\) and \( d_{k}=x_{k}^{(i)}/x_{k}^{(i-1)}\) that are required in the following analysis are, respectively given by \(|x_{k}^{(i-1)}|\, =\lambda \mu ^{(\beta _{k}^{(a)}a^{(i-1)}+a_{k}^{(0)})_{N}}\) and \(d_{k}=\mu ^{(\beta _{k}^{(a)}(a^{(i-1)}+\varDelta a)_{N}+a_{k}^{(0)})_{N}-(\beta _{k}^{(a)}a^{(i-1)}+a_{k}^{(0)})_{N}}\exp \{\frac{j2\pi \beta _{k}^{(p)}\varDelta b}{M}\}\) provided with predetermined \(\beta _{k}^{(a)},\, \beta _{k}^{(p)}\), and \(a_{k}^{(0)}\) for \(k\in \mathcal {Z}_{L_{t}}^{+}\).
As shown in (11), \(|d_{k}|\, =\mu ^{(\beta _{k}^{(a)}(a^{(i-1)}+\varDelta a)_{N}+a_{k}^{(0)})_{N}-(\beta _{k}^{(a)}a^{(i-1)}+a_{k}^{(0)})_{N}}\) takes the form \(\mu ^{0}\) when \( \varDelta a=0\). When \(\varDelta a\ne 0\), it takes the form \(\mu ^{(\beta _{k}^{(a)}\varDelta a)_{N}}\) if \(|d_{k}|\, >1\) and \(\mu ^{(\beta _{k}^{(a)}\varDelta a)_{N}-N}\) if \(|d_{k}|\, <1\).
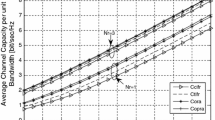
For conventional DNUSTM and DUSTM techniques, each data symbol is differentially encoded into two adjacently transmitted \(L_{t}\times L_{t}\) matrices and each transmitted matrix is emitted every \(L_{t}T_{s}\) seconds. Because \(L_{t}\) encoded symbols are transmitted at each antenna in each \( L_{t}T_{s}\) seconds, all the existing techniques operating at a rate of \(R\) bits per transmit antenna per \(L_{t}T_{s}\) provide a bandwidth efficiency of \(R\) bits\(/\)sec\(/\)channel use.
In the following, the initial transmitted symbol matrices used for all compared DNUSTM and DUSTM techniques are set to the identity matrix.
References
Tarokh, V., Seshadri, N., & Calderbank, A. R. (1998). Space-time codes for high data rate wireless communication: Performance criterion and code construction. IEEE Transactions on Information Theory, 44(2), 744–765.
Hochwald, B. M., & Marzetta, T. L. (2000). Unitary space-time modulation for multiple-antenna communications in Rayleigh flat fading. IEEE Transactions on Information Theory, 46(2), 543–564.
Hassibi, B., & Hochwald, B. M. (2002). High-rate codes that are linear in space and time. IEEE Transactions on Information Theory, 48(7), 1804–1824.
Yuen, C., Guan, Y. L., & Tjhung, T. T. (2008). Power-balanced orthogonal space-time block code. IEEE Transactions on Vehicular Technology, 57(5), 3304–3309.
Das, S., & Rajan, B. S. (2009). Square complex orthogonal designs with low PAPR and signaling complexity. IEEE Transactions on Wireless Communications, 8(1), 204–213.
Zheng, L., & Tse, D. N. C. (2003). Diversity and multiplexing: A fundamental tradeoff in multiple-antenna channels. IEEE Transactions on Information Theory, 49(5), 1073–1096.
Belfiore, J.-C., Rekaya, G., & Viterbo, E. (2005). The Golden code: A 2x2 full-rate space-time code with nonvanishing determinants. IEEE Transactions on Information Theory, 51(4), 1432–1436.
Sethuraman, B. A., Rajan, B. S., & Shashidhar, V. (2003). Full-diversity, high-rate space-time block codes from division algebras. IEEE Transactions on Information Theory, 49(10), 2596–2616.
Hochwald, B. M., & Sweldens, W. (2000). Differential unitary space-time modulation. IEEE Transactions on Communications, 48(12), 2041–2052.
Brehler, M., & Varanasi, M. K. (2001). Asymptotic error probability analysis of quadratic receivers in Rayleigh-fading channels with applications to a unified analysis of coherent and noncoherent space-time receivers. IEEE Transactions on Information Theory, 47(6), 2383–2399.
Hughes, B. L. (2000). Differential space-time modulation. IEEE Transactions on Information Theory, 46(7), 2567–2578.
Schober, R., & Lampe, L. H. J. (2002). Differential modulation diversity. IEEE Transactions on Vehicular Technology, 51(6), 1431–1444.
Tao, M. (2009). Effects of non-identical Rayleigh fading on differential unitary space-time modulation. IEEE Transactions on Communications, 57(5), 1359–1369.
Tarokh, V., & Jafarkhani, H. (2000). A differential detection scheme for transmit diversity. IEEE Journal on Selected Areas in Communications, 18(7), 1169–1174.
Ganesan, G., & Stoica, P. (2002). Differential modulation using space-time block codes. IEEE Signal Processing Letters, 9(2), 57–60.
Song, A., Wang, G., Su, W., & Xia, X.-G. (2004). Unitary space-time codes from Alamouti’s scheme with APSK signals. IEEE Transactions on Wireless Communications, 3(6), 2374–2384.
Bhatnagar, M. R., Hjørungnes, A., & Song, L. (2009). Differential coding for non-orthogonal space-time block codes with non-unitary constellations over arbitrarily correlated Rayleigh channels. IEEE Transactions on Wireless Communications, 8(8), 3985–3995.
Yu, X., Xu, D., & Bi, G. (2006). Differential space-time coding scheme using star quadrature amplitude modulation method. EURASIP Journal on Advances in Signal Processing, 2006(2006), 1–12.
Bauch, G. (2008). Bandwidth-efficient differential space-time modulation. IEEE Transactions on Vehicular Technology, 57(5), 2792–2803.
Ryu, H.-G., Park, J. S., & Park, J.-S. (2004). Threshold IBO of HPA in the predistorted OFDM communication system. IEEE Transactions on Broadcasting, 50(4), 425–428.
Costa, E., & Pupolin, S. (2002). M-QAM-OFDM system performance in the presence of a nonlinear amplifier and phase noise. IEEE Transactions on Communications, 50(3), 462–472.
Beaulieu, N. C. (1990). An infinite series for the computation of the complementary probability distribution function of a sum of independent random variables and its application to the sum of Rayleigh random variables. IEEE Transactions on Communications, 38(9), 1463–1474.
Chung, C.-D. (1997). Differentially amplitude and phase-encoded QAM for the correlated Rayleigh-fading channel with diversity reception. IEEE Transactions on Communications, 45(3), 309–321.
Huang, C.-H., & Chung, C.-D. (2012). Differentially amplitude- and phase-encoded QAM for amplify-and-forward multiple-relay systems. IEEE Transactions on Vehicular Technology, 61(5), 2054–2066.
Ma, Y., Zhang, Q. T., Schober, R., & Pasupathy, S. (2005). Diversity reception of DAPSK over generalized fading channels. IEEE Transactions on Wireless Communications, 4(4), 1834–1846.
Tjhung, T. T., Dong, X., Adachi, F., & Tan, K. H. (1997). On diversity reception of narrowband 16 star-QAM in fast Rician fading. IEEE Transactions on Vehicular Technology, 46(4), 923–932.
Proakis, J. G., & Salehi, M. (2008). Digital communications (5th ed.). New York: McGraw-Hill.
Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series, and products (6th ed.). San Diego, CA: Academic Press.
Larson, H. J., & Shubert, B. O. (1979). Probabilistic models in engineering sciences. New York: Wiley.
Rappaport, T. S. (1996). Wireless communications: Principles and practice. Englewood Cliffs, NJ: Prentice Hall.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Derivation of (18)
Given \(\mathcal {S}\) and \(\mathcal {S}_{d},\, Q_{kl}\) in (17) is a conditionally GQS of \(U_{kl}\) and \(V_{kl}\) which have means \(\overline{U} _{kl}\triangleq \mathbb {E}\{U_{kl}|\mathcal {S},\mathcal {S}_{d}\}=\sqrt{ \gamma _{kl}/\varGamma _{kl}}\tau _{kl}(d_{k}-\widehat{d}_{k})x_{k}^{(i-1)}\) and \(\overline{V}_{kl}\triangleq \mathbb {E}\left\{ V_{kl}|\mathcal {S}, \mathcal {S}_{d}\right\} =0\) and second central moments
With reference to [27, eq. (B-5)], the conditional MGF \(\varPhi _{Q_{kl}}(s|\mathcal {S},\mathcal {S}_{d})\) is given by (18) with
Note that \(v_{kl}^{(1)}v_{kl}^{(2)}=-u_{kl}\). Using (25)–(27 ), \(\phi _{kl}^{(1)}\phi _{kl}^{(2)}-|\phi _{kl}^{(3)}|^{2}\) can be further expressed as
For \(d_{k}\ne \widehat{d}_{k},\, \phi _{kl}^{(1)}\phi _{kl}^{(2)}-|\phi _{kl}^{(3)}|^{2}\) is always positive, and then \(v_{kl}^{(1)}>0\) and \( v_{kl}^{(2)}<0\) from (28).
1.2 Derivations of (23) and (24)
When \(\varOmega _{kl}=0\) and \(\rho _{kl}=1\) for all \(k\in \mathcal {Z} _{L_{t}}^{+}\) and \(l\in \mathcal {Z}_{L_{r}}^{+}\), the conditional MGF \(\varPhi _{Q}(s|\mathcal {S},\mathcal {S}_{d})\) in (18) specializes to
where \(v_{kl}\) and \(u_{kl}\) in (29) simplify, respectively to
When \(\gamma _{t}\gg 1,\, v_{kl}\) and \(u_{kl}\) can be further approximated as \(v_{kl}\approx 1/2\) and \(u_{kl}\approx (1+|\widehat{d}_{k}|^{2})/(|d_{k}- \widehat{d}_{k}|^{2}|x_{k}^{(i-1)}|^{2}g_{k}\varGamma _{kl}\gamma _{t})\), and thus \(v_{kl}^{(1)}\) and \(v_{kl}^{(2)}\) in (28) are approximated as \( v_{kl}^{(1)}\approx 0\) and \(v_{kl}^{(2)}\approx -1\) for \(k\in \mathcal {Z} _{L_{t}}^{+}\) and \(l\in \mathcal {Z}_{L_{r}}^{+}\) because \(u_{kl}\) is much smaller than \(v_{kl}\) for large \(\gamma _{t}\) values. Using this approximation, \(\varPhi _{Q}\left( s|\mathcal {S},\mathcal {S}_{d}\right) \) in ( 31) can be approximated for \(\gamma _{t}\gg 1\) as
Putting the high SNR approximation of \(\Pr \{Q<\vartheta |\mathcal {S}, \mathcal {S}_{d}\}\) in (32) into (21) yields
Using Leibniz’s rule of differentiation in [28, eq. (0.42)], we have
Rights and permissions
About this article
Cite this article
Huang, CH., Chung, CD. Differential Space-Time Modulation Using DAPSK Over Rician Fading Channels. Wireless Pers Commun 78, 1021–1046 (2014). https://doi.org/10.1007/s11277-014-1799-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-014-1799-7