Skip to main content

Advertisement

Springer Nature Link
Log in

Lattice Sphere Decoding for Data Transmission Systems with Special Channel Matrices

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

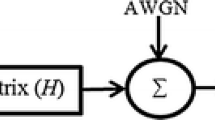
This paper presents the effects of condition number (\(\tau \)) in communication system performance. It has been shown that a small condition number (\(\tau \)) results a better performance. The proposed scheme is using special kind of matrices with Lattice Sphere Decoding (LSD) technique for Block Data Transmission Systems (BDTS). Hankel and Toeplitz matrices are used separately as a channel matrix (H) while circulant matrix is used in the previous works. The proposed scheme reduced the condition number (\(\tau \)) and, therefore, improve the system performance. As a result; LSD-based BDTS with Toeplitz/Hankel matrix outperforms the LSD-based BDTS with circulant matrix. Complexity analysis is also done which based on lattice dimension and initial radius selection.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Babu, S. P. K., Salleh, M. F. M., & Ghani, F. (2009). Reduced complexity optimum detector for block data transmission systems. IEICE Electronics Express (ELEX), 6(23), 1649–1655.

    Article  Google Scholar 

  2. Li, X., & Cui, X. (2004). Application of lattice code decoder to SC-CP for short block length. Electronics Letters, 40(15), 954–955.

    Article  Google Scholar 

  3. Albreem, M. A. M., Salleh, M. F. M., & Babu, S. P. K. (2011). Reduced complexity optimum detector for block data transmission systems using lattice sphere decoding technique. IEICE Electronics Express (ELEX), 8(9), 644–649.

    Article  Google Scholar 

  4. Barbero, L. G., & Thompson, J. S. (2008). Fixing the complexity of the sphere decoder for MIMO detection. IEEE Transactions on Wireless Communications, 7(6), 2131–2143.

    Article  Google Scholar 

  5. Kreyszig, E. (2011). Advanced engineering mathematircs (10th ed., pp. 861–867). New York: Wiley.

    Google Scholar 

  6. Conway, J. H., & Sloane, N. J. A. (1999). Sphere packings, lattices and goups. Berlin: Springer.

    Book  Google Scholar 

  7. Roger, S., Gonzalez, A., Almenar, V., & Vidal, A. (2009). MIMO channel matrix condition number estimation and threshold selection for combined K-best sphere decoders. IEICE Transactions on Communications, E92–B(4), 1380–1383.

    Article  Google Scholar 

  8. Higham, D. J. (1995). Condition numbers and their condition numbers. Linear Algebra and its Application, 214, 193–213.

    Article  MathSciNet  MATH  Google Scholar 

  9. Cui, T., & Tellambura, C. (2005). An efficient generalized sphere decoder for rank-deficient MIMO systems. IEEE Communication Letters, 9(5), 423–425.

    Article  Google Scholar 

  10. Hassibi, B., & Vikalo, H. (2005). On the sphere-decoding algorithm I. Expected complexity. IEEE Transactions on Signal Processing, 53(8), 2806–2818.

    Article  MathSciNet  Google Scholar 

  11. Dianat, S. A., & Saber, E. S. (2009). Advanced Linear Algebra for Engineers with MATLAB (1st ed.). Bacoraton, FL: CRC Press.

    Book  MATH  Google Scholar 

  12. Ramamurthy, G. (July 2009). Left circulant and generator type matrices, Report No: IIIT/TR/2009/155. Theory and Algorithms International Institute of Information Technology, India: Centre for Security.

  13. Albreem, M. A. M., & Salleh, M. F. M. (2013). Near-\(A_n\)-lattice sphere decoding technique assisted optimum detection for block data transmission systems. IEICE Transactions on Communications, E96–B(1), 356–359.

    Article  Google Scholar 

  14. Yang, L., Chen, R. S., Soo, K. K., & Siu, Y. M. (2007). An efficient sphere decoding approach for PTS assisted PAPR reduction of OFDM signals. International Journal of Electronics and Communications (AEÜ), 61, 684–688.

    Article  Google Scholar 

  15. Tse, D., & Viswanath, P. (2005). Fundamental of wireless communication. Cambridge: Cambridge University Press.

    Book  Google Scholar 

  16. Lee, E. A. (1994). Digital communication. London: Kluwer Academic.

    Book  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the Universiti Sains Malaysia (USM) for the financial supports and fellowship.

Author information

Authors and Affiliations

  1. School of Electrical System Engineering, University Malaysia Perlis (UniMAP), Kangar, Malaysia

    Mahmoud A. M. Albreem

  2. School of Electrical and Electronic Engineering, Universiti Sains Malaysia (USM), Penang, Malaysia

    Mohd Fadzli Mohd Salleh

Authors
  1. Mahmoud A. M. Albreem
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mohd Fadzli Mohd Salleh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mahmoud A. M. Albreem.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Albreem, M.A.M., Salleh, M.F.M. Lattice Sphere Decoding for Data Transmission Systems with Special Channel Matrices. Wireless Pers Commun 79, 265–277 (2014). https://doi.org/10.1007/s11277-014-1855-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-014-1855-3

Keywords