Abstract
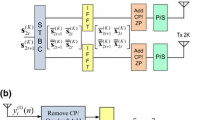
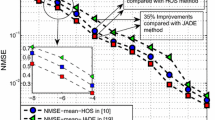
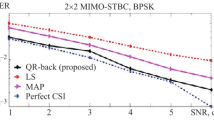
In this paper, we concern the channel estimation for a wireless communication system in which the techniques of multiple-input multiple-output, code division multiple access (CDMA) and orthogonal space-time block codes (OSTBCs) are integrated together for the purpose of achieving high data rate. We show that a composite channel information (CCI) vector can be formed, which contains the effects of channel state information, spreading coding and OSTBCs. From the standpoint of the MUltiple SIgnal Classification method, such CCI vector must lie in the signal subspace spanned by the dominant eigenvectors of the received data covariance matrix. Also, this CCI vector is located in another subspace which is associated with the CDMA and OSTBC codes and can be computed off-line. Using the vector space projections method, this CCI vector can be viewed as the intersection of these two subspaces and thus can be computed by alternative projections. In order to reduce the computation complexity, we propose an equivalent but computationally effective single-step solution in which the channel estimation amounts to searching for the principal eigenvector of a certain matrix with moderate size. Additionally, only one training block is required to overcome the problem of sign ambiguity. Numerical results demonstrate that, in addition to improving the bandwidth efficiency, the proposed method offers better performance in terms of channel estimation accuracy and bit-error-rate as compared with the standard nonblind least-squares channel estimation approach.








Similar content being viewed by others
References
Pan, P., Zhang, Y., Sun, Y., & Yang, L.-L. (2013). On the asymptotic spectral efficiency of uplink MIMO-CDMA systems over Rayleigh fading channels with arbitrary spatial correlation. IEEE Transactions on Vehicular Technology, 62(2), 679–691.
Tu, Y.-P., Lu, H.-Y., & Fang, W.-H. (2012). Alternating multiuser detection with soft interference cancellation for heterogeneous-signaling MIMO CDMA systems. Wireless Personal Communication. doi:10.1007/s11277-011-0412-6.
Liao, D., Qiu, D., & Elhakeem, A. K. (2010). Performance analysis of MIMO based CDMA code acquisition over Rayleigh fading channels. Wireless Personal Communication. doi:10.1007/s11277-009-9809-x.
Takeuchi, K., Vehkapera, M., Tanaka, T., & Muller, R. (2012). Large-system analysis of joint channel and data estimation for MIMO DS-CDMA systems. IEEE Transactions on Information Theory, 58(3), 1385–1412.
Assra, A., Hamouda, W., & Youssef, A. (2010). A channel-estimation and data-detection scheme for multiuser MIMO-CDMA systems in fading channels. IEEE Transactions on Vehicular Technology, 59(6), 2830–2844.
Driouch, E., & Ajib, W. (2012). Efficient scheduling algorithms for multiantenna CDMA systems. IEEE Transactions on Vehicular Technology, 61(2), 521–532.
Serbetli, S., & Yener, A. (2006). MIMO-CDMA systems: Signature and beamformer design with various levels of feedback. IEEE Transactions on Signal Processing, 54(7), 2758–2772.
Shahbazpanahi, S., Gershman, A. B., & Giannakis, G. B. (2006). Semiblind multiuser MIMO channel estimation using capon and MUSIC techniques. IEEE Transactions on Signal Processing, 54(9), 3581–3591.
Ding, Z., Ward, D. B., & Nabar, R. U. (2007). Joint channel estimation and symbol detection for orthogonal space-time block-coding systems in frequency-selective channels. IEEE Transactions on Vehicular Technology, 56(5), 2475–2486.
Rong, Y., Shahbazpanahi, S., & Gershman, A. B. (2005). Robust linear receivers for space-time block coded multiaccess MIMO systems with imperfect channel state information. IEEE Transactions on Signal Processing, 53(8), 3081–3090.
Cavalcante, R. L. G., & Yamada, I. (2008). Multiaccess interference suppression in orthogonal space-time block coded MIMO systems by adaptive projected subgradient method. IEEE Transactions on Signal Processing, 56(3), 1028–1042.
Sarmadi, N., Shahbazpanahi, S., & Gershman, A. B. (2009). Blind channel estimation in orthogonally coded MIMO-OFDM systems: A semidefinite relaxation approach. IEEE Transactions on Signal Processing, 57(6), 2354–2364.
Shahbazpanahi, S., Gershman, A. B., & Manton, J. H. (2005). Closed-form blind MIMO channel estimation for orthogonal space-time block codes. IEEE Transactions on Signal Processing, 53(12), 4506–4517.
Li, H., Lu, X., & Giannakis, G. B. (2002). Capon multiuser receiver for CDMA systems with space-time coding. IEEE Transactions on Signal Processing, 50(5), 1193–1204.
D’Orazio, L., Sacchi, C., Fedrizzi, R. & De Natale, F. G. B. (2007, November). An adaptive minimum-BER approach for multi-user detection in STBC-MIMO MC-CDMA systems. In IEEE global telecommunications conference 2007 (pp. 3427–3431).
De Lamare, R. C., & Sampaio-Neto, R. (2010). Blind adaptive MIMO receivers for space-time block-coded DS-CDMA systems in multipath channels using the constant modulus criterion. IEEE Transactions on Communications, 58(1), 21–27.
Beres, E., & Adve, R. (2007). Blind channel estimation for orthogonal STBC in MISO systems. IEEE Transactions on Vehicular Technology, 56(4), 2042–2050.
Sadler, D. J., & Manikas, A. (2003). Blind reception of multicarrier DS-CDMA using antenna arrays. IEEE Transactions on Wireless Communications, 2(6), 1231–1239.
Stark, H., & Yang, Y. (1998). Vector space projections: A numerical approach to signal and image processing, neural nets, and optics. New York, NY, USA: Wiley.
Zhuang, J., & Manikas, A. (2013). Interference cancellation beamforming robust to pointing errors. IET Signal Processing, 7(2), 120–127.
Zhang, F. (2011). Matrix theory: Basic results and techniques. Berlin: Springer.
Via, J., & Santamaria, I. (2008). Correlation matching approaches for blind OSTBC channel estimation. IEEE Transactions on Signal Processing, 56(12), 5950–5961.
Tarokh, V., Jafarkhani, H., & Calderbank, A. R. (1999). Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory, 45(5), 1456–1467.
Acknowledgments
This work was supported in part by the open research fund of Chongqing Key Laboratory of Emergency Communications under Grant No. CQKLEC20130504, the Scientific Research Foundation for the Returned Overseas Chinese Scholars (SRF for ROCS, SEM) under Grant No. LXHG-47-ZJ, the National Natural Science Foundation of China under Grant No. 61301272, the Program for Innovative Research Team in University of Chongqing under Grant No. KJTD201343, the Key Project of Chongqing Natural Science Foundation under Grant No. CSTC2011BA2016, the Program for New Century Excellent Talents in University under Grant No. NCET-11-0873 and the Program for Fundamental and Advanced Research of Chongqing under Grant No. CSTC2013JCYJA40045.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proof of (24)
In this “Appendix”, we prove (24). First, we can rewrite the matrix \({\varvec{\Upsilon }}_p\) as
where \(\mathbf {C}_p\) and \({\varvec{\Phi }}\) are defined in (1) and (12) respectively. Consequently, the matrix inner product \({\varvec{\Upsilon }}_p^T{\varvec{\Upsilon }}_p\) can be expressed as
where the properties \(\mathbf {c}_p^T\mathbf {c}_p=L_c\) and \({\varvec{\Phi }}_{k}^T{\varvec{\Phi }}_{k}=\mathbf {I}_{N_{T}N_r}\) are used in the above. Now the projector matrix \(\mathbf {P}_{cp}\) can be represented as follows
Appendix 2: Training-Based Least-Squares Channel Estimation
Following the work of [8], we can formulate the training-based least-squares (LS) channel estimator readily. First we can rewrite (13) as
where \(\widetilde{\mathbf {A}}(\underline{\mathbf {s}_p})\) is a \(2N_rT \times 2N_rN_t\) matrix whose \(k\)th column is given by
where \(\mathbf {e}_k\), as before, is the \(2N_rN_t\) vector having one in its \(k\)th position and zeros elsewhere. Then each user is assumed to transmits \(J_t\) training blocks, and thus we have
where \(\mathbf {s}_p(n)\) represents the \(n\)th known training symbol transmitted by the \(p\)th user, and \(\mathbf {Y}(n)\) and \(\mathbf {V}(n)\) are, respectively, the received signal matrix and the noise matrix for the \(n\)th training blocks. By defining
we can rewrite (41) as
Stacking the vectors \(\mathbf {y}(n) (n=1,\ldots ,J_t)\) in a longer \(2TN_rL_cJ_t \times 1\) vector
and defining the \(2TN_rL_cJ_t \times 2N_tN_r\) matrix
and the \(2TN_rL_cJ_t \times 1\) vector
we can rewrite (43) in a more compact form as
Based on (47), the LS estimate of the vector \(\mathbf {g}\) can be expressed as
Rights and permissions
About this article
Cite this article
Zhuang, J., Zhang, T., Li, H. et al. Semiblind Channel Estimation for Multiuser MIMO-CDMA Systems with Orthogonal Space-Time Block Codes. Wireless Pers Commun 79, 703–720 (2014). https://doi.org/10.1007/s11277-014-1881-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-014-1881-1