Incidence Coloring-Assisted Frequency Assignment in Two-Hop OFDMA-based Cellular Networks

Abstract

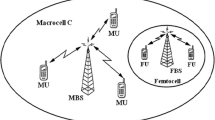
In this paper, we consider frequency assignment for orthogonal frequency division multiple access-based cellular networks. We develop a new framework for the mathematical modeling of the frequency assignment problem, which aims at suppressing multi-links interference and enhancing spectral efficiency. The concept of incidence coloring from modern graph theory is utilized to recast the original frequency assignment problem and guide the solution from graph theory perspective. In addition, optimal position of relay stations in a hierarchical cluster based two-hop cellular networks is investigated, and proposes an efficient frequency assignment scheme based on the incidence coloring. System-level simulation results demonstrate that the frequency assignment scheme can effectively mitigate inter-cell interference and improve signal-to-interference-plus-noise ratio. Compared with existing frequency assignment schemes, better coverage performance is obtained and throughput of cell-edge mobile stations is greatly improved.

Appendix: Mathematical Analysis and Theoretical Proof

In the new architecture, the cellular networks have been divided into regular triangles lattice, which is considered to be a graph whose nodes are the points of the lattice, and edges exist precisely between neighboring points.

Lemma 1

[29] Let $G$ be a graph with maximum degree$\Delta (G)$. Then, $\chi _i (G)\ge \Delta (G)+1$.

For a vertex $v$ of degree $\Delta (G)$, we must use $\Delta (G)$ colors for coloring $I_v$ and at least one additional color for coloring $A_v$.

Theorem 1

Let $G$ be a triangular lattice. Then, $\chi _i (G)=7$.

Proof

By Lemma 1, we know that $\chi _i (G)\ge \Delta (G)+1=7$. Thus, we only need to give a 7-incidence coloring $\sigma$ of $G$. Let $G$ be a triangular lattice as shown in Fig. 12 and we fix a vertex to be the original point $O(0,0)$ and impose a $XOY$ lattice coordinates to identify the vertices. Let the center vertex $O(0,0)$ in a triangular lattice be the origin and vertex $v$ be any other vertex in a triangular lattice with coordinates $(x,y)$, the coordinates of the six incidences of vertex $v$ in a triangular lattice are $(x,y+1),(x+1,y),(x+1,y-1),(x,y-1),(x-1,y)$ and $(x-1,y+1)$, respectively, as shown in Fig. 12. We then define $\phi (x,y)\equiv (3x+y)\mathrm{mod} 7$, where $(x,y)$ are the coordinates of any vertex. Let $\sigma$ be a $(\Delta +1)$-incidence coloring with color set $C=\left\{ {1,2,\ldots ,\Delta +1} \right\}$, and we divided the color set $C$ into seven subsets $C_0 ,C_1 ,\ldots ,C_6$, each subset includes $\Delta =6$ colors as follows: $C_0 =\{1,2,3,4,5,6\},C_1 =\{3,5,2,7,6,4\},C_2 =\{2,6,5,1,4,7\},C_3 =\{5,4,6,3,7,1\},C_4 =\{6,7,4,2,1,3\}$, $C_5 =\{4,1,7,5,3,2\}$, $C_6 =\{7,3,1,6,2,5\}$. $\square$

Fig. 12

Coordinates

Let $\sigma :I\rightarrow C$ and

$$\begin{aligned} I_{v_{(x,y)} } =\left\{ {\begin{array}{l} (v_{(x,y)} ,v_{(x,y)} v_{(x,y+1)} ),(v_{(x,y)} ,v_{(x,y)} v_{(x+1,y)} ), \\ (v_{(x,y)} ,v_{(x,y)} v_{(x+1,y-1)} ),(v_{(x,y)} ,v_{(x,y)} v_{(x,y-1)} ), \\ (v_{(x,y)} ,v_{(x,y)} v_{(x-1,y)} ),(v_{(x,y)} ,v_{(x,y)} v_{(x-1,y+1)} ) \\ \end{array}} \right\} \end{aligned}$$

Then, the incidence colors with respect to vertex $v_{(x,y)}$ can be obtained by the following formula:

$\phi (x,y)=i\;(i=0,1,2,3,4,5,6)$ and $\sigma (I_{v_{(x,y)} } )=C_i \;.$ It is easy to see that the coloring above is a proper 7-incidence coloring of $G$.