Abstract
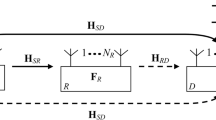
Our aim in this paper is to define a novel beamforming approach in wireless multiple-input-multiple-output (MIMO) code-division-multiple-access (CDMA) relay networks, which involves communication between multiple source-destination pairs. It is assumed that full channel state information of source-relay and relay-destination channels are available. Our design consists of a two-step amplify-and-forward protocol. The first step includes signal transmission from the sources to the MIMO relay, and the second step contains transmitting a version of the linear precoded signal to the destinations. Beamforming is investigated only in MIMO-relay node to reduce end user’s hardware complexity and save the computational power. Accordingly, the optimization problem is defined to find the MIMO relay beamforming coefficients that minimize total relay transmit power by keeping the signal-to-interference-plus-noise ratio (SINR) of all destinations above a certain threshold value. It is shown that such optimization problem is a non-convex quadratically constrained quadratic programming, which is NP-hard in general. However, by relaxing this problem to a semi-definite programming problem, the problem can be solved efficiently. Simulation results verify the performance gain implied by MIMO–CDMA relay system compared to the non-CDMA coded system.





Similar content being viewed by others
Notes
Semi Definite Representation.
Complex Symmetric Gaussian.
References
Laneman, J. N., Tse, D. N. C., & Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50, 3062–3080.
Golbon-Haghighi, M. H., Shirazi, M., Mahboobi, B., & Ardebilipour M. (2013). Optimal beamforming in wireless multiuser MIMO-relay networks. Presented at the 21st Iranian conference on electrical engineering (ICEE).
Laneman, J. N., & Wornell, G. W. (2003). Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory, 49, 2415–2425.
Kramer, G., Gastpar, M., & Gupta, P. (2005). Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory, 51, 3037–3063.
Todd, A. N., & Hunter, E. (2006). Diversity through coded cooperation. IEEE Transactions on Wireless Communication, 2, 283–289.
Nabar, R. U., Bolcskei, H., & Kneubuhler, F. W. (2004). Fading relay channels: Performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications, 22, 1099–1109.
Alikhani, E. S., Mahboobi, B., & Ardebilipour, M. (2012). Interference aware resource allocation in orthogonal frequency-division multiple access-based relay networks. Communications, IET, 6, 1364–1373.
Alikhani, E. S., Mahboobi, B., Ardebilipour, M., & Alikhani A. S. (2011). Resource allocation and frequency reusing for multihop relay systems. In 19th Iranian conference on electrical engineering (ICEE), pp. 1–6.
Alikhani, E. S., Mahboobi, B., Ardebilipour, M., Kheyri, H., & Alikhani, S. S. (2011). Adaptive radio resource allocation with frequency reusing for OFDMA cellular relay networks. In Third international conference on ubiquitous and future networks (ICUFN), pp. 395–400.
Mahboobi, B., & Ardebilipour, M. (2013). Joint power allocation and routing in full-duplex relay network: An outage probability approach.
Mahboobi, B., Mohammadi, M., Ardebilipour, M., & Moratab, A. (2010). In International congress on QoS aware power allocation in multi-hop multi-relay network., pp. 327–330.
Mohammadi, M., Mahboobi, B., Ardebilipour, M., & Mobini, Z. (2010). Power-optimized multi-hop multi-branch amplify-and-forward cooperative systems. In 5th IEEE international symposium on wireless pervasive computing (ISWPC), pp. 534–539.
Mohammadi, M., Mobini, Z., Ardebilipour, M., & Mahboobi, B. (2013). Performance analysis of generic amplify-and-forward cooperative networks over asymmetric fading channels. Wireless Personal Communications, 72, 49–70.
Raeisi, A., Mahboobi, B., Zokaei, S., & Ardebilipoor, M. (2010). Near-optimal joint routing and power allocation for amplify-and-forward multi-hop networks. In 18th conference on telecommunications forum (TELFOR).
Yindi, J., & Jafarkhani, H. (2009). Network beamforming using relays with perfect channel information. IEEE Transactions on Information Theory, 55, 2499–2517.
Havary-Nassab, V., Shahbazpanahi, S., Grami, A., & Zhi-Quan, L. (2008). Distributed beamforming for relay networks based on second-order statistics of the channel state information. IEEE Transactions on Signal Processing, 56, 4306–4316.
Fazeli-Dehkordy, S., Shahbazpanahi, S., & Gazor, S. (2009). Multiple peer-to-peer communications using a network of relays. IEEE Transactions on Signal Processing, 57, 3053–3062.
Chalise, B. K., & Vandendorpe, L. (2009). MIMO relay design for multipoint-to-multipoint communications with imperfect channel state information. IEEE Transactions on Signal Processing, 57, 2785–2796.
Chalise, B. K., & Vandendorpe, L. (2009). Joint optimization of multiple MIMO relays for multi-point to multi-point communication in wireless networks. In IEEE 10th workshop on signal processing advances in wireless communications, 2009. SPAWC ’09, pp. 479–483.
Golbon-Haghighi, M. H., Mahboobi, B., & Ardebilipour, M. (2013). Multiple antenna relay beamforming for wireless peer to peer communications. Journal of Information Systems and Telecommunication (JIST), 1, 209–215.
Sidiropoulos, N. D., Davidson, T. N., & Luo, Z.-Q. (2006). Transmit beamforming for physical-layer multicasting. IEEE Transactions on Signal Processing, 54, 2239–2251.
Boyd, A. D. A. A. S. (2003). Relaxations and randomized methods for nonconvex QCQPs. Stanford, CA: Stanford Universiy, Autumn 2003. www.standford.edu/class/ee392o,EE92o.
Peng, J., Roos, C., & Terlaky, T. (2002). Self-regularity: A new paradigm for primal-dual interior-point algorithms. Princeton: Princeton University Press.
Behbahani, A. S., Merched, R., & Eltawil, A. M. (2008). Optimizations of a MIMO relay network. IEEE Transactions on Signal Processing, 56, 5062–5073.
Tang, X., & Hua, Y. (2007). Optimal design of non-regenerative MIMO wireless relays. IEEE Transactions on Wireless Communications, 6, 1398–1407.
Poor, H. V., & Verdu, S. (1997). Probability of error in MMSE multiuser detection. IEEE Transactions on Informations Theory, 43, 858–871.
Verdu, S. (1998). MultiUser detection. Cambridge: Cambridge university press.
Guoping, Z., & Chin, F. (2004). Multi-antenna WCDMA receiver design with CORDIC. In 15th IEEE international symposium on personal, indoor and mobile radio communicagtions PIMRC, Vol. 4, pp. 2811–2814.
Wan, C., Andrews, J. G., & Heath, R. W. (2007). Multiuser antenna partitioning for cellular MIMO–CDMA systems. IEEE Transactions on Vehicular Technology, 56, 2448–2456.
Assra, A., Hamouda, W., & Youssef, A. (2010). EM-based joint channel estimation and data detection for MIMO–CDMA systems. IEEE Transactions on Vehicular Technology, 59, 1205–1216.
Tu, Y.-P., Lu, H.-Y., & Fang, W.-H. (2011) Alternating multiuser detection with soft interference cancellation for heterogeneous-signaling MIMO CDMA systems. Wireless personal communilcatgion, pp. 1–18.
Dempster, A., Laird, N., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society Series B (Methodological), 39, 1–38.
Driouch, E., & Ajib, W. (2012). Efficient scheduling algorithms for multiantenna CDMA systems. IEEE Transactions on Vehicular Technology, 61, 521–532.
Beheshti, S. M., Ardebilipour, M., & Mahboobi, B. (2011). Joint interference avoidance and spectrum sharing for unlicensed wireless systems. In 19th Iranian conference on electrical engineering (ICEE), pp. 1–6.
Havary-Nassab, V., Shahbazpanahi, S., & Grami, A. (2010). Optimal distributed beamforming for two-way relay networks. IEEE Transactions on Signal Processing, 58, 1238–1250.
Beheshti, S. M., Mahboobi, B., & Ardebilipour, M. (2011). Joint power adaptation and interference avoidance for unlicensed wireless systems: A game theoretic approach. International Journal of Information and Communication Technology, 3.
Popescu, D. C. & Rose, C. (2003). Interference avoidance for wireless systems. In Wiley encyclopedia of telecommunications. New York: Wiley.
Soleimani-Nasab, E., Ardebilipour, M., Kalantari, A., & Mahboobi, B. (2013). Performance analysis of multi-antenna relay networks with imperfect channel estimation. AEU-International Journal of Electronics and Communications, 67, 45–57.
Chalise, B. K., & Vandendorpe, L. Optimization of MIMO relays for multipoint-to-multipoint communications: Nonrobust and robust designs. IEEE Transactions on Signal Processing, 58, 6355–6368.
Mahboobi, B., Ardebilipour, M., Kalantari, A., & Soleimani-Nasab, E. (2013). Robust cooperative relay beamforming. IEEE Wireless Communications Letters, 2, 399–402.
Mahboobi, B., Soleimani-Nasab, E., & Ardebilipour, M. (2014). Outage probability based robust distributed beam-forming in multi-user cooperative networks with imperfect CSI. Wireless Personal Communications, 77, 1629–1658.
Horn, R. A., & Johnson, C. R. (1994). Topics in matrix analysis. Cambridge: Cambridge University Press.
Sturm, J. F. (1999). Using SeDuMi 1.02, a Matlab toolbox for optimization over symmetric cones. Optimization Methods and Software, 11–12, 625–653.
Grant, M., & Boyd, S. CVX: Matlab software for disciplined convex programming. http://stanford.edu/boyd/cvx.
Karipidis, E., Sidiropoulos, N. D., & Luo, Z.-Q. (2008). Quality of service and max–min fair transmit beamforming to multiple cochannel multicast groups. IEEE Transactions on Signal Processing, 56, 1268–1279.
Luo, Z.-Q., Sidiropoulos, N. D., Tseng, P., & Zhang, S. (2007). Approximation bounds for quadratic optimization with homogeneous quadratic constraints. SIAM Journal of Optimization, 18, 1–28.
Chang, T.-H., Luo, Z.-Q., & Chi, C.-Y. (2008). Approximation bounds for semidefinite relaxation of max–min-fair multicast transmit beamforming problem. IEEE Transactions on Signal Processing, 56, 3932–3943.
Ma, W.-K., Davidson, T. N., Wong, K. M., Luo, Z.-Q., & Ching, P.-C. (2002). Quasi-maximum-likelihood multiuser detection using semi-definite relaxation with application to synchronous CDMA. IEEE Transactions on Signal Processing, 50, 912–922.
Phan, A. H., Tuan, H. D., Kha, H. H., & Nguyen, H. H. (2012). Beamforming optimization in multiUser amplify-and-forward wireless relay networks. IEEE Transactions on Wireless Communication, 11, 1510–1520.
Tuy, H. (1998). Convex analysis and global optimization. London: Kluwer Academic.
Yongwei, H., & Palomar, D. P. (2010). Rank-constrained separable semidefinite programming with applications to optimal beamforming. IEEE Transactions on Signal Processing, 58, 664–678.
Rashid, U., Tuan, H. D. & Nguyen, H. H. (2012). Maximin relay beamforming in multiuser amplify-forward wireless relay networks. Presented at the wireless communication and networking conference (WCNC).
Tuan, H. D., Son, T. T., Tuy, H., & Nguyen, H. H. (2011). Optimum multi-user detection by nonsmooth optimization. Presented at the IEEE international conference on acoustics speech and signal process (ICASSP).
Nesterov, Y. E., & Nemirovskii, A. S. (1994). “Interior point polynomial algorithms in convex programming”, SIAM studies in applied mathematics (Vol. 13). Philadelphia, PA: SIAM.
Wolkowicz, H., Saigal, R., & Vandenberghe, L. (2000). Handbook of semidefinite programming theory, algorithms, and applications. New York: Springer.
Chalise, B. K., Vandendorpe, L., & Louveaux, J. (2007). Mimo relaying for multi-point to multi-point communication in wireless networks. In 2nd IEEE international workshop on computational advances in multi-sensor adaptive processing, 2007. CAMPSAP 2007, pp. 217–220.
Johnson, R. A. H. a C. R. (1991). Topics in matrix analysis. Cambridge, UK: Cambridge University Press.
Brewer, J. (1978). Kronecker products and matrix calculus in system theory. IEEE Transactions on Circuits and Systems, 25, 772–781.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of (15)
The pre-coded signals retransmitted by MIMO-relay is given by
where \({\varvec{\Omega }}(t)\in {\mathbb {C}}^{R\times 1}\), hence the total MIMO-relay transmit power can be calculated as
where the inner product for vectors \(\mathbf{x}(t),\mathbf{y}(t)\) is defined as
By using the correlation of the code-words defined in (5), the total relay transmit power can be written as
For simplicity, we represent \(\mathrm{Q}\) in (42) into the following quadratic form
The kernel of the above form can be expressed as a Kronecker products as follow
where \(\Upsilon \triangleq \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\rho _{1,1} }&{} {\rho _{1,2} }&{} {...}&{} {\rho _{1,d} } \\ {\rho _{2,1} }&{} \ddots &{} &{} \vdots \\ \vdots &{} &{} &{} \\ {\rho _{d,1} }&{} \cdots &{} &{} {\rho _{d,d} } \\ \end{array} }} \right] \).
Applying Lemma 1 to (42), the MIMO-Relay total transmit power (15) will be obtained.
Appendix B: Derivation of (18)
We can rewrite (11) as
The first term of the right hand side of the above formula can be expressed as
Then the correlation matrix of \({\varvec{\Gamma }}_{-\varepsilon _n}\) can be calculated as
where \((a)\) holds because \(s_n\) and \(s_l\) are uncorrelated for \(l\ne n, (b)\) holds because \(\left( {\mathbf{x}\otimes \mathbf{y}} \right) ^{H}=\mathbf{x}^{H}\otimes \mathbf{y}^{H}\) and \((c)\) holds because \(\left( {\mathbf{A}\otimes \mathbf{B}} \right) \left( {\mathbf{C}\otimes \mathbf{D}} \right) =\mathbf{AC}\otimes \mathbf{BD}\) for any conforming matrices \(\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\) reference [57].
By using the following definition
and using \({\varvec{\upvarepsilon }}_n = =\int \limits _{-\infty }^{\infty }u_n^{*}(t)\mathbf{v}(t)dt{\overset{\Delta }{=}}\left\langle {u_{n} \left( t \right) ,{\mathbf {v}}\left( t \right) } \right\rangle \) from (6) in the definition of (11), \({\varvec{\Gamma }}_{\varepsilon _n }\) can be written as
then the correlation of \({\varvec{\Gamma }}_{\varepsilon _n } \) is thus:
where \((a)\) holds because \(\left( {\mathbf{x}\otimes \mathbf{y}} \right) ^{H}=\mathbf{x}^{H}\otimes \mathbf{y}^{H},(b)\) holds because \(\left( {\mathbf{A}\otimes \mathbf{B}} \right) \left( {\mathbf{C}\otimes \mathbf{D}} \right) =\mathbf{AC}\otimes \mathbf{BD}\) for any conforming matrices \(\mathbf{A},\mathbf{B},\mathbf{C},\mathbf{D}\) [58] and \((c)\) holds because
As a result, the correlation matrix of \({\varvec{\Gamma }}\) will be obtained as
Appendix C: Derivation of (26)
From (11), \({\varvec{\Gamma }}_{-k} \) can be rewritten as
then the correlation of \({\varvec{\Gamma }}_{-k} \) i.e., \({\varvec{\upbeta }}_k \triangleq E\left( {{\varvec{\Gamma }}_{-k} {\varvec{\Gamma }}_{-k}^H } \right) \) can be easily constructed as below
Rights and permissions
About this article
Cite this article
Golbon-Haghighi, MH., Mahboobi, B. & Ardebilipour, M. Linear Pre-coding in MIMO–CDMA Relay Networks. Wireless Pers Commun 79, 1321–1341 (2014). https://doi.org/10.1007/s11277-014-1932-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-014-1932-7