Outage Analysis of LTE-A Femtocell Networks with Nakagami-$m$ Channels

Abstract

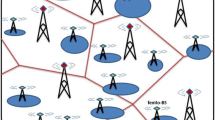
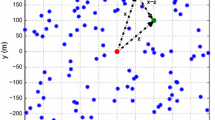
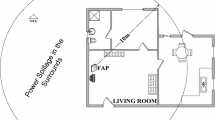
The concept of extending traditional macrocell cellular structure with small cells (like femtocells) in next-generation mobile networks (e. g., Long Term Evolution Advanced) provides a great opportunity to improve coverage and enhance data rate. Femtocells are cost efficient, indoor base stations. These femtocells can operate in closed mode i. e. only restricted users connection are allowed. Therefore, if the number of deployed femtocells is significant, that can dramatically modify the interference pattern of a macrocell. Thus mobile service providers have to pay attention for the number of simultaneously operating femtocells and encroach, if necessary, to provide appropriate service level to every mobile user. In this paper we provide an analytic framework to characterize the upper bound of service outage probability for a potential macrocell user in a two-tier mobile system, when the radio channels are infected by Nakagami-$m$ fading. In our proposal the femtocells are operating in closed mode and deployed into a designated macrocell, hence every femtocell increases the interference level. The spatial location femtocells is modelled with Poisson cluster process. Compared to traditional grid structure or completely spatial random Poisson point process femtocell deployment, cluster based layout may provides more life realistic deployment scenario. To evaluate the upper bound of service outage we use the tools of stochastic geometry.

Appendices

Appendix 1: Outage Probability for Non-group User in Case of Nakagami-$m$

It is known that in case of Nakagami-$m$ fading the amplitude ($x$) given in (5) follows Nakagami distribution and the received power $h_c=\frac{x^2}{\varOmega }$ follows Gamma distribution. It is assumed that $\varOmega =1$. Therefore, firstly we transform the random variable as follows. The new random variable is $y$ and we substitute

$$\begin{aligned} x=\sqrt{\frac{\varOmega T}{P^c g(\mathbf {z})}}\cdot \sqrt{y}\text {, hence }\frac{\text {d}x}{\text {d}y}=\frac{1}{2}\cdot \frac{\frac{\varOmega T}{P^c g(\mathbf {z})}}{\sqrt{\frac{\varOmega T y}{P^cg(\mathbf {z})}}}. \end{aligned}$$

Substituting this new random variable, the pdf modifies to:

$$\begin{aligned} f(y,m)=\frac{1}{\varGamma (m)}\left( \frac{Tm}{P^cg(\mathbf {z})} \right) ^m y^{m-1} \exp {\left( - \frac{mT}{P^cg(\mathbf {z})}\cdot y\right) }. \end{aligned}$$

Using the total probability law ${\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z})$ can be describe in the following form,

$$\begin{aligned} {\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z})&= {\mathsf {I}\!\mathsf {P}}\left\{ \frac{P^c h_c g(\mathbf {z})}{I(\mathbf {z})}\ge T \right\} ={\mathsf {I}\!\mathsf {P}}\left\{ I(\mathbf {z})\le \frac{P^c h_c g(\mathbf {z})}{T} \right\} \nonumber \\&= \int \limits _{y=0}^\infty f(y,m)\cdot \text {Pr}\left\{ I(\mathbf {z})\le y \right\} \text {d}y. \end{aligned}$$

(22)

Integration by parts equation (22) yields,

$$\begin{aligned} {\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z})&= \left[ \left( 1-\frac{\varGamma \left( m,\frac{mT}{P^cg(\mathbf {z})}\cdot y \right) }{\varGamma (m)}\right) \cdot \text {Pr}\left\{ I(\mathbf {z})\le y \right\} \right] _{y=0}^\infty \\&\quad -\int \limits _{y=0}^\infty \left( 1-\frac{\varGamma \left( m,\frac{mT}{P^cg(\mathbf {z})}\cdot y \right) }{\varGamma (m)} \right) \cdot \text {d}\left\{ \text {Pr}\big \{I(\mathbf {z})\le y \big \} \right\} , \end{aligned}$$

where $\varGamma \left( m,\frac{mT}{P^cg(\mathbf {z})}\cdot y \right)$ and $\varGamma (m)$ are the incomplete “lower” and standard (complete) gamma function, respectively. Using the well-known properties of Gamma function that $\varGamma (m,\infty )=0$ and in case of $m$ is an integer $\varGamma (m,0)=\varGamma (m)$ implies that:

$$\begin{aligned} {\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z}) =\int \limits _0^\infty \frac{\varGamma \left( m,\frac{mT}{P^cg(\mathbf {z})}\cdot y \right) }{\varGamma (m)}\text {d}\big \{\text {Pr}\left\{ I(\mathbf {z})\le y \right\} \big \}. \end{aligned}$$

Invoking the sum version of an incomplete gamma function:

$$\begin{aligned} \varGamma (s,x)=(s-1)! e^{-x} \sum _{k=0}^{s-1} \frac{x^k}{k!}~ \text {and}~ \varGamma (m)=(m-1)! ~\text { if} ~m ~\text {is integer}, \end{aligned}$$

provides the following form for coverage:

$$\begin{aligned} {\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z}) =\sum _{k=0}^{m-1}\frac{1}{k!}\int \limits _0^\infty \exp {\left( -\frac{Tm}{P^cg(\mathbf {z})}y\right) } \left( \frac{Tm}{P^cg(\mathbf {z})} y\right) ^k\text {d}\big \{\text {Pr}\left\{ I(\mathbf {z})\le y \right\} \big \}. \end{aligned}$$

(23)

The definition of Laplace transform and the $k$th order derivate is defined as follows,

$$\begin{aligned}&\displaystyle \fancyscript{L}_X(s) = \int \limits _0^\infty \exp {\left( -sx\right) }f_X(x) \text {d}x=\int \limits _0^\infty \exp {\left( -sx\right) }\text {d}\left\{ F_X(x)\right\} ,&\\&\displaystyle \frac{\text {d}^k}{\text {d} s^k}\fancyscript{L}_{X}(s)=(-1)^k\int \limits _0^\infty x^k\exp {\left( -sx\right) }\text {d}\left\{ F_X(x)\right\}&\end{aligned}$$

Finally, substituting the $k$th order derivate to the (23) concludes the proof:

$$\begin{aligned} {\mathsf {I}\!\mathsf {P}}\left\{ \text {coverage} \right\} (\mathbf{z}) = \sum _{k=0}^{m-1}\frac{(-1)^k}{k!}\left[ s^k \frac{\text {d}^k}{\text {d} s^k} \fancyscript{L}_{I(z)}(s) \right] \Bigg |_{s=\frac{Tm}{P^cg(\mathbf {z})}}. \end{aligned}$$

(24)

Appendix 2: Proof of Raw Moments

After calculating the fourth power of $\mathbb {E}_\mathbf{y}\left\{ \Vert \mathbf {x} +\mathbf {y}-\mathbf {z}\Vert ^4 \right\}$ we can apply the expectation operator for the monomials of the calculated polynomial. According to the properties of Thomas cluster process $\mathbf {y}$ follows normal distribution with zero mean and $\delta ^2$ variance. Let us introduce the definition of the $p$th (plain) moment of a normal random variable:

$$\begin{aligned} \mathrm {E}\left\{ \mathbf {y}^p\right\} = {\left\{ \begin{array}{ll} 0 &{} \text {if }p\text { is odd,} \\ \delta ^p\,(p-1)!! &{} \text {if }p\text { is even.} \end{array}\right. } \end{aligned}$$

Therefore substituting the plain moments into the polynomial, we get: $\mathbb {E}_\mathbf{y}\left\{ \Vert \mathbf {x}+\mathbf {y}-\mathbf {z}\Vert ^4 \right\} = 3\delta ^4+6\delta ^2\Vert \mathbf {x}-\mathbf {z}\Vert ^2+\Vert \mathbf {x}-\mathbf {z}\Vert ^4, \text {which is equals to} \left( \delta ^2 + \Vert \mathbf {x}-\mathbf {z}\Vert ^2\right) ^2+2\delta ^4+4\delta ^2\Vert \mathbf {x}-\mathbf {z}\Vert ^2$ and finishes the proof.