An Integration of Source and Jammer for a Decode-and-Forward Two-way Scheme Under Physical Layer Security

Abstract

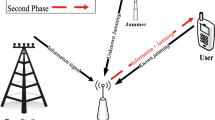
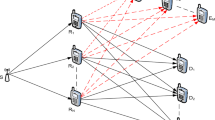
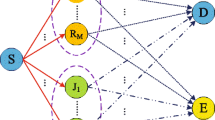
In this paper, we propose and analyze the integration of source and jammer for a decode-and-forward two-way scheme under physical layer security where the source nodes not only transmit data signals, but also transmit jamming signals to degrade the quality of eavesdropping links, and a selected relay forwards the combined data signals using an XOR operation. In this proposed protocol, the best relay is chosen by the maximum end-to-end achievable secrecy rate, and the secrecy system performance is evaluated by the exact and asymptotic secrecy outage probability over flat and block Rayleigh fading channels. The Monte-Carlo results are presented to verify the theoretical analysis.

Appendices

Appendix 1: Solving the CDF of RV $\textit{ASR}_1$ in Formula (25)

In the high SNR $\gamma$, $\textit{ASR}_1$ in (25) is rewritten as

$$\begin{aligned} {\textit{ASR}_1} = \min \left\{ {{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{11}^3}}{{1 + \frac{{b \omega _5^2}}{{\left( {1 - a} \right) \omega _4^2}} + \gamma {\omega _{31}}}}} \right) } \right] }^+ },{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{21}^3}}{{1 + \frac{{a \omega _4^1}}{{\left( {1 - b} \right) \omega _5^1}} + \gamma {\omega _{31}}}}} \right) } \!\right] }^+ }} \right\} \nonumber \\ \end{aligned}$$

(52)

Then, the CDF of $\textit{ASR}_1$ is expressed as

$$\begin{aligned} {F_{{\textit{ASR}_1}}}(x) = \Pr \left[ {{\textit{ASR}_1} < x} \right] = 1 - \Pr \left[ {{\textit{ASR}_1} \ge x} \right] \end{aligned}$$

(53)

Substituting (52) into (53), we obtain (54) as

$$\begin{aligned} {F_{{\textit{ASR}_1}}}(x)&= 1 - \Pr \left[ {{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{11}^3}}{{1 + \frac{{b\omega _5^2}}{{\left( {1 - a} \right) \omega _4^2}} + \gamma {\omega _{31}}}}} \right) } \right] }^+ }\right. \nonumber \\&\ge \left. x,{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{21}^3}}{{1 + \frac{{a\omega _4^1}}{{\left( {1 - b} \right) \omega _5^1}} + \gamma {\omega _{31}}}}} \right) } \right] }^+ } \ge x \right] \nonumber \\&= 1 - \Pr \left[ \omega _{11}^3 \ge \frac{{{2^{3x}} - 1}}{\gamma } + \frac{{{2^{3x}}b}}{{\gamma \left( {1 - a} \right) }}\left( {\frac{{\omega _5^2}}{{\omega _4^2}}} \right) + {2^{3x}}{\omega _{31}},\omega _{21}^3\right. \nonumber \\&\ge \left. \frac{{{2^{3x}} - 1}}{\gamma } + \frac{{{2^{3x}}a}}{{\gamma \left( {1 - b} \right) }}\left( {\frac{{\omega _4^1}}{{\omega _5^1}}} \right) +2^{3x}{\omega _{31}} \right] \end{aligned}$$

(54)

Set ${\theta _x} = {2^{3x}}$, ${p_x} = {{\left( {{2^{3x}} - 1} \right) } \big / \gamma }$, ${m_x} = {{\left( {{2^{3x}}a} \right) } \big / {\left( {\gamma \left( {1 - b} \right) } \right) }}$, ${n_x} = {{\left( {{2^{3x}}b} \right) } \big / {\left( {\gamma \left( {1 - a} \right) } \right) }}$, and ${Y_\xi } = \frac{{\omega _4^\xi }}{{\omega _5^\xi }},\,\xi \in \left\{ {1,2} \right\}$, then (54) is rewritten as

$$\begin{aligned} {F_{{\textit{ASR}_1}}}(x)&= 1 - \Pr \left[ {\omega _{11}^3 \ge {p_x} + \frac{{{n_x}}}{{{Y_2}}} + {\theta _x}{\omega _{31}},\,\,\omega _{21}^3 \ge {p_x} + {m_x}{Y_1} + {\theta _x}{\omega _{31}}} \right] \nonumber \\&= 1 - \int \limits _0^\infty {{f_{{\omega _{31}}}}(y)} \int \limits _0^\infty {{f_{{Y_1}}}(z)} \int \limits _0^\infty {{f_{{Y_2}}}(t)\left\{ {1 - {F_{\omega _{11}^3}}\left( {{p_x} + \frac{{{n_x}}}{t} + {\theta _x}y} \right) } \right\} } \nonumber \\&\times \, \left\{ {1 - {F_{\omega _{21}^3}}\left( {{p_x} + {m_x}z + {\theta _x}y} \right) } \right\} dtdzdy \end{aligned}$$

(55)

where ${f_{{\omega _{31}}}}(x)$, ${F_{\omega _{11}^3}}(x)$, ${F_{\omega _{21}^3}}(x)$ are the probability density functions (PDF) of the RV ${\omega _{31}}$, the CDF of the RVs $\omega _{11}^3$, and $\omega _{21}^3$ , respectively, and are given as

$$\begin{aligned} {f_{{\omega _{31}}}}(x)&= {\lambda _3}{e^{ - {\lambda _3}x}}\end{aligned}$$

(56)

$$\begin{aligned} {F_{\omega _{\xi 1}^3}}(x)&= 1 - {e^{ - {\lambda _\xi }x}},\,\,\quad \xi \in \left\{ {1,2} \right\} \end{aligned}$$

(57)

The CDF of ${Y_\xi }$ is given as

$$\begin{aligned} {F_{{Y_\xi }}}(z) = \Pr \left( {{Y_\xi } < z} \right) = \Pr \left( {\,\,\frac{{\omega _4^\xi }}{{\omega _5^\xi }} < z} \right) = \int \limits _0^\infty {{f_{\omega _5^\xi }}(y)\int \limits _0^{yz} {{f_{\omega _4^\xi }}(x)dxdy} } \end{aligned}$$

(58)

where ${f_{\omega _4^\xi }}(x)$ and ${f_{\omega _5^\xi }}(x)$ are the PDF of the exponential RVs $\omega _4^\xi$ and $\omega _5^\xi \,$, respectively, and are give as

$$\begin{aligned} {f_{\omega _\upsilon ^\xi }}(x) = {\lambda _\upsilon }{e^{ - {\lambda _\upsilon }x}},\quad \upsilon \in \left\{ {4,5} \right\} ,\,\quad \xi \in \left\{ {1,2} \right\} \end{aligned}$$

(59)

Substituting (59) into (58), we obtain (60) as

$$\begin{aligned} {F_{{Y_\xi }}}(z) = \int \limits _0^\infty {{\lambda _5}{e^{ - {\lambda _5}y}}\int \limits _0^{yz} {{\lambda _4}{e^{ - {\lambda _4}x}}dxdy = } } \frac{{{\lambda _4}z}}{{{\lambda _4}z + {\lambda _5}}} \end{aligned}$$

(60)

From ${F_{{Y_\xi }}}(z)$, the PDF of RV ${Y_\xi }$ is given as

$$\begin{aligned} {f_{{Y_\xi }}}(z) = \frac{{d{F_{{Y_\xi }}}(z)}}{{dz}} = \frac{{{\lambda _4}{\lambda _5}}}{{{{\left( {{\lambda _4}z + {\lambda _5}} \right) }^2}}} \end{aligned}$$

(61)

Substituting (56), (57) and (61) into (55), and after some manipulations, the CDF of $\textit{ASR}_1$ is obtained as

$$\begin{aligned} {F_{{\textit{ASR}_1}}}(x)&= 1 - \frac{{{\lambda _1}{\lambda _2}{\lambda _3}{m_x}{n_x}{e^{ - {p_x}\left( {{\lambda _1} + {\lambda _2}} \right) }}{e^{{{{\lambda _1}{\lambda _4}{n_x}} / {{\lambda _5} + {{{\lambda _2}{\lambda _5}{m_x}} / {{\lambda _4}}}}}}}}}{{{\lambda _3} + {\theta _x}\left( {{\lambda _1} + {\lambda _2}} \right) }}\nonumber \\&\times \, \varGamma \left[ { - 1,{{{\lambda _1}{\lambda _4}{n_x}} \big / {{\lambda _5}}}} \right] \times \varGamma \left[ { - 1,{{{\lambda _2}{\lambda _5}{m_x}} \big / {{\lambda _4}}}} \right] \end{aligned}$$

(62)

where $\varGamma \left[ {a,z} \right]$ is the incomplete gamma function and is defined as $\varGamma (a,z) = \mathop \int \nolimits _z^\infty {t^{a - 1}}{e^{ - t}}dt$ [25, Eq. (8.350.2)].

Appendix 2: Solving the CDF of RV $\textit{ASR}_i$ in Formula (41)

The CDF of RV $\textit{ASR}_i$, $i = \left\{ {1,2,\ldots ,M} \right\}$, is given from (41) as

$$\begin{aligned} {F_{{\textit{ASR}_i}}}(x)&= \Pr \left[ {{\textit{ASR}_i} < x} \right] \nonumber \\&= \Pr \left[ {\min \left\{ {{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{1i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ },{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{2i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ }} \right\} < x} \right] \nonumber \\&= 1 - \Pr \left[ {\min \left\{ {{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{1i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ },\,{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{2i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ }} \right\} \ge x} \right] \,\nonumber \\&= 1 - \Pr \left[ {{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{1i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ } \ge x,\,{{\left[ {\frac{1}{3}{{\log }_2}\left( {\frac{{1 + \gamma \omega _{2i}^3}}{{1 + \gamma {\omega _{3i}}}}} \right) } \right] }^+ } \ge x} \right] \end{aligned}$$

(63)

After some manipulations of (63), the CDF of $\textit{ASR}_i$ is obtained as

$$\begin{aligned} {F_{{\textit{ASR}_i}}}(x)&= 1 - \Pr \left[ {\omega _{1i}^3 \ge {p_x} + {\theta _x}{\omega _{3i}}\,,\,\omega _{2i}^3 \ge {p_x} + {\theta _x}{\omega _{3i}}} \right] \,\nonumber \\&= 1 - \int \limits _0^\infty {{f_{{\omega _{3i}}}}(y)\left\{ {1 - {F_{\omega _{1i}^3}}\left( {{p_x} + {\theta _x}y} \right) } \right\} } \left\{ {1 - {F_{\omega _{2i}^3}}\left( {{p_x} + {\theta _x}y} \right) } \right\} dy \end{aligned}$$

(64)

where ${f_{{\omega _{3i}}}}(x)$, ${F_{\omega _{1i}^3}}(x)$, ${F_{\omega _{2i}^3}}(x)$ are the PDF of the RV ${\omega _{3i}}$, the CDF of the RVs $\omega _{1i}^3$ and $\omega _{2i}^3$, $i = \left\{ {1,2,\ldots ,M} \right\}$, respectively, and are obtained as same as (56) and (57).

Then, CDF of $\textit{ASR}_i$ is obtained as

$$\begin{aligned} {F_{{\textit{ASR}_i}}}(x) = 1 - \frac{{{\lambda _3}{e^{ - {p_x}\left( {{\lambda _1} + {\lambda _2}} \right) }}}}{{{\lambda _3} + {\theta _x}\left( {{\lambda _1} + {\lambda _2}} \right) }} \end{aligned}$$

(65)

Appendix 3: Solving Formula (49)

In the high SNR $\gamma$, (49) is rewritten as

$$\begin{aligned} P_{CC}^{{x_1}}&= \underbrace{\Pr \left[ {\left( {1 - b} \right) \omega _5^1 \ge a{\theta _{{R_0}{R_0}}}\omega _4^1,\,a\gamma \omega _4^1 + \gamma {\omega _{31}} \ge {\theta _{{R_0}{R_0}}}} \right] }_{{I_1}}\nonumber \\&+\, \underbrace{\Pr \left[ {{Y_1} > \underbrace{{{\left( {1 - b} \right) } \big / {\left( {a{\theta _{{R_0}{R_0}}}} \right) }}}_{{y_0}},{\omega _{31}} \ge \frac{a}{{\gamma \left( {1 - b} \right) }} \times \left( {\underbrace{{{{\theta _{{R_0}{R_0}}}\left( {1 - b} \right) } \big / a}}_{{y_1}} - {Y_1}} \right) } \right] }_{{I_2}}\nonumber \\ \end{aligned}$$

(66)

The first component in (66) is given as

$$\begin{aligned} {I_1}&= \int \limits _{{{{\theta _{{R_0}{R_0}}}} / {\left( {a\gamma } \right) }}}^\infty {{f_{\omega _4^1}}(x)\left\{ {1 - {F_{\omega _5^1}}\left( {\frac{{a{\theta _{{R_0}{R_0}}}x}}{{\left( {1 - b} \right) }}} \right) } \right\} dx} \nonumber \\&+\, \int \limits _0^{{{{\theta _{{R_0}{R_0}}}} / {\left( {a\gamma } \right) }}} {{f_{\omega _4^1}}(x)\left\{ {1 - {F_{\omega _5^1}}\left( {\frac{{a{\theta _{{R_0}{R_0}}}x}}{{\left( {1 - b} \right) }}} \right) } \right\} \left\{ {1 - {F_{{\omega _{31}}}}\left( {\frac{{{\theta _{{R_0}{R_0}}} - a\gamma x}}{\gamma }} \right) } \right\} dx}\qquad \quad \end{aligned}$$

(67)

where ${F_{\omega _5^1}}(x)$ and ${F_{{\omega _{31}}}}(x)$ are the CDF of the exponential RVs $\omega _5^1$ and ${\omega _{31}}$, respectively, and are given as ${F_{\omega _5^1}}(x) = 1 - {\lambda _5}{e^{ - {\lambda _5}x}}$ and ${F_{{\omega _{31}}}}(x) = 1 - {\lambda _3}{e^{ - {\lambda _3}x}}$.

Hence, after some manipulations, the first component in (66) is solved as

$$\begin{aligned} {I_1}&= \frac{{{\lambda _4}{e^{{{ - {\theta _{{R_0}{R_0}}}\left( {{\lambda _4} + {{a{\lambda _5}{\theta _{{R_0}{R_0}}}} / {\left( {1 - b} \right) }}} \right) } / {\left( {a\gamma } \right) }}}}}}{{{\lambda _4} + {{a{\lambda _5}{\theta _{{R_0}{R_0}}}} / {\left( {1 - b} \right) }}}}\nonumber \\&+\, \frac{{{\lambda _4}{e^{{{ - {\lambda _3}{\theta _{{R_0}{R_0}}}} / \gamma }}}}}{{{\lambda _4} + {{a{\lambda _5}{\theta _{{R_0}{R_0}}}} / {\left( {1 - b} \right) - a{\lambda _3}}}}}\left\{ {1 - {e^{{{ - {\theta _{{R_0}{R_0}}}\left( {{\lambda _4} + {{a{\lambda _5}{\theta _{{R_0}{R_0}}}} / {\left( {1 - b} \right) - a{\lambda _3}}}} \right) } / {\left( {a\gamma } \right) }}}}} \right\} \qquad \quad \end{aligned}$$

(68)

The second component in (66) is given as

$$\begin{aligned} {I_2}&= \Pr \left[ {{Y_1} > {y_0},{\omega _{31}} \ge \frac{a}{{\gamma \left( {1 - b} \right) }} \times \left( {{y_1} - {Y_1}} \right) } \right] \nonumber \\&= \int \limits _{\max ({y_0},{y_1})}^\infty {{f_{{Y_1}}}(x)dx} + {\left[ {\int \limits _{{y_0}}^{{y_1}} {{f_{{Y_1}}}(x)\left\{ {1 - {F_{{\omega _{31}}}}\left( {\frac{{a\left( {{y_1} - x} \right) }}{{\gamma \left( {1 - b} \right) }}} \right) } \right\} } } \right] ^+ } \end{aligned}$$

(69)

Substituting (61) into (69), after some manipulations, we obtained as

$$\begin{aligned} {I_2}&= \frac{{{\lambda _5}}}{{{\lambda _4}\max ({y_0},{y_1}) + {\lambda _5}}} + {\lambda _4}{\lambda _5}{e^{ - {{{\lambda _3}{\theta _{{R_0}{R_0}}}} / \gamma }}}\nonumber \\&\times \, {\left[ \begin{array}{l} \frac{{{e^{{{a{\lambda _3}{y_0}} / {\left( {\gamma \left( {1 - b} \right) } \right) }}}}}}{{{\lambda _4}\left( {{\lambda _4}{y_0} + {\lambda _5}} \right) }} - \frac{{{e^{{{a{\lambda _3}{y_1}} / {\left( {\gamma \left( {1 - b} \right) } \right) }}}}}}{{{\lambda _4}\left( {{\lambda _4}{y_1} + {\lambda _5}} \right) }} - \frac{{a{\lambda _3}{e^{{{a{\lambda _3}{\lambda _5}} / {\left( {\gamma \left( {1 - b} \right) {\lambda _4}} \right) }}}}}}{{\gamma \left( {1 - b} \right) \lambda _4^2}}\\ \times \left\{ {Ei\left[ {\frac{{a{\lambda _3}}}{{\gamma \left( {1 - b} \right) }}\left( {{y_0} + {{{\lambda _5}} / {{\lambda _4}}}} \right) } \right] - Ei\left[ {\frac{{a{\lambda _3}}}{{\gamma \left( {1 - b} \right) }}\left( {{y_1} + {{{\lambda _5}} / {{\lambda _4}}}} \right) } \right] } \right\} \end{array} \right] ^+ } \end{aligned}$$

(70)

where $Ei[x]$ is the exponential integral function, $Ei(x) = - \int _{ - x}^\infty {\left( {{{{e^{ - t}}} \big / t}} \right) } dt$, [25, Eq. (8.211.1)].

Substituting (68) and (70) into (66), we obtains the probability of the correct computation of the secrecy packet $x_1$ as in (50).