Effect of Network Coding and Multi-packet Reception on Point-to-Multi-point Broadcast Networks

Abstract

This paper addresses throughput and delay gains resulting from network coding (NC) used to complement multi-packet reception (MPR) in a single-relay multi-user wireless network in saturated and non-saturated traffic conditions. The cross-layer analytical framework is presented in analyzing the performance of the encode-and-forward (EF) relaying wireless networks, where employed at the physical layer under the conditions of unsaturated traffic and finite-length queue at the data link layer. Considering the characteristics of EF relaying protocol at the physical layer, first a model of a two-hop EF relaying wireless channel is proposed as an equivalent extended multi-dimensional Markovian state transition model in queuing analysis. We show that the initial transmissions and the back-filling process can be greatly sped up through a combination of NC and MPR. We provided closed-form expressions for two-hop unbalanced bidirectional traffic cases both with and without NC even if the buffers on nodes are unsaturated. The analytical results are mainly derived by solving queuing systems for the buffer behavior at the relay node. The model has been evaluated through simulations and in comparison with the existing analytical model. Simulation results show good agreement with the analytical results.

Appendices

Appendix 1: Proof of Lemma 1

Proof

The sum of steady-state probabilities $Q(0), Q(1*)$ and $Q(2*)$ and the ratio of the steady-state probabilities $Q(1*)$ to $Q(2*)$ are proportional:

$$\begin{aligned} Q(0) + Q(1*) + Q(2*) = 1,\quad \frac{Q(1*)}{Q(2*)} = \frac{(\lambda _1+\lambda _{1,2})}{(\lambda _2+\lambda _{2,1})}\frac{\mu _2}{\mu _1} = \frac{\rho _1}{\rho _2}. \end{aligned}$$

(34)

where $Q(v*) = \sum _{\mathcal {V}_1^n\in \{1,2\}^n} Q(v\mathcal {V}_1^n)$

By solving equations in 34,

$$\begin{aligned} Q(v*) = \frac{\rho _v}{\rho _1 + \rho _2}(1-Q(0)). \end{aligned}$$

(35)

The arrival rate $\lambda _R$ in relay node $\mathbf {R}$ and the departure rate $\mu _R$ from relay node $\mathbf {R}$ are balanced in steady-state. They are expressed as:

$$\begin{aligned} \lambda _R&= (\lambda _{0,1} + \lambda _{0,2}+\lambda _{1,2}+\lambda _{2,1})Q(0) + (\lambda _1 + \lambda _2+\lambda _{1,2}+\lambda _{2,1})(1-Q(0)) \nonumber \\&= (\lambda _1 + \lambda _2+\lambda _{1,2}+\lambda _{2,1})\bigg [\frac{1-\tau _R(1-Q(0))}{1-\tau _R}\bigg ], \nonumber \\ \mu _R&= \mu _1Q(1*) + \mu _2Q(2*) = (\lambda _1 + \lambda _2+\lambda _{1,2}+\lambda _{2,1})\frac{(1-Q(0))}{\rho _1 + \rho _2}, \nonumber \\ \mu _R&= \lambda _R \Rightarrow Q(0) = \frac{(1-\tau _R)(1-\rho _1 - \rho _2)}{(1-\tau _R) + \tau _R(\rho _1 + \rho _2)}. \end{aligned}$$

(36)

We can calculate the relation between $Q(1\mathcal {V}_1^n)$ and $Q(2\mathcal {V}_1^n)$ as Eq. and apply the detailed balance equations in ascending order of queue state length obtaining these results:

$$\begin{aligned} \frac{Q(1\mathcal {V}_1^n)}{Q(2\mathcal {V}_1^n)}&= \frac{\rho _1}{\rho _2}, \nonumber \\ (\lambda _{0,1} + \lambda _{0,2}+\lambda _{1,2}+\lambda _{2,1})Q(0)&= \mu _1Q(1) + \mu _2Q(2),\nonumber \\ (\lambda _1 + \lambda _2+\lambda _{1,2}+\lambda _{2,1})Q(\mathcal {V}_1^n)&= \mu _1Q(1\mathcal {V}_1^n) + \mu _2Q(2\mathcal {V}_1^n). \end{aligned}$$

(37)

By applying these equations, the following lemma is obtained.

Appendix 2: Proof of Lemma 2

Proof

From 7, the steady-state probability $P_v(0)$ can be expressed as:

$$\begin{aligned} P_v(0) = Q(0) + \sum _{n_{\bar{v}}=1}^\infty \frac{\rho _{\bar{v}}^{n_{\bar{v}}}Q(0)}{(1-\tau _R)} = Q(0)\bigg [ \frac{1-\tau _R(1-\rho _{\bar{v}})}{(1-\tau _R)(1-\rho _{\bar{v}})}\bigg ] . \end{aligned}$$

(38)

From 7, the steady-state probabilities $P(n)$ after some algebra can be expanded as:

$$\begin{aligned} P(n) =\sum _{\mathcal {V}_1^n\in \{1,2\}^n} Q(\mathcal {V}_1^n) = \frac{(\rho _1 + \rho _2)^n}{(1-\tau _R)}P(0); n>0 , P(0) = Q(0). \end{aligned}$$

(39)

Appendix 3: Proof of Lemma 3

Proof

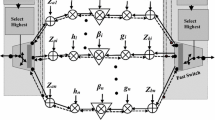
It is assumed that the steady-state probability $P(0,0)$ is positive, i.e. both virtual queues are non-saturated. Figure 14 illustrates the Markov chain with respect to the number of packets in virtual queue $v$ at relay node $\mathbf {R}$. The state transition probability from states 0 to 1 is equal to:

$$\begin{aligned} \lambda _{2,v} = \lambda _v\bigg ( 1-\frac{P(0,0)}{P_v(0)}\bigg ) + \lambda _{0,v}\frac{P(0,0)}{P_v(0)}+\lambda _{1,1}. \end{aligned}$$

(40)

The detailed balance equations are obtained as follows:

$$\begin{aligned} P_v(1)&= \rho _vP_v(0) + \frac{\rho _v\tau _R}{1-\tau _R}P(0,0), \nonumber \\ P_v(n+1)&= \rho _vP_v(n); n\ge 1. \end{aligned}$$

(41)

where $\rho _v= \frac{\lambda _{0,v}+\lambda _{1,1}}{\mu _v}$.

Summing all the steady-state probabilities $P_v(n)$ , the normalized condition and some algebra enable us to obtain Lemma 3 as follows: $\sum _{n=0}^\infty P_v(n) = 1 \Rightarrow \frac{P_v(0)(1-\tau _R)+\rho _v\tau _RP(0,0)}{(1-\rho _v)(1-\tau _R)} = 1$.

Fig. 14

The Markov chain with respect to the number of packets in virtual queue $v$ at relay node $\mathbf {R}$ in the NC-CSMA/CA protocol

Appendix 4: Proof of Lemma 4

Proof

Based on Fig. 5, we can express the detailed balance equation as follows:

$$\begin{aligned} P(1,0)&= \frac{\rho _1}{1-\tau _R}P(0,0), P(0,1) = \frac{\rho _2}{1-\tau _R}P(0,0), \nonumber \\ P(n_1+1,n_2)&= \rho _1P(n_1,n_2), P(n_1,n_2+1) = \rho _2P(n_1,n_2), \end{aligned}$$

(42)

for any $(n_1,n_2)\ne (0,0)$. The above detailed balance equations provide:

$$\begin{aligned} P(n_1,n_2) = \frac{\rho _1^{n_1}\rho _2^{n_2}}{1-\tau _R}P(0,0). \end{aligned}$$

(43)

for any $(n_1,n_2)\ne (0,0)$.

Summing all the steady-state probabilities $P(n_1,n_2)$, which are functions of $P(0,0)$, and the normalized condition enable us to obtain

$$\begin{aligned} 1&= \sum _{n_1=0}^\infty \sum _{n_2=0}^\infty P(n_1,n_2) = \frac{P(0,0)}{1-\tau _R} \left( \sum _{n_1=0}^\infty \sum _{n_2=0}^\infty \rho _1^{n_1}\rho _2^{n_2}-\tau _R\right) \nonumber \\&= \frac{1-\tau _R(1-\rho _1)(1-\rho _2)}{(1-\tau _R)(1-\rho _1)(1-\rho _2)}P(0,0). \end{aligned}$$

(44)

and then an approximate expression of $P(0,0)$ is derived as

$$\begin{aligned} P(0,0) = \frac{(1-\tau _R)(1-\rho _1)(1-\rho _2)}{1-\tau _R(1-\rho _1)(1-\rho _2)} \end{aligned}$$

Appendix 5: Proof of Proposition 1

Proof

First, we note the following relations:

$$\begin{aligned} \pi _{i,0}&= P_{eq}\pi _{i-1,0}=P_{eq}^i\pi _{0,0},\quad 1\le i\le m.\end{aligned}$$

(45)

$$\begin{aligned} \pi _{i,k}&= \frac{W_i-k}{P_dW_i}P_{eq}^i\pi _{0,0},\quad 0\le i\le m, 1\le k\le W_i-1. \end{aligned}$$

(46)

The stationary probability to be in state $\pi _I$ can be evaluated as follows:

$$\begin{aligned} \pi _I=\pi _I(1-q)+\pi _{m,0}(1-q)P_{eq}+(1-q)(1-P_{eq})\sum _{i=0}^m\pi _{i,0} \Rightarrow \pi _I= \frac{1-q}{q}\pi _{0,0}. \end{aligned}$$

(47)

Employing the normalization condition, after some mathematical manipulations, and remembering the relation $\sum _{i=0}^m\pi _{i,0} = \pi _{0,0}\frac{1-P_{eq}^{m+1}}{1-P_{eq}}$, it is possible to obtain:

$$\begin{aligned}&\sum \limits _{i=0}^m\sum \limits _{k=0}^{W_i-1}\pi _{i,k} +\pi _I = 1,\nonumber \\&\sum \limits _{k=1}^{W_i-1}\pi _{i,k} = \frac{P_{eq}^i\pi _{0,0}}{2P_d}(W_i-1),\nonumber \\&\sum \limits _{i=0}^m\frac{P_{eq}^i\pi _{0,0}}{2P_d}(2^iW-1) =\frac{\pi _{0,0}}{2P_d} \bigg (\frac{W(1-(2P_{eq})^{m+1})}{1-2P_{eq}} - \frac{(1-P_{eq}^{m+1})}{1-P_{eq}}\bigg ).\end{aligned}$$

(48)

$$\begin{aligned}&\sum \limits _{i=0}^m\sum \limits _{k=0}^{W_i-1}\pi _{i,k} = \sum \limits _{i=0}^m\sum \limits _{k=1}^{W_i-1}\pi _{i,k}+\sum \limits _{i=0}^m\pi _{i,0} \nonumber \\&\quad =\frac{\pi _{0,0}}{2P_d} \bigg (\frac{W(1-(2P_{eq})^{m+1})}{1-2P_{eq}} + \frac{(2P_d-1)(1-P_{eq}^{m+1})}{1-P_{eq}}\bigg ). \end{aligned}$$

(49)

The normalization condition yields the following equation for computation of $\pi _{0,0}$:

$$\begin{aligned} \pi _{0,0} =\frac{2qP_d(1-P_{eq})(1-2P_{eq})}{2P_d(1-q)(1-P_{eq})(1-2P_{eq})+qW(1-P_{eq})(1-(2P_{eq})^{m+1})+q(1-2P_{eq})(2P_d-1)(1-P_{eq}^{m+1})}.\nonumber \\ \end{aligned}$$

(50)

Equation 50 is then used to compute $\tau$ , the probability that a station starts a transmission in a randomly chosen time slot. In fact, taking into account that a packet transmission occurs when the back-off counter reaches zero, we have:

$$\begin{aligned} \tau&= \sum _{i=0}^m\pi _{i,0} = \pi _{0,0}\frac{1-P_{eq}^{m+1}}{1-P_{eq}} \nonumber \\&= \frac{2qP_d(1-P_{eq}^{m+1})(1-2P_{eq})}{2P_d(1-q)(1-P_{eq})(1-2P_{eq})+qW(1-P_{eq})(1-(2P_{eq})^{m+1})+q(1-2P_{eq})(2P_d-1)(1-P_{eq}^{m+1})}.\nonumber \\ \end{aligned}$$

(51)

Appendix 6: Proof of Proposition 2

Proof

According to Fig. 7, there are three durations that the considered node spends at a particular back-off state, $D_I$, $D_S$ and $D_C$. In the idle state, the considered node waits one time slot before decrementing the back-off counter. When the considered node enters successful state we can compute the duration in this state as follows:

$$\begin{aligned} D_S= \frac{1}{1-p_{ss}}T_{suce}+ \frac{p_{si}}{1-p_{ss}}D_I + \frac{p_{sc}}{1-p_{ss}}D_S, \end{aligned}$$

(52)

where $D_I=1$. Similarly, when the node enters a back-off state and finds the channel busy with a collision, this duration can be expressed as:

$$\begin{aligned} D_C= \frac{1}{1-p_{cc}}\overline{T_{coll}} + \frac{p_{cs}}{1-p_{cc}}D_S + \frac{p_{ci}}{1-p_{cc}}D_I. \end{aligned}$$

(53)

Let us consider the two cases in detail to calculate the average slot duration for each case:

• Entering from a previous back-off state: The average slot duration in this case can be expressed using $P_d$ as

  $$\begin{aligned} D_1 = \frac{1}{P_{d}}(p_{ei}D_I+p_{es}D_S+ p_{ec}D_C). \end{aligned}$$

  (54)

• Entering from a transmission state: In this case we can compute the average slot duration as follows

  $$\begin{aligned} D_2 = \frac{\overline{CW}-1}{q\overline{CW}}(p_{ei}D_I+p_{es}D_S+ p_{ec}D_C). \end{aligned}$$

  (55)

Then we can compute the average slot duration as $\mathcal {D} = (1-\tau )D_1 + \tau D_2.$