Prioritized Medium Access Control in Cognitive Radio Ad Hoc Networks: Protocol and Analysis

Abstract

Cognitive radio (CR) technology enables opportunistic exploration of unused licensed channels. By giving secondary users (SUs) the capability to utilize the licensed channels (LCs) when there are no primary users (PUs) present, the CR increases spectrum utilization and ameliorates the problem of spectrum shortage. However, the absence of a central controller in CR ad hoc network (CRAHN) introduces many challenges in the efficient selection of appropriate data and backup channels. Maintenance of the backup channels as well as managing the sudden appearance of PUs are critical issues for effective operation of CR. In this paper, a prioritized medium access control protocol for CRAHN, PCR-MAC, is developed which opportunistically selects the optimal data and backup channels from a list of available channels. We also design a scheme for reliable switching of a SU from the data channel to the backup channel and vice-versa. Thus, PCR-MAC increases network throughput and decreases SUs’ blocking rate. We also develop a Markov chain-based performance analysis model for the proposed PCR-MAC protocol. Our simulations, carried out in $NS-3$, show that the proposed PCR-MAC outperforms other state-of-the-art opportunistic medium access control protocols for CRAHNs.

Appendices

Appendix 1: Transition Probabilities

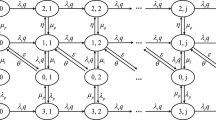
In this appendix, we derive the mathematical formulas for calculating the transition rates of Sect. 5.

$$\begin{aligned} \gamma _{(i, j+1, k, l, m+1, n)}^{(i, j, k, l, m, n)} = \delta _{6} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{6}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j+m) < c_1, (k+l+n) = c_2\\ 0,&{}\text { otherwise} \end{array}\right. \\ \gamma _{(i, j+1, k, l, m, n+1)}^{(i, j, k, l, m, n)}&= \delta _{7} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{7}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j+m) < c_1, k+l+m < c_2 \\ 0,&{} \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j+1, k, l, m-1, n+1)}^{(i, j, k, l, m, n)}&= \delta _{8} \cdot \lambda _{2} + \delta _{9} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{8}&= \left\{ \begin{array}{ll} 1,&{}\text { if, }(i+j+m) = c_1, (k+l+m+1) = c_2\\ 0,&{} \text { otherwise}\\ \end{array} \right. \end{aligned}$$

$\delta _{9}$ is same as $\delta _{8}$.

$$\begin{aligned} \gamma _{(i, j+1, k, l, m-1, n+2)}^{(i, j, k, l, m, n)} = \delta _{10} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{10}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j+m) = c_1, (k+l+n) < c_2\\ 0,&{}\text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k+1, l, m, n)}^{(i, j, k, l, m, n)}&= \delta _{11} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{11}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j) = c_1, (k+l+m) < c_2 \\ 0, &{}\text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k+1, l, m, n-1)}^{(i, j, k, l, m, n)}&= \delta _{12} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{12}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j) = c_1, (k+l+n) = c_2 \\ 0,&{} \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l+1, m, n)}^{(i, j, k, l, m, n)}&= \frac{c_2-k-l-n}{c_2-k-l} \cdot \lambda _{3} + \frac{n}{c_2-k-l} \cdot \lambda _{3} \cdot \delta _{13}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{13}&= \left\{ \begin{array}{ll} 1,&{} \text { if, } (k+l+n) < c_2\\ 0,&{} \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l+1, m, n-1)}^{(i, j, k, l, m, n)}&= \frac{n}{c_2-k-l} \cdot \delta _{14} \cdot \lambda _{3}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{14}&= \left\{ \begin{array}{ll} 1,&{} \text { if,} (i+j+m) = c_1, (k+l+n) = c_2 \\ 0,&{}\text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l+1, m+1, n-1)}^{(i, j, k, l, m, n)}&= \frac{n}{c_2-k-l} \cdot \delta _{15} \cdot \lambda _{3}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{15}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j+m) < c_1, (k+l+n) = c_2 \\ 0,&{} \text { otherwise} \\ \end{array}\right. \\ \gamma _{(i, j+1, k-1, l, m, n+1)}^{(i, j, k, l, m, n)}&= \delta _{16} \cdot \lambda _{4}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{16}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (i+j+m) < c_1, (k+l+n) \le c_2\\ 0,&{} \text { otherwise} \\ \end{array}\right. \\ \end{aligned}$$

$$\begin{aligned} \gamma _{(i-1, j, k, l, m, n)}^{(i, j, k, l, m, n)}&= i \cdot \mu _{1}, \\ \gamma _{(i, j-1, k, l, m, n)}^{(i, j, k, l, m, n)}&= j \cdot \frac{j-(m+n)}{j} \cdot \mu _{2}, \\ \gamma _{(i, j-1, k, l, m-1, n)}^{(i, j, k, l, m, n)}&= j \cdot \frac{m}{j} \cdot \mu _{2}\\ \gamma _{(i, j-1, k, l, m, n-1)}^{(i, j, k, l, m, n)}&= j \cdot \frac{n}{j} \cdot \mu _{2},\\ \gamma _{(i, j, k-1, l, m, n)}^{(i, j, k, l, m, n)}&= k \cdot \mu _{2}, \\ \gamma _{(i, j, k, l-1, m, n)}^{(i, j, k, l, m, n)}&= l \cdot \mu _{3}, \\ \gamma _{(i, j, k, l, m, n)}^{(i+1, j, k, l, m, n)}&= (i+1) \cdot \mu _{1},\\ \gamma _{(i, j, k, l, m, n)}^{(i, j+1, k, l, m, n)}&= (j+1) \cdot \frac{(j+1)-(m+n)}{j+1} \cdot \mu _{2}, \\ \gamma _{(i, j, k, l, m, n)}^{(i, j+1, k, l, m+1, n)}&= (j+1) \cdot \frac{m+1}{j+1} \cdot \mu _{2}.\\ \gamma _{(i, j, k, l, m, n)}^{(i, j+1, k, l, m, n+1)}&= (j+1) \cdot \frac{n+1}{j+1} \mu _{2}, \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k+1, l, m, n)}&= (k+1) \cdot \mu _{2}, \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k, l+1, m, n)}&= (k+1) \cdot \mu _{2},\\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k, l+1, m, n)}&= (l+1) \cdot \mu _{3},\\ \gamma _{(i, j, k, l, m, n)}^{(i-1, j, k, l, m, n)}&= \frac{c_1-(i-1)-j-m}{c_1-(i-1)} \cdot \lambda _{1} + \frac{m}{c_1-(i-1)} \cdot \lambda _{1} \cdot \delta _{17}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{17}&= \left\{ \begin{array}{ll} 1,\text { if, } (k+l+n) = c_2, (i-1)+j+m < c_1\\ 0, \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m, n)}&= \lambda _{2} \cdot \delta _{18}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{18}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } (k+l+n) = c_2, i+(j-1)+m+1 = c_1 \\ 0,&{} \text { otherwise} \\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m-1, n)}&= \lambda _{2} \cdot \delta _{19}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{19}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } i+(j-1)+(m-1)+2 \le c_1, (k+l+n) = c_2 \\ 0,&{}\text { otherwise} \\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m, n-1)}&= \lambda _{2} \cdot \delta _{20}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{20}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } i+(j-1)+m < c_1, k+l+(n-1)<c_2 \\ 0,&{}\text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k-1, l, m, n)}&= \lambda _{2} \cdot \delta _{21}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{21}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } i+j = c_1, (k-1)+l+n < c_2 \\ 0,&{} \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k, l-1, m, n)}&= \frac{c_2-k-(l-1)-n}{c_2-k-(l-1)} \cdot \lambda _{3}. \\ \gamma _{(i, j, k, l, m, n)}^{(i-1, j, k, l, m+1, n)}&= \frac{m+1}{c_1-(i-1)} \cdot \lambda _{1} \cdot \delta _{22} + \frac{j}{c_1-(i-1)} \cdot \frac{m}{m+n} \cdot \lambda _{1}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{22}&= \left\{ \begin{array}{ll} 1,\text { if, } (i-1)+j+m = c_1, k+l+n = c_2\\ 0, \text {otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i-1, j, k, l, m+1, n-1)}&= \frac{m+1}{c_1-(i-1)} \cdot \lambda _{1} \cdot \delta _{23}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{23}&= \left\{ \begin{array}{ll} 1,\text { if, } k+l+(n-1) < c_2 \\ 0, \text { otherwise }\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i-1, j+1, k, l, m, n)}&= \frac{j+1}{c_1-(i-1)} \cdot \frac{(j+1)-(m+n)}{(m+n)} \cdot \lambda _{1},\\ \gamma _{(i, j, k, l, m, n)}^{(i-1, j+1, k-1, l, m, n+1)}&= \frac{j+1}{C1-(i-1)} \cdot \frac{m+1}{m+(n+1)} \cdot \lambda _{1} \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m+1, n-1)}&= \lambda _{2} \cdot \delta _{24} + \lambda _{2} \cdot \delta _{25}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{24} = \left\{ \begin{array}{ll} 1,\text { if, }i+(j-1)+(m+1)= c_1, k+l+(n-1)+1 = c_2\\ 0, \text { otherwise}\\ \end{array} \right. \\ \end{aligned}$$

$\delta _{25}$ is same as $\delta _{24}$.

$$\begin{aligned} \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m+1, n-2)} = \lambda _{2} \cdot \delta _{26}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{26}&= \left\{ \begin{array}{ll} 1,\text { if, } i+(j-1)+(m+1)= c_1, k+l+(n-2) < c_2 \\ 0, \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k+1, l, m, n-1)}&= \delta _{27} \cdot \lambda _{4}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{27}&= \left\{ \begin{array}{ll} 1,\text { if, } i+(j-1)+m < c_1, (k+1)+l+(n-1) < c_2 \\ 0, \text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j-1, k, l, m+1, n)}&= \delta _{28} \cdot \lambda _{2}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{28}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } i+(j-1)+(m+1) = c_1, k+l+n = c_2\\ 0,&{}\text { otherwise}\\ \end{array} \right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k, l-1, m, n+1)}&= \frac{n+1}{c_2-k-(l-1)} \cdot \delta _{29} \cdot \lambda _{3}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{29}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } i+j+m = c_1, k+(l-1)+(m+1) = c_2 \\ 0,&{}\text { otherwise}\\ \end{array}\right. \\ \gamma _{(i, j, k, l, m, n)}^{(i, j, k, l-1, m-1, n+1)}&= \frac{n+1}{c_2-k-(l-1)} \cdot \delta _{30} \cdot \lambda _{3}, \end{aligned}$$

where,

$$\begin{aligned} \delta _{30}&= \left\{ \begin{array}{ll} 1,&{}\text { if, } k+(l-1)+(n+1) = c_2 , i+j+(m-1) < c_1\\ 0,&{} \text { otherwise}\\ \end{array}\right. \\ \end{aligned}$$

Appendix 2: Balance Equation

In this appendix the equations needed for calculating the balance equation is given.

$$\begin{aligned} B_{i,j,k,l,m,n}&= \gamma _{(i,j,k,l,m,n)}^{(i+1,j,k,l,m,n)} P(i+1,j,k,l,m)\\&+\, \gamma _{(i,j,k,l,m,n)}^{(i,j+1,k,l,m,n)} P(i,j+1,k,l,m,n) + \gamma _{(i,j,k,l,m,n)}^{(i,j+1,k,l,m+1,n)}\\&P(i,j+1,k,l,m+1,n)+ \gamma _{(i,j,k,l,m,n)}^{(i,j+1,k,l,m,n+1)} P(i,j+1,k,l,m,n+1)\\&+\, \gamma _{(i,j,k,l,m,n)}^{(i,j,k+1,l,m,n)} P(i,j,k+1,l,m,n) \\&+ \,\gamma _{(i,j,k,l,m,n)}^{(i,j,k,l+1,m,n)} P(i,j,k,l+1,m,n)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i-1,j,k,l,m,n)} P(i\!-\!1,j,k,l,m,n) \!+\! \gamma _{(i,j,k,l,m,n)}^{(i,j\!-\! 11,k,l,m,n)} P(i,j \!-\! 1,k,l,m,n)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k,l,m-1,n)} P(i,j-1,k,l,m-1,n)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k,l,m,n-1)} P(i,j-1,k,l,m,n-1) + \gamma _{(i,j,k,l,m,n)}^{(i,j,k-1,l,m,n)}\\&P(i,j,k-1,l,m,n) + \gamma _{(i,j,k,l,m,n)}^{(i,j,k,l-1,m,n)} P(i,j,k,l-1,m,n) \\&+\,\gamma _{(i,j,k,l,m,n)}^{(i-1,j,k,l,m+1,n)} P(i-1,j,k,l,m+1,n)+ \\&\gamma _{(i,j,k,l,m,n)}^{(i-1,j,k,l,m+1,n-1)} P(i-1,j,k,l,m+1,n-1)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i-1,j+1,k,l,m,n)} P(i-1,j+1,k,l,m,n)+ \\&\gamma _{(i,j,k,l,m,n)}^{(i-1,j+1,k-1,l,m,n+1)} P(i-1,j+1,k-1,l,m,n+1)\\&+ \,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k,l,m+1,n-1)} P(i,j-1,k,l,m+1,n-1) \\&+\,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k,l,m+1,n-2)} P(i,j-1,k,l,m+1,n-2)\\&+ \,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k+1,1,m,n-1)} P(i,j-1,k+1,l,m,n-1)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i,j-1,k,l,m+1,n)} P(i,j-1,k,l,m+1,n)\\&+\, \gamma _{(i,j,k,l,m,n)}^{(i,j,k,l-1,m,n+1)} P(i,j,k,l-1,m,n+1)\\&+\,\gamma _{(i,j,k,l,m,n)}^{(i,j,k,l-1,m-1,n+1)} P(i,j,k,l-1,m-1,n+1) \end{aligned}$$

$$\begin{aligned} A_{i, j, k, l, m, n}&= \gamma _{(i+1,j,k,l,m,n)}^{(i,j,k,l,m,n)}+ \gamma _{(i+1,j,k,l,m-1,n)}^{(i,j,k,l,m,n)}\\&+ \gamma _{(i+1,j,k,l,m-1,n+1)}^{(i,j,k,l,m,n)}+ \gamma _{(i+1,j-1,k,l,m,n)}^{(i,j,k,l,m,n)}\\&+ \gamma _{(i+1,j-1,k+1,l,m,n-1)}^{(i,j,k,l,m,n)}+\gamma _{(i,j+1,k,l,m,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j+1,k,l,m-1,n)}^{(i,j,k,l,m,n)}+\gamma _{(i,j+1,k,l,m+1,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j+1,k,l,m,n+1)}^{(i,j,k,l,m,n)}+\gamma _{(i,j+1,k,l,m-1,n+1)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j+1,k,l,m-1,n+2)}^{(i,j,k,l,m,n)}+\gamma _{(i,j,k+1,l,m,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j,k+1,l,m,n-1)}^{(i,j,k,l,m,n)}+\gamma _{(i,j,k,l+1,m,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j,k,l+1,m,n-1)}^{(i,j,k,l,m,n)}+\gamma _{(i,j,k,l+1,m+1,n-1)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j+1,k-1,l,m,n+1)}^{(i,j,k,l,m,n)}+\gamma _{(i-1,j,k,l,m,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j-1,k,l,m,n)}^{(i,j,k,l,m,n)}+\gamma _{(i,j-1,k,l,m-1,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j-1,k,l,m,n-1)}^{(i,j,k,l,m,n)}+\gamma _{(i,j,k-1,l,m,n)}^{(i,j,k,l,m,n)}\\&+\gamma _{(i,j,k,l-1,m,n)}^{(i,j,k,l,m,n)} \end{aligned}$$