Outage Probability Gap Between Proactive and Reactive Opportunistic Cognitive Relay Networks

Abstract

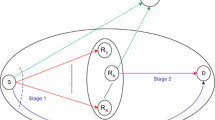
For cognitive relay networks (CRNs) where the secondary link contains multiple relays, considering the interference from primary user (PU) and the maximum transmit power constraint at the secondary user, we investigate the exact and asymptotic outage probabilities for both proactive and reactive decode-and-forward (DF) schemes. Unlike the conventional opportunistic relay networks where the outage probabilities for both proactive and reactive DF schemes are the same, it is found that an outage gap of the two schemes does exist for the CRNs. It is shown that the outage gap tends to zero when the interference caused by PU is high enough and the outage gap increases with the increase of the difference between the threshold signal-to-interference-and-noise ratios at relay and destination.

Appendices

Appendix 1: Proof of Proposition 1

In (6), the CDF of $\text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}})$ can be expressed as

$$\begin{aligned} \text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}})&=\iint _{\varOmega }f_{g_{c r_k}, g_{s r_k}}(x, y)dxdy \end{aligned}$$

(24)

where $\varOmega =\{(x,y)|0<x< \infty , 0<y<\frac{\gamma _{th}^{\mathrm{R}}(\gamma _I x+1)}{\min \{\gamma /g_{sp}, \gamma _{Q}\}}\}$ is the integration region; $f_{X, Y}(\bullet )$ denotes the joint probability density function (PDF) of $X$ and $Y$.

Given $g_{sp}$, both $g_{s {r_k}}$ and $g_{cr_k}$ are exponential RVs in (6). The joint PDF of $g_{c r_k}$ and $g_{s r_k}$ is expressed as

$$\begin{aligned} f_{g_{c r_k},g_{s r_k}}(x, y) =\lambda _{cr}\lambda _{sr}e^{-\lambda _{cr}x-\lambda _{sr}y} \text{ for } x>0, y>0. \end{aligned}$$

(25)

Thus, we have

$$\begin{aligned} \text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}})&=\int _{0}^\infty \lambda _{cr}e^{-\lambda _{cr}x} \int _{0}^{\frac{\gamma _{th}^{\mathrm{R}}(\gamma _I x+1)}{\min \{\gamma /g_{sp}, \gamma _{Q}\}}} \lambda _{sr}e^{-\lambda _{sr}y}dydx \nonumber \\&=1-\lambda _{cr}e^{-\xi }/(\xi \gamma _I+\lambda _{cr}) \end{aligned}$$

(26)

where

$$\begin{aligned} \xi =\frac{\lambda _{sr}\gamma _{th}^{\mathrm{R}}}{\min \{\gamma /g_{sp}, \gamma _{Q}\}}. \end{aligned}$$

(27)

Applying the binomial theorem, we have

$$\begin{aligned} \prod \limits _{r_k \notin {\mathcal {D}}_{l}}\!\!\text{ F }_{\gamma _{s {r_k}}|g_{sp}} (\gamma _{th}^{\mathrm{R}})=\! \sum \limits _{k=0}^{K-l}\! \left( {\begin{array}{c}K-l\\ k\end{array}}\right) \!\! \left( -\frac{\lambda _{cr}e^{-\xi }}{\xi \gamma _I\!+\!\lambda _{cr}}\right) ^{k}. \end{aligned}$$

(28)

Since the PDF of $g_{sp}$ is expressed as

$$\begin{aligned} f_{g_{sp}}(z) =\lambda _{sp}e^{-\lambda _{sp}z} \text{ for } z>0, \end{aligned}$$

(29)

we have

$$\begin{aligned} \alpha =\int _{0}^\infty \sum \limits _{k=0}^{K-l} \left( {\begin{array}{c}K-l\\ k\end{array}}\right) (-1)^k \left( \frac{\lambda _{cr}e^{-\xi }}{\xi \gamma _I+\lambda _{cr}}\right) ^{k+l} \lambda _{sp} e^{-\lambda _{sp}z}dz. \end{aligned}$$

(30)

Since $\min \{\gamma /g_{sp}, \gamma _{Q}\}=\gamma _{Q}$ if $g_{sp}<\gamma /\gamma _{Q}$ and $\min \{\gamma /g_{sp}, \gamma _{Q}\}=\gamma /g_{sp}$ if $g_{sp}\ge \gamma /\gamma _{Q}$, we divide the interval $[0, \infty )$ into two intervals, $[0, \gamma /\gamma _{Q})$ and $[\gamma /\gamma _{Q}, \infty )$. We do the integration over the two intervals respectively. Applying the identity [19, Eq. (3.462.16)], the final result is obtained.

Appendix 2: Proof of Proposition 2

In (7), the CDF of $\text{ F }_{\gamma _{{r_k}d}|g_{cd}}(\gamma _{th}^{\mathrm{D}})$ is obtained as

$$\begin{aligned} \text{ F }_{\gamma _{{r_k}d}|g_{cd}}(\gamma _{th}^{\mathrm{D}})&=\text{ Pr }\left[ \gamma _{{r_k}d}<\gamma _{th}^{\mathrm{D}}\right] \nonumber \\ {}&=\text{ Pr }\left[ g_{r_k d}\!<\!\frac{\gamma _{th}^{\mathrm{D}} (\gamma _I g_{cd}\!+\!1)}{\min \{\gamma /g_{r_kp}, \gamma _{Q}\}}\right] \end{aligned}$$

(31)

Given $g_{cd}$, both $g_{{r_k}d}$ and $g_{{r_k}p}$ are exponential RVs in (7). The PDF of $g_{r_kj}$, $j\in \{d, p\}$, is expressed as

$$\begin{aligned} f_{g_{r_kj}}(x) =\lambda _{rj}e^{-\lambda _{rj}x} \text{ for } x>0. \end{aligned}$$

(32)

Since $\min \{\gamma /g_{r_kp}, \gamma _{Q}\}=\gamma _{Q}$ if $g_{r_kp}<\gamma /\gamma _{Q}$ and $\min \{\gamma /g_{r_k p}, \gamma _{Q}\}=\gamma /g_{r_k p}$ if $g_{r_kp}\ge \gamma /\gamma _{Q}$, we have

$$\begin{aligned} \text{ F }_{\gamma _{{r_k}d}|g_{cd}}(\gamma _{th}^{\mathrm{D}})&= \int _{0}^{\frac{\gamma }{\gamma _{Q}}} \left( 1-e^{-\zeta /\gamma _{Q}}\right) \lambda _{rp} e^{-\lambda _{rp}x}dx \nonumber \\&+\int _{\frac{\gamma }{\gamma _{Q}}}^\infty \left( 1-e^{-\zeta x/\gamma }\right) \lambda _{rp} e^{-\lambda _{rp}x}dx \nonumber \\&= 1-e^{-\zeta /\gamma _{Q}}\left( 1-\frac{\zeta }{\lambda _{rp}\gamma +\zeta } \cdot e^{-\lambda _{rp} \gamma /\gamma _{Q}}\right) \end{aligned}$$

(33)

where

$$\begin{aligned} \zeta =\lambda _{rd}\gamma _{th}^{\mathrm{D}}(\gamma _I g_{cd}+1). \end{aligned}$$

(34)

Thus, we have

$$\begin{aligned}&\prod \limits _{r_k \in {\mathcal {D}}_{l}} \text{ F }_{\gamma _{{r_k}d}|g_{cd}} (\gamma _{th}^{\mathrm{D}})=\left[ \text{ F }_{\gamma _{{r_k}d}|g_{cd}} (\gamma _{th}^{\mathrm{D}})\right] ^l\nonumber \\&\quad =\left[ 1-e^{-\zeta /\gamma _{Q}} \left( 1-\left( 1-\frac{\lambda _{rp}\gamma }{\lambda _{rp}\gamma +\zeta }\right) \cdot e^{-\lambda _{rp} \gamma /\gamma _{Q}}\right) \right] ^l\nonumber \\&\quad =\sum \limits _{i=0}^{l}\!\sum \limits _{j=0}^{i}\!\sum \limits _{m=0}^{j}\!\! \left( {\begin{array}{c}l\\ i\end{array}}\right) \!\!\left( {\begin{array}{c}i\\ j\end{array}}\right) \!\!\left( {\begin{array}{c}j\\ m\end{array}}\right) \!(-1)^{i+j+m} \!\!\left( \!\frac{\lambda _{rp} \gamma }{\zeta \!+\!\lambda _{rp} \gamma }\!\right) ^{\!\!m}\!\!\!e^{-\frac{i\zeta +j\lambda _{rp} \gamma }{\gamma _{Q}}} \end{aligned}$$

(35)

where the second equation is obtained by applying the binomial theorem for three times. Since the PDF of $g_{cd}$ is

$$\begin{aligned} f_{g_{cd}}(x) =\lambda _{cd}e^{-\lambda _{cd}x} \text{ for } x>0, \end{aligned}$$

(36)

we have

$$\begin{aligned} \beta =\int _{0}^\infty \left[ \text{ F }_{\gamma _{{r_k}d}|g_{cd}} (\gamma _{th}^{\mathrm{D}})\right] ^l \cdot \lambda _{cd}e^{-\lambda _{cd}x}dx \end{aligned}$$

(37)

Substituting (35) into (37) and after some mathematical manipulations, the final result is obtained.

Appendix 3: Proof of Theorem 1

Reformulate (5) as follows

$$\begin{aligned} P_{\mathrm{out}}^{\mathrm{react}}&= \text{ E }_{g_{sp}}\text{ E }_{g_{cd}} \left[ \sum \limits _{l = 0}^K \sum \limits _{{\mathcal {D}}_{l}} \prod \limits _{r_k \in {\mathcal {D}}_{l}}(1-\phi '_k) \psi _k\prod \limits _{r_k \notin {\mathcal {D}}_{l}}\phi '_k\right] \end{aligned}$$

(38)

where

$$\begin{aligned} \phi '_k=\text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}}). \end{aligned}$$

(39)

From the binomial theorem, we have

$$\begin{aligned} P_{\mathrm{out}}^{\mathrm{react}}&= \text{ E }_{g_{sp}}\text{ E }_{g_{cd}} \prod \limits _{r_k \in {\mathcal {R}}} \left[ (1-\phi '_k)\psi _k+\phi '_k\right] \nonumber \\&= \text{ E }_{g_{sp}}\text{ E }_{g_{cd}}\prod \limits _{r_k \in {\mathcal {R}}} \left[ (1-\psi _k)\phi '_k+\psi _k\right] \end{aligned}$$

(40)

Employing the binomial theorem, (40) is expressed as

$$\begin{aligned} P_{\mathrm{out}}^{\mathrm{react}}\!=\! \sum \limits _{l = 0}^K \sum \limits _{{\mathcal {D}}_{l}} \text{ E }_{g_{sp}} \!\left[ \prod \limits _{r_k \in {\mathcal {D}}_{l}} \phi '_k\!\right] \! \text{ E }_{g_{cd}}\! \left[ \! \prod \limits _{r_k \in {\mathcal {D}}_{l}}(1-\psi _k)\!\! \prod \limits _{r_k \notin {\mathcal {D}}_{l}}\psi _k\!\right] \end{aligned}$$

(41)

From (16) and (41), we have

$$\begin{aligned} P_{\mathrm{out}}^{\mathrm{proact}}-P_{\mathrm{out}}^{\mathrm{react}}&= \sum \limits _{l = 0}^K \sum \limits _{{\mathcal {D}}_{l}} \text{ E }_{g_{cd}}\!\left[ \! \prod \limits _{r_k \in {\mathcal {D}}_{l}}(1-\psi _k)\!\!\prod \limits _{r_k \notin {\mathcal {D}}_{l}}\psi _k\!\right] \! \nonumber \\&\times \,\, \text{ E }_{g_{sp}} \!\left[ \prod \limits _{r_k \in {\mathcal {D}}_{l}} \text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{D}}) -\text{ F }_{\gamma _{s {r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}})\!\right] \end{aligned}$$

(42)

The function $\text{ F }_{\gamma _{s {r_k}}|g_{sp}}(x)$ is monotonically increasing with respect to $x$. Thus, we obtain the OP relationship of the proactive and reactive DF schemes.

Appendix 4: Proof of Corollary 2

We differentiate $\text{ F }_{\gamma _{s{r_k}}|g_{sp}}(\gamma _{th}^{\mathrm{R}})$ with respect to $\gamma _{th}^{\mathrm{R}}$,

$$\begin{aligned} \frac{\partial \text{ F }_{\gamma _{s{r_k}}|g_{sp}} (\gamma _{th}^{\mathrm{R}})}{\partial \gamma _{th}^{\mathrm{R}}}&\!=\! \frac{\lambda _{sr}\lambda _{cr}e^{-\xi } \left( \frac{\gamma _I}{\xi \gamma _I+\lambda _{cr}}+1\right) }{\lambda _{sr}\gamma _{th}^{\mathrm{R}}\gamma _I\! +\!\lambda _{cr}\min \left\{ \frac{\gamma }{g_{sp}}, \gamma _{\text{ Q }}\right\} }. \end{aligned}$$

(43)

Thus, we have

$$\begin{aligned} \frac{\partial \text{ F }_{\gamma _{s{r_k}}|g_{sp}} (\gamma _{th}^{\mathrm{R}})}{\partial \gamma _{th}^{\mathrm{R}}}>0. \end{aligned}$$

(44)

From (40), we know

$$\begin{aligned} \frac{\partial P_{\mathrm{out}}^{\mathrm{react}}}{\partial \gamma _{th}^{\mathrm{R}}}>0. \end{aligned}$$

(45)

According to (42), the outage gap can be rewritten as

$$\begin{aligned} P_{\mathrm{out}}^{\mathrm{GAP}}= \left\{ \begin{array}{ll} 1-\frac{P_{\mathrm{out}}^{\mathrm{react}}}{P_{\mathrm{out}}^{\mathrm{proact}}}; &{}\text {if }\gamma _{th}^{\mathrm{R}}\le \gamma _{th}^{\mathrm{D}} \\ 1-\frac{P_{\mathrm{out}}^{\mathrm{proact}}}{P_{\mathrm{out}}^{\mathrm{react}}}; &{}\text {if }\gamma _{th}^{\mathrm{R}}>\gamma _{th}^{\mathrm{D}} \end{array}\right. \end{aligned}$$

(46)

Now, the gradient of outage gap is given as

$$\begin{aligned} \frac{\partial P_{\mathrm{out}}^{\mathrm{GAP}}}{\partial \gamma _{th}^{\mathrm{R}}}=\!\! \left\{ \begin{array}{ll} \!\!-\frac{1}{P_{\mathrm{out}}^{\mathrm{proact}}} \cdot \frac{\partial P_{\mathrm{out}}^{\mathrm{react}}}{\partial \gamma _{th}^{\mathrm{R}}}; \!\!&{}\gamma _{th}^{\mathrm{R}}\le \gamma _{th}^{\mathrm{D}} \\ \!\!\frac{P_{\mathrm{out}}^{\mathrm{proact}}}{\left( P_{\mathrm{out}}^{\mathrm{react}}\right) ^2} \cdot \frac{\partial P_{\mathrm{out}}^{\mathrm{react}}}{\partial \gamma _{th}^{\mathrm{R}}}; \!\!&{}\gamma _{th}^{\mathrm{R}}>\gamma _{th}^{\mathrm{D}} \end{array}\right. \end{aligned}$$

(47)

The final result is obtained.