Skip to main content

Advertisement

Springer Nature Link
Log in

Delay Optimization Via Packet Scheduling for Multi-Path Routing in Wireless Networks

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

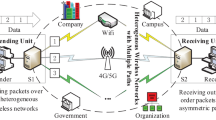
In this paper, the delay optimization problem of multi-path routing in wireless networks is studied. We propose a packet scheduling algorithm weighted shortest delay (WSD) for multi-path routing with the objective minimizing the total weighted delay of a set of packets. To solve the issue of differentiated quality of service, WSD algorithm assigns a nonnegative weight for each packet of every kind of wireless network application. At each network node along the path from source to destination, whenever a link of the node becomes idle, WSD algorithm transmits the packet with largest ratio of its weight to packet length among available packets which have arrived but not yet transmitted. Theoretical analysis proves that WSD algorithm is asymptotically optimal for the total weighted delay of transmitted packets if the arrival times, weights and transmission times of packets are bounded. Real experiment results further verify that WSD algorithm can enhance the delay performance of multi-path routing protocol profoundly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Sharma, G., Mazumdar, R., & Shroff, N. B. D. (2007). Delay and capacity trade-offs in mobile ad hoc networks: A global perspective. IEEE/ACM Transactions on Networking, 15(5), 981–992.

  2. Neely, M. J., & Modiano, E. (2005). Capacity and delay tradeoffs for ad-hoc mobile networks. IEEE Transaction on Information Theory, 51(6), 1917–1937.

    Article  MATH  MathSciNet  Google Scholar 

  3. Belding-Royer, E.M. (2004). Routing approaches in mobile ad hoc networks. In Mobile Ad Hoc Networking, 1(1).

  4. Mueller, S., & Ghosal, D. Multipath routing in mobile ad hoc networks: Issues and challenges, in LNCS Volume 2965/2004.

  5. Marina, M. K., & Das, S. R. (2001). On-demand multipath distance vector routing in ad hoc networks. In Proceedings of the International Conference for Network Procotols.

  6. Gerla, M., & Lee, S. J. (2001). Split multipath routing with maximally disjoint paths in ad hoc networks. IEEE International Conference on Communications, 10.

  7. Wang, L., Shu, Y., & Dong, M., et al. (2001). Adaptive multipath source routing in ad hoc networks. In Proc. IEEE Conference on Communication, Helsinki, Finland.

  8. Perkins, C. E., & Royer, E. M. (1999). Ad hoc on demand distance vector (AODV) routing. In Proc. of the IEEE Workshop on Mobile Computing Systems and Applications.

  9. Ye, Z., Krishnamurthy, S.V., & Tripathi, S.K. (2003). A framework for reliable routing in mobile ad hoc networks, In Proc. of IEEE INFOCOM.

  10. Li, X., & Cuthbert, L. (2004). A reliable node-disjoint multipath routing with low overhead in wireless ad hoc networks, In Proceeding of MSWIM (pp. 4–6), Venezia .

  11. Hou, I.H., Borkar, V., & Kumar, P.R. (2009). A theory of QoS for wireless. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM2009). IEEE Communication Society, 486–694.

  12. Hou, I.H., & Kumar, P.R. (2010). Utility maximization for delay constrained QoS in wireless. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM2010). IEEE Communication Society, 1–9.

  13. Neely, M.J. (2010) Opportunistic scheduling with worst case delay guarantees in single and multi-hop networks. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM2010). IEEE Communication Society, 1728–1736.

  14. Bui, L., Srikant, R., & Stolyar, A. (2009). Novel Architectures and Algorithms for Delay Reduction in Back-pressure Scheduling and Routing. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM2009). IEEE Communication Society, 2936–2940.

  15. Ji, B., Joo, C., & Shroff, N. (2011) Delay-Based Back-Pressure Scheduling in Multi-Hop Wireless Networks. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM2011). IEEE Communication Society, 2579–2587.

  16. Shiang, H. P., & Schaar, M. (2009). Distributed resource management in multihop cognitive radio networks for delay-sensitive transmission. IEEE Transactions On Vehicular Technology, 58(2), 941–953.

    Article  Google Scholar 

  17. Shiang, H. P., & Schaar, M. (2007). Informationally decentralized video streaming over multi-hop wireless networks. IEEE Transactions On Multimedia, 9(6), 1299–1313.

    Article  Google Scholar 

  18. Shiang, H.P., & Schaar, M. (2008) Delay-Sensitive Resource Management in Multi-hop Cognitive Radio Networks. In Proceedings of the IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN2008). IEEE Communication Society, 1–12.

  19. Anderson, E. J., & Potts, C. (2004). Online scheduling of a single machine to minimize total weighted completion time. Mathematics of Operations Research, 29, 686–697.

    Article  MATH  MathSciNet  Google Scholar 

  20. Awerbuch, B., Azar, Y., Leonardi, S., & Regev, O. (1999). Minimizing the flow time without migration. In Proceedings of the 31st Annual ACM Symposium on Theory of Computing (STOC), 198–205.

  21. Bianco, L., & Ricciarddli, S. (1982). Scheduling of a single machine to minimize total weighted completion time subject to release dates. Naval Research Logistics Quarterly, 29, 151–167.

    Article  MATH  Google Scholar 

  22. Chandra, R. (1979). On \(n\) dynamic deterministic problems. Naval Research Logistics Quarterly, 26, 537–544.

    Article  MATH  Google Scholar 

  23. Chandra, C., Sanjeev, K., & Zhu, A. (2001). Algorithms for minimizing weighted flow time. In Proceedings of the 33rd Annual ACM Symposium on Theory of Computing (STOC), 84–93.

  24. Chou, C., Liu, H., Queyranne, M., & Simchi-levi, D. (2006). On the asymptotic optimality of a simple online algotithm for the stochastic single mchine weighted completion time problem and its extensions. Operations Research, 54, 464–474.

    Article  MATH  MathSciNet  Google Scholar 

  25. Chou, C., Queyranne, M., & Simchi-levi, D. (2006). The asymptotic pergormance ratio of an online algorithm for uniform prarllel machine scheduling with release dates. Mathematical Programming, 106, 137–157.

    Article  MATH  MathSciNet  Google Scholar 

  26. Chu, C. (1992). A branch and bound algorithm to minimize total flow time with unequal release dates. Naval Research Logistics, 39, 859–875.

    Article  MATH  MathSciNet  Google Scholar 

  27. Deogun, J. S. (1983). On scheduling with ready times to minimize mean flow time. Computer Journal, 26, 320–328.

    Article  MATH  MathSciNet  Google Scholar 

  28. Dessouky, M. I., & Deogun, J. S. (1981). Sequencing jobs with unequal ready times to minimize mean flow time. SIAM Journal on Computing, 10, 192–202.

    Article  MATH  MathSciNet  Google Scholar 

  29. Dyer, M. E., & Waksey, L. A. (1990). Formulating the single machine sequencing problem with release dates as a mixed integer program. Discrete Applied Mathematics, 26, 255–270.

    Article  MATH  MathSciNet  Google Scholar 

  30. Edmonds, J. (1970). Submodular functions, matroids and certain polyhedra. In Proceedings of the International Conferenceon Cumbinatorics (Calgary Canada),69–87.

  31. Gazmuri, G. (1985). Probabilistic analysis of a machine scheduling problem. Mathematics of Operations Research, 10, 328–339.

    Article  MATH  MathSciNet  Google Scholar 

  32. Goemans, M. X. (1996). A supermodular relaxation for scheduling with release dates, In lecture notes in computer science. Vot 1084. Iroc 5th integer programming and combinatortal optimization conference. 288–300. Berlin: Springer.

  33. Goemans, M. X. (1997). Improved approximation algorithms for scheduling with release dates, In Proceedings of the 8th anmual ACM-SIAM symposium on discrete algorithms. 591–598. Philadelphia: SZAM.

  34. Goemans, M. X., Queyranne, M., & Schulz, A. S. (2002). Single machine scheduling with release dates. SIAM Journal on Discrete Mathematics, 15, 165–192.

    Article  MATH  MathSciNet  Google Scholar 

  35. Hariri, A. M. A., & Potts, C. N. (1983). An algorithm for single machine sequencing with release times to minimize total weighted completion time. Discrete Applied Mathematics, 5, 99–109.

    Article  MATH  Google Scholar 

  36. Kellerer, H., Tautenhahn, T., & Woeginger, G.J. (1996) Approximability and nonapproximability results for minimizing total flow time on a single machine. In ACM Symposium on Theory of Computing (STOC), 418–426.

  37. Lenstra, J. K., Rinnooy Kan, A. H. G., & Brucker, P. (1977). Complexity of machine scheduling problems. Annals of Discrete Mathematics, 1, 343–362.

    MathSciNet  Google Scholar 

  38. Leonardi, S., & Raz, D. (1997) Approximating total flow time on parallel machines. In Proceedings of the 29th Annual ACM Symposium on Theory of Computing, 110–119.

  39. Mohring, R. H., Schulz, A. S., & Uetz, M. (1999). Approximation in stochastic scheduling: the power of LP-based priority policies. Journal of the Association for Computing Machinery (ACM), 46, 924–942.

    Article  MathSciNet  Google Scholar 

  40. Posner, M. E. (1985). Minimizing weighted completion times with deadlines. Operations Research, 33, 562–574.

    Article  MATH  MathSciNet  Google Scholar 

  41. Schulz, A.S. (1966) Scheduling to minimize total. In Proceedings of the 5th international IPCO conferernce on interger programming and conbinatorial optimization, 301–315.

  42. Smith, W. (1956). Various optimizers for single stage production. Naval Research Logistics Quarterly, 3, 59–66.

    Article  MathSciNet  Google Scholar 

  43. Iperf. http://dast.nlanr.net/projects/Iperf.

Download references

Acknowledgments

This work is supported by the National Science Foundation of China under Grant Nos. 61301159, 61273047 and 11471003, the Natural Science Foundation of the Jiangsu Higher Education Institutions of China under Grant No. 13KJB1100188, Chen Guang project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation under Grant No. 13CG18.

Author information

Authors and Affiliations

  1. College of Command Information Systems, PLA Science and Technology University, Nanjing, 210007, China

    Jian Chen & Guyu Hu

  2. School of Electronic Science and Engineering, National Unversity of Defense Technology, Changsha, 410073, China

    Hong Zhang

  3. Department of Information and Communication, Tongji University, Shanghai, 201804, China

    Xinlin Huang

  4. School of Mathematical Science and Institute of Mathematics, Nanjing Normal University, Nanjing, 210023, China

    Xiaoyan Zhang

  5. Faculty of Electrical Engineering, Mathematics and Computer Science, University of Twente, P.O. Box 217, 7500 AE, Enschede, The Netherlands

    Xiaoyan Zhang

Authors
  1. Jian Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hong Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guyu Hu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Xinlin Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Xiaoyan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiaoyan Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, J., Zhang, H., Hu, G. et al. Delay Optimization Via Packet Scheduling for Multi-Path Routing in Wireless Networks. Wireless Pers Commun 82, 2637–2654 (2015). https://doi.org/10.1007/s11277-015-2370-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-015-2370-x

Keywords