Abstract
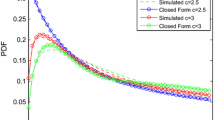
This paper deals with the design of a new system where the channel is subjected to a more generalized scenario by considering two-independent block fading (L = 2). Each block undergoes different fading characteristics for a particular time interval. This time interval is the coherence interval such that the channel coefficient is fixed during a fading block, and statistically independent from one block to another. The main focus of this work is to derive performance measures, such as outage probability and average signal power for Rayleigh, Nakagami, and Weibull fading channels. Once the mathematical expressions are derived, attention is focussed to obtain numerical results for L = 2 by plotting analytical graphs for the obtained expressions and are observed with proposed system parameters like average fading channel power and signal-to-noise ratio (SNR) in the case of a Rayleigh fading channel, Nakagami fading parameter m, fading power Ω, and SNR in the case of a Nakagami fading channel, and Weibull fading parameters k and λ in the case of a Weibull fading channel. The proposed system can thus be evaluated and the amount of degradation can be measured.












Similar content being viewed by others
References
Sklar, B. (2001). Digital communication: Fundamentals and applications (2nd ed.). NJ: Prentice Hall.
Duman, T. M., & Ghrayeb, A. (2007). Coding for MIMO communication systems. England: Wiley.
Rappaport, T. S. (2001). Wireless communications, principles and practice (2nd ed.). NJ: Prentice Hall.
Valluri, B., & Bhaskar, V. (2012). Performance measures over slowly fading MIMO channels using quantised and erroneous feedback. IET Communications, 6(11), 1397–1406.
Knopp, R., & Humblet, P. (2000). On coding for block fading channels. IEEE Transactions on Information Theory, 46(4), 189–205.
Ekbatani, S., Etemadi, E., & Jafarkhani, H. (2009). Throughput maximization over slowly fading channels using quantized and erroneous feedback. IEEE Transactions on Communications, 57(9), 2528–2533.
Papoulis, A., & Pillai, S. U. (2002). Probability, random variables and stochastic processes (4th ed.). NY: Tata McGraw-Hill.
Gradshteyn, I. S., & Ryzhik, I. M. (2000). Table of integrals, series and products (6th ed.). Jamestown Road, London, England: Academic Press.
Steger, C., & Sabharwal, A. (2008). Single-input two-way SIMO channel: Diversity-multiplexing tradeoff with two-way training. IEEE Transactions on Wireless Communications, 7(12), 4877–4886.
Aggarwal, V., & Sabharwal, A. (2008). Performance of multiple access channels with asymptotic feedback. IEEE Journal on Selected Areas in Communications, 26(2), 399–403.
Proakis, J. G. (2001). Digital communications (4th ed.). Singapore: McGraw Hill.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Performance measures like outage probability and average signal power are derived for 3-independent block fading channel (L = 3) as follows:
1.1 Outage Probability
1.1.1 Rayleigh Fading Channel
The outage probability for 3-block Rayleigh fading channel is obtained similarly by substituting L = 3 in (3). It is given as
where
1.1.2 Nakagami Fading Channel
The outage probability for 3-block Nakagami fading channel is obtained similarly by substituting L = 3 in (3). It is given as
where \( u = \frac{{\rho (J_{T} )\Omega }}{m} \), \( K_{1} = \frac{{e^{{\tfrac{1}{u}}} }}{{(\rho (J_{T} ))^{m} \Gamma (m)}}\left( {\frac{m}{\Omega }} \right)^{m} \)
and \( B_{1} = \left( {\frac{{2^{3R} }}{{x_{2} }} - 1} \right) \).
1.1.3 Weibull Fading Channel
The outage probability for a 3-block Weibull fading channel is obtained similarly by substituting L = 3 in (3). It is given as
where \( \mu = \lambda^{2} \rho (J_{T} ) \), \( A = \int\nolimits_{0}^{{t_{\hbox{max} } }} {t^{\nu - 1} } \exp \left( { - t^{\nu } } \right)\left( {\frac{{2^{3R} }}{{x_{1} \left( {t\mu + 1} \right)}} - 1} \right)^{1 + n} dt \), \( t_{\hbox{max} } = \frac{1}{\mu }\left( {\frac{{2^{3R} }}{{x_{1} }} - 1} \right) \), \( t = \frac{{x_{2} - 1}}{\mu }, \), \( \nu = \frac{k}{2} \).
1.2 Average Signal Power
1.2.1 Rayleigh Fading Channel
The average signal power P av for L = 3 is obtained from (17) as
where \( v = \rho (J_{T} )P_{r} \), \( A = \left\{ {\int\nolimits_{1}^{\infty } {\exp \left( {\frac{{ - x_{1} }}{v}} \right)\left[ {\int\nolimits_{1}^{{\tfrac{{2^{3R} }}{{x_{1} }}}} {\left( {\frac{{ - x_{2} }}{v} - \frac{{2^{3R} }}{{x_{1} vx_{2} }}} \right)} dx_{2} } \right]dx_{1} } } \right\} \) and \( B = \int\nolimits_{0}^{1} {\exp } \left( {\frac{{ - 2^{3R} }}{{vx_{1} }} - \frac{{x_{1} }}{v}} \right)dx_{1} \).
1.2.2 Nakagami Fading Channel
The average signal power P av is obtained from (17) as
where \( u = \frac{{\rho (J_{T} )\Omega }}{m} \), \( K_{1} = \frac{{e^{{\tfrac{1}{u}}} }}{{(\rho (J_{T} ))^{m} \Gamma (m)}}\left( {\frac{m}{\Omega }} \right)^{m} \), \( B = \left\{ {1 + u(m - 1)\left( {B_{1} } \right)^{ - 1} + u^{2} (m - 1)(m - 2)\left( {B_{1} } \right)^{ - 2} + \cdots + \left( {B_{1} } \right)^{ - m + 1} u^{m - 1} (m - 1)(m - 2) \ldots (m - (m - 1))} \right\}, \) and \( B_{1} = \left( {\frac{{2^{3R} }}{{x_{2} }} - 1} \right) \).
1.2.3 Weibull Fading Channel
The average signal power P av for L = 3, is obtained from (17) as
where \( \mu = \lambda^{2} \rho (J_{T} ) \), \( A = \int\nolimits_{0}^{{t_{\hbox{max} } }} {t^{\nu - 1} } \exp \left( { - t^{\nu } } \right)\left( {\frac{{2^{3R} }}{{x_{1} \left( {t\mu + 1} \right)}} - 1} \right)^{1 + n} dt \), \( t_{\hbox{max} } = \frac{1}{\mu }\left( {\frac{{2^{3R} }}{{x_{1} }} - 1} \right) \), \( t = \frac{{x_{2} - 1}}{\mu } \), \( \nu = \frac{k}{2} \).
Rights and permissions
About this article
Cite this article
John, R., Bhaskar, V. Analysis of Outage Probability and Average Signal Power of Two Independent Block Fading Channel for a SISO System. Wireless Pers Commun 83, 2051–2068 (2015). https://doi.org/10.1007/s11277-015-2502-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-015-2502-3