Precoding of Space–Time Block Codes for Relay Networks over Correlated MIMO Channels

Abstract

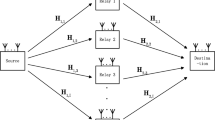
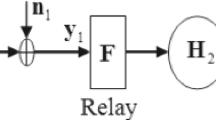
In this paper, we consider the precoder design at both the source and relay nodes of MIMO relay networks to minimize the symbol error rate (SER) based on the statistical channel state information. First compact SER expressions are derived, then the optimization problem of designing the precoding matrices is formulated. This problem is highly nonlinear and nonconvex. We propose a two-step method by exploiting the correlations of the source-relay and relay-destination links. In the first step the two precoding matrices are proved to be in the eigenvector directions of the transmit correlation matrices. In the second step, the original joint problem is decomposed into two independent sub-problems which can be solved in lower complexity. Simulation results show that the precoding system combined with orthogonal space–time block codes (STBC) outperforms the STBC-only system in terms of SER, especially at low signal-to-noise ratios.

Appendices

Appendix 1: Proof of Proposition 1

Proof

A tight approximation for the moment generating function (MGF) of the output SNR is given by [15]

$$ M_{{\tilde{\gamma }_{SNR} }} (s) = M_{{\gamma_{1} }} (s) + M_{{\gamma_{2} }} (s) - M_{{\gamma_{1} }} (s)M_{{\gamma_{2} }} (s) $$

(22)

where the MGF is defined as $M_{{\gamma_{i} }} (s) \triangleq \int_{0}^{\infty } {f_{{\gamma_{i} }} } (\gamma_{i} )e^{{ - s\gamma_{i} }} d\gamma_{i}$. It follows from [7] that ψ _i can be written as the weighted sum of the square of the absolute value of independent complex Gaussian variables. By using the eigen-decomposition of ${\mathbf{L}}_{i}$, the moment generating function of ψ _i is given by$M_{{\psi_{i} }} (s) = \prod\nolimits_{j = 1}^{{M_{i,t} M_{i,r} }} {(1 + \lambda_{j} ({\mathbf{L}}_{i} )s)^{ - 1} = \det ({\mathbf{I}} + {\mathbf{L}}_{i} s)^{ - 1} }$, where $\lambda_{j} ({\mathbf{L}}_{i} )$ is the jth eigenvalue of the positive semi-definite matrix ${\mathbf{L}}_{i}$ for i = 1, 2. M _1,t  = M _S , M _1,r  = M _2,t  = M _R and M _2,r  = M _D are the number of antenna transmitter and receiver respectively. Using (22) and γ _i  = ψ _i /σ ² _i .σ ² _i as shown in (8) and (11), the moment generating function of the approximate $\tilde{\gamma }_{SNR}$ can be calculated as

$$ \begin{aligned} M_{{\tilde{\gamma }_{SNR} }} (s) & = M_{{\psi_{1} }} (s/\sigma_{1}^{2} ) + M_{{\psi_{2} }} (s/\sigma_{2}^{2} ) - M_{{\psi_{1} }} (s/\sigma_{1}^{2} )M_{{\psi_{2} }} (s/\sigma_{2}^{2} ) \\ & = \hbox{det}^{-1} ({\mathbf{I}}_{{M_{S} M_{R} }} + {\mathbf{L}}_{1} s/\sigma_{1}^{2} ) + \hbox{det}^{ - 1} ({\mathbf{I}}_{{M_{R} M_{D} }} + {\mathbf{L}}_{2} s/\sigma_{2}^{2} ) \\ & \quad -\left[ {\det ({\mathbf{I}}_{{M_{S} M_{R} }} + {\mathbf{L}}_{1} s/\sigma_{1}^{2} ) \cdot \det ({\mathbf{I}}_{{M_{R} M_{D} }} + {\mathbf{L}}_{2} s/\sigma_{2}^{2} )} \right]^{ - 1} \\ \end{aligned} $$

(23)

Using the result in (23), the SER of the relay system for both the MPSK and MPAM modulation can be expressed as

$$ \begin{aligned} P_{s} (error) & = \int_{0}^{\infty } {P_{s} \left( {\left. {error} \right|\gamma_{SNR} } \right)} f_{{\gamma_{SNR} }} (\gamma )d\gamma \\ & \approx a\int_{0}^{b\pi } {M_{{\tilde{\gamma }_{SNR} }} (g/\sin^{2} \theta )} d\theta \\ \end{aligned} $$

(24)

Then we can get the approximate expression in (14). The derivation for the MQAM can be done in (15) similarly. This completes the proof of Proposition 1.

Appendix 2: Proof of Proposition 2

Proof

First, the Lemma 1 is helpful for deriving the main result.

Lemma 1

For two non-negative independent random variables x ₁ and x ₂ with x ₁ , x ₂  ∊ (0, 1), the function f(x ₁ , x ₂ ) = x ₁  + x ₂  − x ₁ x ₂ is a monotonically increasing function.

Proof

Take partial derivative of f(x ₁, x ₂)with respect to x ₁ and x ₂, we have $\frac{{\partial f(x_{1} ,x_{2} )}}{{\partial x_{1} }} = 1 - x_{2}$ and $\frac{{\partial f(x_{1} ,x_{2} )}}{{\partial x_{2} }} = 1 - x_{1}$. When x ₁, x ₂ ∊ (0, 1), the function is increasing monotonically. So f(x ₁, x ₂) is minimized when x ₁ and x ₂ are minimized.

Proof of Proposition 2

Let ${\mathbf{X}}_{1} (\theta )$, ${\mathbf{X}}_{2} (\theta )$ be positive definite matrices for arbitrary θ ∊ [θ ₁, θ ₂]. Definite the operator $D({\mathbf{A}})$: return a diagonal matrix whose diagonal elements is consistent with the diagonal elements of original matrix A. For all θ ∊ [θ ₁, θ ₂], it follows from [7] that

$${\text{det}}^{{ - 1}} ({\mathbf{X}}_{1} (\theta )) \ge {\text{det}}^{{ - 1}} (D({\mathbf{X}}_{1} (\theta ))) $$

(25)

$$ {\text{det}}^{{ - 1}} ({\mathbf{X}}_{2} (\theta )) \ge {\text{det}}^{{ - 1}} (D({\mathbf{X}}_{2} (\theta ))) $$

(26)

where the equality is achieved if and only if ${\mathbf{X}}_{1} (\theta )$ and ${\mathbf{X}}_{2} (\theta )$ are diagonal. For ${\text{det}}^{{ - 1}} ({\mathbf{X}}_{1} (\theta ))$ and ${\text{det}}^{{ - 1}} ({\mathbf{X}}_{2} (\theta )) \in \left( {0,1} \right)$, using Lemma 1, we have

$$ f\left[ {{\text{det}}^{{ - 1}} ({\mathbf{X}}_{1} (\theta )),{\text{det}}^{{ - 1}} ({\mathbf{X}}_{2} (\theta ))} \right] \ge f\left[ {{\text{det}}^{{ - 1}} (D({\mathbf{X}}_{1} (\theta ))),{\text{det}}^{{ - 1}} (D({\mathbf{X}}_{2} (\theta )))} \right] $$

(27)

By considering integrals as a sum, the following inequality holds for all θ ∊ [θ ₁, θ ₂] [7].

$$ \int_{{\theta_{1} }}^{{\theta_{2} }} {f\left[ {{\text{det}}^{{ - 1}} ({\mathbf{X}}_{1} (\theta )),{\text{det}}^{{ - 1}} ({\mathbf{X}}_{2} (\theta ))} \right]} d\theta \ge \int_{{\theta_{1} }}^{{\theta_{2} }} {f\left[ {{\text{det}}^{{ - 1}} (D({\mathbf{X}}_{1} (\theta ))),{\text{det}}^{{ - 1}} (D({\mathbf{X}}_{2} (\theta )))} \right]} d\theta $$

(28)

The equality is achieved if and only if ${\mathbf{X}}_{1} (\theta )$ and ${\mathbf{X}}_{2} (\theta )$ are all diagonal matrices. So the SER is minimized when ${\text{det}}^{{ - 1}} (D({\mathbf{X}}_{1} (\theta )))$ and ${\text{det}}^{{ - 1}} (D({\mathbf{X}}_{2} (\theta )))$ are minimized at the same time, and it is equal to that their reciprocals are maximized. Assume that the correlation matrices have the following eigen-decomposition: ${\mathbf{R}}_{i,t} = {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }} \Lambda_{{{\mathbf{R}}_{i,t} }} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{H}$,${\mathbf{R}}_{i,r} = {\mathbf{U}}_{{{\mathbf{R}}_{i.r} }} \Lambda_{{{\mathbf{R}}_{i,r} }} {\mathbf{U}}_{{{\mathbf{R}}_{i,r} }}^{H}$. It follows from [7] that ${\mathbf{L}}_{i}$ in the integral of the SER can be rewritten as

$$ \det ({\mathbf{I}}_{{M_{i,t} M_{i,r} }} + {\mathbf{L}}_{i} g/\sigma_{i}^{2} \sin^{2} \theta ) = \det \left( {{\mathbf{I}}_{{M_{i,t} M_{i,r} }} + (g/\sigma_{i}^{2} \sin^{2} \theta )\left[ {(\Lambda_{{{\mathbf{R}}_{i,t} }}^{1/2} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{T} {\mathbf{W}}_{i}^{ * } {\mathbf{W}}_{i}^{T} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{ * } \Lambda_{{{\mathbf{R}}_{i,t} }}^{1/2} ) \otimes \Lambda_{{{\mathbf{R}}_{i,r} }} } \right]} \right) $$

(29)

where ${\text{det}}^{{ - 1}} ({\mathbf{I}}_{{M_{i,t} M_{i,r} }} + {\mathbf{L}}_{i} g/\sigma_{i}^{2} \sin^{2} \theta ) \in \left( {0,1} \right)$. From (28) and (29), it is seen that the SER is minimized when $\Lambda_{{{\mathbf{R}}_{i,t} }}^{1/2} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{T} {\mathbf{W}}_{i}^{ * } {\mathbf{W}}_{i}^{T} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{ * } \Lambda_{{{\mathbf{R}}_{i,t} }}^{1/2}$ is diagonalized. Therefore the precoding matrices must satisfy

$$ {\mathbf{W}}_{i}^{ * } {\mathbf{W}}_{i}^{T} = {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{ * } {\mathbf{E}}_{{{\mathbf{W}}_{i} }} {\mathbf{E}}_{{{\mathbf{W}}_{i} }}^{T} {\mathbf{U}}_{{{\mathbf{R}}_{i,t} }}^{T} $$

(30)

where ${\mathbf{E}}_{{{\mathbf{W}}_{i} }}$ is a diagonal matrix. So the optimal direction is along the eigenvectors of the transmit correlation matrices. This completes the proof of Proposition 2.

Appendix 3: Proof of Proposition 3

Proof

Since the directions of the precoding matrices have been decided, (29) can be further expressed as follows

$$ \det ({\mathbf{I}}_{{M_{i,t} M_{i,r} }} + {{{\mathbf{L}}_{i} g} \mathord{\left/ {\vphantom {{{\mathbf{L}}_{i} g} {\sigma_{i}^{2} \sin^{2} \theta }}} \right. \kern-0pt} {\sigma_{i}^{2} \sin^{2} \theta }}) = \prod\limits_{m = 1}^{{M_{i,r} }} {\prod\limits_{n = 1}^{{M_{i,t} }} {\left( {1 + (g/\sigma_{i}^{2} \sin^{2} \theta ) \cdot \lambda_{m} ({\mathbf{R}}_{i,r} )\lambda_{n} ({\mathbf{R}}_{i,t} )\lambda_{n} ({\mathbf{P}}_{{{\mathbf{W}}_{i} }} )} \right)} } $$

(31)

We define $g_{{\theta_{i} }} ({\mathbf{W}}_{i} ) \triangleq \prod\limits_{m = 1}^{{M_{i,r} }} {\prod\limits_{n = 1}^{{M_{i,t} }} {\left( {1 + (g/\sigma_{i}^{2} \sin^{2} \theta ) \cdot \lambda_{m} ({\mathbf{R}}_{i,r} )\lambda_{n} ({\mathbf{R}}_{i,t} )\lambda_{n} ({\mathbf{P}}_{{{\mathbf{W}}_{i} }} )} \right)} }$, then (24) can be rewritten as

$$ P_{s} (error) \approx a\int_{0}^{b\pi } {f(g_{{\theta_{1} }}^{ - 1} ({\mathbf{W}}_{1} ),g_{{\theta_{1} }}^{ - 1} ({\mathbf{W}}_{2} ))d\theta } $$

(32)

Notice that (32) is increasing monotonically with θ, so the maximum of integral is achieved when θ is equal to pi/2 for $\forall {\mathbf{W}}_{1} ,{\mathbf{W}}_{2}$.Then the value of SER is equivalent to the special rectangular area as follows

$$ P_{s} (error) = F(\theta_{\hbox{max} } )\Delta \theta $$

(33)

Assuming $g_{{\theta_{i\hbox{max} } }} ({\mathbf{W}}_{i} ) = \prod\nolimits_{m = 1}^{{M_{i,r} }} {\prod\nolimits_{n = 1}^{{M_{i,t} }} {\left( {1 + (g/\sigma_{i}^{2} \sin^{2} \theta_{\hbox{max} } ) \cdot \lambda_{m} ({\mathbf{R}}_{i,r} )\lambda_{n} ({\mathbf{R}}_{i,t} )\lambda_{n} ({\mathbf{P}}_{{{\mathbf{W}}_{i} }} )} \right)} }$, we have $F(\theta_{\hbox{max} } ) = f(g_{{\theta_{1\hbox{max} } }}^{ - 1} ({\mathbf{W}}_{1} ),g_{{\theta_{1\hbox{max} } }}^{ - 1} ({\mathbf{W}}_{2} ))$. Since Δθ is a fixed value, (33) can be replaced with $\hbox{min} P_{s} (error) = \begin{array}{*{20}c} {\hbox{min} } \\ \end{array} F(\theta_{\hbox{max} } )$. From the proof of Proposition 2 we know that $\begin{array}{*{20}c} {\hbox{min} } \\ \end{array} F(\theta_{\hbox{max} } )$ can be converted to $\begin{array}{*{20}c} {\hbox{max} } \\ \end{array} g_{{\theta_{1\hbox{max} } }} ({\mathbf{W}}_{1} )$ and $\hbox{max} g_{{\theta_{2\hbox{max} } }} ({\mathbf{W}}_{2} )$. Because ln (·) is also a monotonically increasing function, so the optimization criteria can be divided into two sub-problems: $\begin{array}{*{20}c} {\hbox{max} } \\ \end{array} \ln g_{{\theta_{1\hbox{max} } }} ({\mathbf{W}}_{1} )$ and $\begin{array}{*{20}c} {\hbox{max} } \\ \end{array} \ln g_{{\theta_{2\hbox{max} } }} ({\mathbf{W}}_{2} )$ under the power constraints.

$$ \begin{array}{*{20}c} {\hbox{max} } \\ \end{array} \ln g_{{\theta_{1\hbox{max} } }} ({\mathbf{W}}_{1} ) = \mathop {\hbox{max} }\limits_{{{\mathbf{W}}_{1} }} \sum\limits_{m = 1}^{{M_{R} }} {\sum\limits_{n = 1}^{{M_{S} }} {\ln \left( {1 + (g/4\sigma_{1}^{2} ) \cdot \lambda_{m} ({\mathbf{R}}_{1,r} )\lambda_{n} ({\mathbf{R}}_{1,t} )\lambda_{n} ({\mathbf{P}}_{{{\mathbf{W}}_{1} }} )} \right)} } $$

(34)

$$ \begin{array}{*{20}c} {\hbox{max} } \\ \end{array} \ln g_{{\theta_{2\hbox{max} } }} ({\mathbf{W}}_{2} ) = \mathop {\hbox{max} }\limits_{{{\mathbf{W}}_{2} }} \sum\limits_{m = 1}^{{M_{D} }} {\sum\limits_{n = 1}^{{M_{R} }} {\ln \left( {1 + (g/4\sigma_{2}^{2} ) \cdot \lambda_{m} ({\mathbf{R}}_{2,r} )\lambda_{n} ({\mathbf{R}}_{2,t} )\lambda_{n} ({\mathbf{P}}_{{{\mathbf{W}}_{2} }} )} \right)} } $$

(35)

This completes the proof of Proposition 3.