Joint Scheduling and Beamforming for Energy Efficiency Maximization in Downlink Coordinated Multi-Cell Networks

Abstract

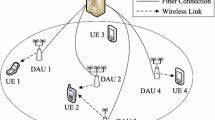
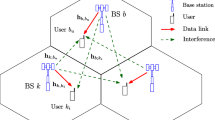
Green communication attracts more and more attention and energy efficiency is becoming an important performance evaluation for the future generations of wireless networks. This paper aims to investigate the optimal energy-efficient design for downlink multi-cell multi-antenna OFDMA environment with coordinated scheduling and beamforming. We target at maximizing the energy efficiency of the whole network subject to the power constraint for each base station and the maximum co-channel interference limitation. At the solving stage, we propose an improved binary search approach (IBSA) which is superlinear convergent and can provide explicit optimal range at every iteration. A joint scheduling and beamforming algorithm is further developed to solve the secondary problem embedded in each iteration of IBSA. Simulation results demonstrate that the proposed algorithm has fast convergent rate and achieves significant performance gain in energy efficiency for cellular network.

Appendices

Appendix 1

Theorem 2

The proposed IBSA is superlinear convergent.

Proof

First, let $\{{q_i}\}$ indicate the sequence generated by IBSA. According to the relative position with ${q^*}$, $\{{q_i}\}$ can be decomposed into three subsequences: $\{ q_j^a\}$ consisting of the elements satisfying $f({q_i})>0$, $\{ q_j^b\}$ consisting of the elements satisfying $f({q_{i - 1}})<0$ and $f({q_i})<0$, $\{ q_j^c\}$ consisting of the rest of elements. From the above definition, if ${q_i}$ pertains to $\{q_j^c\}$, ${q_{i - 1}}$ pertains to $\{ q_j^a\}$ and ${q_{i + 1}}$ pertains to $\{ q_j^a\}$ or $\{ q_j^b\}$.

Next, we will prove the superlinear convergence of subsequence $\{ q_j^a\}$. For $q_j^a < {q^*},\forall j$, we can resort to the conclusion in [23] and obtain

$$\begin{aligned} \frac{{{q^*} - {{R({\mathcal {W}^j},{\mathcal {X}^j})} \big / {{P_T}\left( {\mathcal {W}^j},{\mathcal {X}^j}\right) }}}}{{{q^*} - q_j^a}} \leqslant \left( 1 - \frac{{{P_T}({\mathcal {W}^*},{\mathcal {X}^*})}}{{{P_T}({\mathcal {W}^j},{\mathcal {X}^j})}}\right) , \end{aligned}$$

(30)

where $\{{\mathcal {W}^j}, {\mathcal {X}^j}\}$ is the optimal solution of (11) with $q = q_j^a$. From the mechanism of IBSA, we have ${{R({\mathcal {W}^j},{\mathcal {X}^j})} \big /{{P_T}({\mathcal {W}^j},{\mathcal {X}^j})}} < q_{j + 1}^a$, and furthermore obtain

$$\begin{aligned} \frac{{{q^*} - q_{j + 1}^a}}{{{q^*} - q_j^a}} < \left( 1 - \frac{{{P_T}({\mathcal {W}^*},{\mathcal {X}^*})}}{{{P_T}({\mathcal {W}^j},{\mathcal {X}^j})}}\right) . \end{aligned}$$

(31)

The optimal range gets smaller as algorithm continues, and $q_j^a \rightarrow {q^*}$ as $j\rightarrow \infty$. Since f(q) is continuous and $-{P_T}(\mathcal {W},\mathcal {X})$ is gradient of f(q), it can be easily observed that ${P_T}({\mathcal {W}^j},{\mathcal {X}^j}) \rightarrow {P_T}({\mathcal {W}^*},{\mathcal {X}^*})$ as $q_j^a \rightarrow {q^*}$. Thus, $({{{q^*} - q_{j + 1}^a)} \big / {({q^*} - q_j^a}}) \rightarrow 0$ as $j\rightarrow \infty$.This completes the superlinear convergence proof for $\{ q_j^a\}$. Now we turn to the superlinear convergence proof for $\{q_j^b\}$.

Assume $q_{j + 1}^b = {q_i}$, we have ${q^*} < {q_i} < {q_{i - 1}} \leqslant q_j^b$ from the definition of $\{q_j^b\}$, and

$$\begin{aligned} \frac{{q_{j + 1}^b - {q^*}}}{{q_j^b - {q^*}}} \leqslant \frac{{{q_i} - {q^*}}}{{{q_{i - 1}} - {q^*}}} \leqslant \frac{{{q_i} - {q^l}(i)}}{{{q_{i - 1}} - {q^l}(i)}} \leqslant \frac{{{q_i} - {q^l}(i)}}{{{q^u}(i) - {q^l}(i)}} = \frac{1}{{\varepsilon (i)}}. \end{aligned}$$

(32)

Since $i\rightarrow \infty$ as $j\rightarrow \infty$ and $\varepsilon (\infty ) = \infty$, we have $({{q_{j + 1}^b - {q^*})}\big / {(q_j^b - {q^*}}}) \rightarrow 0$ as $j\rightarrow \infty$.

A subsequence $\{{\hat{q}_k}\}$ of $\{ {q_i}\}$ generated by IBSA can be constructed like this: if ${\hat{q}_k} = {q_i}$, ${\hat{q}_{k + 1}} = {q_{i + 1}}\;or\;{q_{i + 2}}$. This subsequence can be decomposed into $\{ q_j^a\}$ and $\{ q_j^b\}$, each of which converges superlinearly to ${q^*}$ from below and above respectively. Therefore, the sequence generated by IBSA substantially is constitutive of two subsequences with superlinear convergent property and the theorem 2 is proved.

Appendix 2

Theorem 3

Let the initial interval ${q^u}(1) - {q^l}(1) = L$, the value range obtained by IBSA after m iterations satisfies

$$ q^{u} (m) - q^{l} (m) \le L \cdot {{\prod\limits_{{t = 1}}^{m} {\left[ {\varepsilon (t - 1) - 1} \right]} } \mathord{\left/ {\vphantom {{\prod\limits_{{t = 1}}^{m} {\left[ {\varepsilon (t - 1) - 1} \right]} } {\prod\limits_{{t = 1}}^{m} {\varepsilon (t - 1)} }}} \right. \kern-\nulldelimiterspace} {\prod\limits_{{t = 1}}^{m} {\varepsilon (t - 1)} }}{\text{ }} $$

(33)

where ${q^u}(m)$ and ${q^l}(m)$ are the upper and lower bound obtained in the m th iteration.

Proof

The proof should be considered under the following four conditions covering all the possible cases.

• 1. If $f({q_{i - 2}}) < 0$ and $f({q_{i - 1}}) < 0$, that is, ${q_{i - 1}} \in \{ {q_j^b}\}$. From the process of Algorithm 1, we have

  $$\begin{aligned} {q_{i - 1}} = \frac{1}{{\varepsilon (i - 1)}}{q^u}(i - 1) + \frac{{\varepsilon (i - 1) - 1}}{{\varepsilon (i - 1)}}{q^l}(i - 1). \end{aligned}$$

  (34)

  Since ${q^l}(i) = {q^l}(i - 1)$ and ${q^u}(i) = i({q^l}(i - 1),{q_{i - 1}})$, we obtain

  $$\begin{aligned} {q^u}(i) - {q^l}(i) \leqslant {q_{i - 1}} - {q^l}(i - 1) = \frac{1}{{\varepsilon (i - 1)}}({q^u}(i - 1) - {q^l}(i - 1)). \end{aligned}$$

  (35)

  The same procedure may be easily adapted to obtain the other three conclusions.

• 2. If $f({q_{i - 2}}) < 0$ and $f({q_{i - 1}}) > 0$, then ${q^u}(i) - {q^l}(i) \leqslant \frac{{\varepsilon (i - 1) - 1}}{{\varepsilon (i - 1)}}({q^u}(i - 1) - {q^l}(i - 1))$.

• 3. If $f({q_{i - 2}}) > 0$ and $f({q_{i - 1}}) < 0$, that is, ${q_{i - 1}} \in \{ {q_j^c}\}$, then ${q^u}(i) - {q^l}(i) \leqslant \frac{{\varepsilon (i - 1) - 1}}{{\varepsilon (i - 1)}}({q^u}(i - 1) - {q^l}(i - 1))$.

• 4. If $f({q_{i - 2}}) > 0$ and $f({q_{i - 1}}) > 0$, then ${q^u}(i) - {q^l}(i) \leqslant \frac{1}{{\varepsilon (i - 1)}}({q^u}(i - 1) - {q^l}(i - 1))$.

Since $\varepsilon (t) \ge 2$, the maximum upper bound of ${q^u}(m) - {q^l}(m)$ is $L \cdot \prod \nolimits _{t = 1}^m {[{{(\varepsilon (t - 1) - 1)} / {\varepsilon (t - 1)}}]}$, which achieves as case ii and iii happens alternately. This completes the proof.