A Fair Power Splitting Algorithm for Simultaneous Wireless Information and Energy Transfer in CoMP Downlink Transmission

Abstract

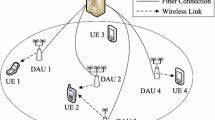
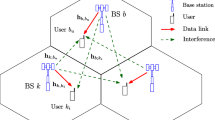
A power splitting approach for simultaneous wireless information and energy transfer is provided in this paper. We consider coordinated multipiont downlink transmission with M base stations (BSs) and J mobile stations (MSs). The main goal of this paper is to maximize per-MS data rate and receiving energy by dynamically optimizing transmitting beamformer. To improve fairness, this problem can be formulated to maximize the minimum rate of all J MSs with per-BS transmitting power constraints and per-MS receiving energy constraints, which is NP-hard problem. Minimum mean square error receiver, affine approximation and alternative convex optimization (ACO) methods are introduced to decompose the original NP-hard problem to several convex subproblems which can be solved by second-order cone programming with low rank (which is equal to the number of data streams) solutions, and then a fast heuristic algorithm is provided to solve the original problem. Numerical results show that the proposed algorithm can achieve fairness, and outperforms sum rate scheme in terms of fairness and outage probability. The fast convergency also demonstrates the proposed algorithm’s good performance.

Appendices

Appendix 1: Proof of Theorem 1

Since (26a) and (26c) are affine objective and constraint, respectively, we only have to represent the rest constraints (26b) and (26d). By introducing slack variables $q_{j,m}, \forall j \in \mathcal {J}, m\in \mathcal {M}$, (26d) is equivalent to

$$\begin{aligned} ||{\dot{{\mathbf {\Lambda }}}}^{1/2}_m {\mathbf {v}}_j||^2&\le q_{j,m} \quad\forall j \in \mathcal {J}, m\in \mathcal {M} \end{aligned}$$

(33)

$$\begin{aligned} \sum \limits _{j \in J} q_{j,m}&\le P,\quad \forall m \in \mathcal {M} , \end{aligned}$$

(34)

where (33) can be further rewritten as [29]

$$ \left| \left| \left[ \begin{array}{ccc} 2{\dot{{\mathbf {\Lambda }}}}^{1/2}_m {\mathbf {v}}_j\\ q_{j,m} - 1 \end{array}\right] \right| \right| \le q_{j,m} + 1,\quad\forall j \in \mathcal {J}, m\in \mathcal {M}. $$

(35)

Then, the transformation of (26d) is finished.

Next, the constraint (26b) is equivalent to

$$\bar{E}_j \le \frac{t + \log \det (\bar{W}_j) + 1}{ \bar{W}_j},$$

(36)

then we represent $\bar{E}_j$ as follows:

$$\begin{aligned} \bar{E}_j= & {} 1 + \mu _j{\mathbf {v}}_j^H {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j {\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j - 2 \sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j \\&+\,\mu _j\sum \limits _{i\ne j} ({\mathbf {v}}_i^H {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j {\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_i ) +\,(\mu _j\sigma _j^2 + \sigma _c^2) {\mathbf {a}}_j {\mathbf {a}}_j^H \\= & {} 1 + ||\sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j - \mu _j{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j||^2 \\&-\mu _j{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j (\mu _j{\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j {\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j)^{-1}{\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j \\&+\,\mu _j\sum \limits _{i\ne j} || {\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_i||^2 + (\mu _j\sigma _j^2+\sigma _c^2) {\mathbf {a}}_j {\mathbf {a}}_j^H \\= & {} ||\sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j - \mu _j{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j||^2 + \sum \limits _{i\ne j} || \sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_i||^2 \\&+\,(\mu _j\sigma _j^2+\sigma _c^2) {\mathbf {a}}_j {\mathbf {a}}_j^H . \end{aligned}$$

(37)

Similar to the case in (26d), by introducing slack variables $\zeta _{j,i}, \forall j,i \in \mathcal {J}$, equation (36) is equivalent the following equations:

$$ ||\sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j - \mu _j{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j||^2 \le \zeta _{j,j}, \quad\forall j \in \mathcal {J} $$

(38)

$$ || \sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_i||^2 \le \zeta _{j,i},\quad \forall i \ne j $$

(39)

$$ \sum \limits _{\forall i \in \mathcal {J}} \zeta _{j,i} \le \frac{t + \log \det (\bar{W}_j) + 1}{ \bar{W}_j} - (\mu _j\sigma _j^2+\sigma _c^2) {\mathbf {a}}_j {\mathbf {a}}_j^H ,\quad \forall j \in \mathcal {J}. $$

(40)

where (38) and (39) can be further rewritten as

$$ \left| \left| \left[ \begin{array}{ccc} 2(\sqrt{\mu _j}{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_j - \mu _j{\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\dot{{\mathbf {H}}}}_j^H {\mathbf {a}}_j)\\ \zeta _{j,j} - 1 \end{array}\right] \right| \right| \le \zeta _{j,j} + 1,\quad\forall j \in \mathcal {J} $$

(41)

$$\left| \left| \left[ \begin{array}{ccc} 2( \sqrt{\mu _j} {\mathbf {a}}_j^H {\dot{{\mathbf {H}}}}_j {\mathbf {v}}_i)\\ \zeta _{j,i} - 1 \end{array}\right] \right| \right| \le \zeta _{j,i} + 1,\quad\forall i \ne j. $$

(42)

Appendix 2: Proof of Corollary 1

Letting $\mu _j = \gamma _j^2, \forall j \in \mathcal {J}$ and then $\bar{E}_j$ can be rewritten as follows

$$ \bar{E}_j = ||F_j^{\frac{1}{2}}\gamma _j - F_j^{-\frac{1}{2}}Y_{j,j}^{\frac{1}{2}}||^2 + \sigma _c^2 {\mathbf {a}}_j {\mathbf {a}}_j^H - Y_{j,j}F_j^{-1}. $$

(43)

After substituting it to the first constraint of (30), we have

$$ ||F_j^{\frac{1}{2}}\gamma _j - F_j^{-\frac{1}{2}}Y_{j,j}^{\frac{1}{2}}||^2 \le L_j, $$

(44)

and finally we can get

$$ \ \ \left| \left| \left[ \begin{array}{ccc} 2(F_j^{\frac{1}{2}}\gamma _j - F_j^{-\frac{1}{2}}Y_{j,j}^{\frac{1}{2}})\\ L_j-1 \end{array}\right] \right| \right| \le L_j+1, \forall j\in \mathcal {J}. $$

(45)

It is easy to transform the second constraint of (30) by $\gamma ^2 <= N_j$ and then reformulate it as follows:

$$ \left| \left| {\left[ \begin{array}{c} 2(\gamma _j)\\ N_j - 1 \end{array}\right] }\right| \right| \le N_j+1 \quad \gamma _j \in [0,1], \forall j \in \mathcal {J}. $$

(46)