Skip to main content
Springer Nature Link
Log in

Exact Closed-Form Expression for End-to-End Average SNR of Dual-Hop Amplify-and-Forward in Wireless Relaying Systems

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

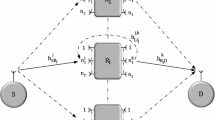
In this paper, we investigate the end-to-end average signal-to-noise ratio (SNR) of dual-hop amplify-and-forward wireless communication systems operating over independent but not necessarily identically distributed (i.n.i.d.) \(\eta {-}\mu \) fading channels. Specifically, we derive a novel exact closed-form expression for the generalized end-to-end average SNR for arbitrary fading parameters \(\eta \) and \(\mu \). Using the obtained closed-form expression for the generalized end-to-end average SNR, some important performance metrics such as the average end-to-end SNR, the amount of fading and the channel capacity can be easily obtained. The effect of the fading parameters and the power imbalance on the overall system performance is investigated. The analytical results are validated by means of Monte-Carlo simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Hasna, M. O., & Alouini, M. (2004). A performance study of dual-hop transmissions with fixed gain relays. IEEE Transactions on Wireless Communications, 3(6), 1963–1968.

    Article  Google Scholar 

  2. Ikki, S. S., & Ahmed, M. H. (2009). Exact error probability and channel capacity of the best-relay cooperative-diversity networks. IEEE Signal Processing Letters, 16(12), 1051–1054.

    Article  Google Scholar 

  3. Al-Qahtani, F. S., Duong, T. Q., Zhong, C., Qaraqe, K. A., & Alnuweiri, H. M. (2011). Performance analysis of dual-hop AF systems with interference in nakagami-m fading channels. IEEE Signal Processing Letters, 18(8), 454–457.

    Article  Google Scholar 

  4. Ikki, S. S., & Aïssa, S. (2012). Performance evaluation and optimization of dual-hop communication over nakagami-m fading channels in the presence of co-channel interferences. IEEE Communications Letters, 16(8), 1149–1152.

    Article  Google Scholar 

  5. Soliman, S. S., & Beaulieu, N. C. (2012). Exact analysis of dual-hop AF maximum end-to-end SNR relay selection. IEEE Transactions on Communications, 60(8), 2135–2145.

    Article  Google Scholar 

  6. Badarneh, O. S., Kadoch, M. (2012). Performance analysis of dual-hop systems with fixed-gain relays over generalized \(\eta {-}\mu \) fading channels, In 2012 IEEE global communications conference, GLOBECOM 2012, Anaheim, December 3–7, 2012 (pp. 4148–4152).

  7. Zhong, C., Matthaiou, M., Karagiannidis, G. K., & Ratnarajah, T. (2011). Generic ergodic capacity bounds for fixed-gain AF dual-hop relaying systems. IEEE Transactions on Vehicular Technology, 60(8), 3814–3824.

    Article  Google Scholar 

  8. Yacoub, M. D. (2007). The \(\kappa {-}\mu \) distribution and the \(\eta {-}\mu \) distribution. IEEE Antennas and Propagation Magazine, 49(1), 68–81.

    Article  Google Scholar 

  9. Prudnikov, A. P., Brychkov, Y. A., & Marichev, O. I. (1990). Integrals, and series: More special Functions. New York: plus Gordon and Breach Science and Publications.

    MATH  Google Scholar 

  10. Papazafeiropoulos, A. K., & Kotsopoulos, S. A. (2011). The \(\alpha {-}\lambda {-}\mu \) and \(\alpha {-}\eta {-}\mu \) small-scale general fading distributions: A unified approach. Wireless Personal Communications, 57, 735–751.

    Article  Google Scholar 

  11. Papazafeiropoulos, A.K., Kotsopoulos, S. A., Zevgolis, D. (2009). “The \(\alpha {-}\lambda {-}\mu {-}\eta \): a general fading distribution,” In 2009 IEEE wireless communications and networking conference, WCNC 2009, proceedings, Budapest, Hungary, April 5–8, 2009 (pp. 404–409).

  12. Prudnikov, A. P., Brychkov, Y. A., & Marichev, O. I. (1992). Integrals, and series: Direct laplace transforms (Vol. 4). New York: Gordon and Breach Science Publishers.

    MATH  Google Scholar 

  13. Mathai, A., & Saxena, R. (1978). The H-function with applications in statistics and other disciplines. New York: Iley Eastern, New Delhi, and Halsted Press.

    MATH  Google Scholar 

  14. Peppas, K. P. (2012). A new formula for the average bit error probability of dual-hop amplify-and-forward relaying systems over generalized shadowed fading channels. IEEE Wireless Communications Letters, 1(2), 85–88.

    Article  Google Scholar 

  15. Ansari, I. S., Al-Ahmadi, S., Yilmaz, F., Alouini, M., & Yanikomeroglu, H. (2011). A new formula for the BER of binary modulations with dual-branch selection over generalized-k. IEEE Transactions on Communications, 59(10), 2654–2658.

    Article  Google Scholar 

  16. Win, M. Z., Mallik, R. K., & Chrisikos, G. (2003). Higher order statistics of antenna subset diversity. IEEE Transactions on Wireless Communications, 2(5), 871–875.

    Article  Google Scholar 

  17. Pérez, J., Ibá nez, J., Vielva, L., & Santamaría, I. (2005). Closed-form approximation for the outage capacity of orthogonal STBC. IEEE Communications Letters, 9(11), 961–963.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Electrical Engineering Department, Faculty of Engineering, University of Tabuk, P.O. Box: 741, Tabuk, 71491, Saudi Arabia

    Osamah S. Badarneh

Authors
  1. Osamah S. Badarneh
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Osamah S. Badarneh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Badarneh, O.S. Exact Closed-Form Expression for End-to-End Average SNR of Dual-Hop Amplify-and-Forward in Wireless Relaying Systems. Wireless Pers Commun 86, 1023–1036 (2016). https://doi.org/10.1007/s11277-015-2970-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-015-2970-5

Keywords